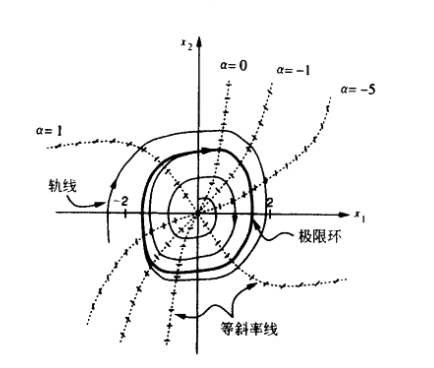
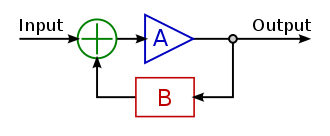
非线性自适应控制器
控制器原理
对于一个系统
x˙=ax2+ux→xd\dot{x}=ax^2+u\\x\rightarrow x_d
x˙=ax2+ux→xd
可以设定 e=xd−xe=x_d-xe=xd−x,并且使 e→0e→0e→0,定义李雅普诺夫函数
V(e)=12e2:PDV(e)=\frac{1}{2}e^2:PD
V(e)=21e2:PD
得到
V˙(e)=ee˙=e(x˙d−ax2−u)\dot{V}(e)=e\dot{e}=e(\dot{x}_d-ax^2-u)
V˙(e)=ee˙=e(x˙d−ax2−u)
要使得上式负定,可以令 e˙=−ke\dot{e}=-kee˙=−ke ,就可以设置 u=x˙d−ax2+keu=\dot{x}_d-ax^2+keu=x˙d−ax2+ke,化简上式为
V˙(e)=−ke2:ND\dot{V}(e)=-ke^2:ND
V˙(e)=−ke2:ND
但是对于上述例子,如果 aaa 是未知的,或者是缓慢变化的数字(a˙=0\dot{a}=0a˙=0)就难以控制,所以需要自适应控制器,可以引入估计值 a^\hat{a}a^ 和估计误差 a~=a−a ...
非线性系统控制器设计
前言
对于一个非线性系统
x˙=f(x,u)\dot{x}=f(x,u)
x˙=f(x,u)
假设 u 是 x 的函数
u=ϕ(x)u=\phi (x)
u=ϕ(x)
反馈线性化
就是将传递函数 f(x,u)f(x,u)f(x,u) 中的非线性部分通过调整 ϕ(x)\phi (x)ϕ(x) 来抵消,最终得到的是一个线性的关系
例子
x˙=f(x,u)=ax2+u\dot{x}=f(x,u)=ax^2+u
x˙=f(x,u)=ax2+u
可以使得 u=ϕ(x)=−ax2−xu=\phi(x)=-ax^2-xu=ϕ(x)=−ax2−x,其中 −ax2-ax^2−ax2 用于抵消系统的非线性量,而 −x-x−x 用于将系统保持平稳,得到
x˙=−x↓x=e−t\dot{x}=-x\\\\
\downarrow\\\\
x=e^{-t}
x˙=−x↓x=e−t
当 t→∞t→\inftyt→∞ 时, x→0x→0x→0
李雅普诺夫直接办法
需要选取李雅普诺夫函数来判断
例子
x˙=f(x,u)=x2−x3+u\dot{x}=f(x,u)=x^2-x^3+u
x˙=f(x,u)=x2−x3+u
...
线性状态观测器和线性控制器综合
前言
对于一个不可观测的系统的控制,就需要用到设计观测器和控制器结合
对于一个系统
X˙=AX+Buy=CX+Du\dot{X}=AX+Bu\\y=CX+Du
X˙=AX+Buy=CX+Du
观测器和控制器设计如下
观测器
根据线性状态观测器的设计
ex˙=(A−LC)exex=X−X^L=[l1l2]\dot{e_x}=(A-LC)e_x\\e_x={X}-{\hat{X}}\\L=\begin{bmatrix}l_1\\l_2\end{bmatrix}
ex˙=(A−LC)exex=X−X^L=[l1l2]
需要 A−LCA-LCA−LC 的特征值小于 0 ,才能使得该误差值逐渐趋近于 0
控制器
其中需要设计控制器为
u=−KX^u=-K\hat{X}
u=−KX^
带入到系统状态方程中可以得到
X˙=AX−BK(X−ex)=(A−BK)X+BKex\dot{X}=AX-BK(X-e_x)=(A-BK)X+BKe_x
X˙=AX−BK(X−ex)=(A−BK)X+BKex
与观测器中的式子合并可以得到
[ex˙x˙]=[A−LC0BKA−BK][exx]=M[e ...
线性控制器设计
系统控制
对于一个开环控制器来说
X˙=AX\dot{X}=AX
X˙=AX
这里的 AAA 的特征值 λ\lambdaλ 决定系统的表现,稳定性
当引入一个输入量时,控制器变为
X˙=AX+Bu\dot{X}=AX+Bu
X˙=AX+Bu
其中由于 uuu 是 XXX 的函数,所以系统形成了一个闭环控制
对于线性控制器来说,输入 uuu 满足
u=−KXu=-KX
u=−KX
代入到控制器中可以得到
X˙=AX−BKX=(A−BK)X\dot{X}=AX-BKX=(A-BK)X
X˙=AX−BKX=(A−BK)X
可以选择 KKK 的数值来使得 XXX 前的系数的特征值 λi\lambda_iλi 处于一个期望的位置上,一般来说,需要保证其特征值均 ≤0≤0≤0 才能使得系统稳定
选取 λi\lambda_iλi 的原则
如果选取 λ\lambdaλ 为虚数,那么一定会有共轭解存在,将一定会引入一个反复的振动
λ\lambdaλ 决定收敛的速度,最后的解的形式会变为 c1eλ1+c2eλ2+...c_1e^{\lambda_1}+c_2e^{\lambda_2}+...c1e ...
线性状态观测器
系统的可观测性
对于一个开环系统
X˙=AXy=CX\dot{X}=AX\\y=CX
X˙=AXy=CX
可以得到系统的状态转移方程
X=eAtX(0)X=e^{At}X(0)
X=eAtX(0)
根据状态方程的解,可以知道
y=CX=CeAtX(0)y=CX=Ce^{At}X(0)
y=CX=CeAtX(0)
根据矩阵质数定义的状态转移矩阵有
eAt=I+At+12!A2t2+...e^{At}=I+At+\frac{1}{2!}A^2t^2+...
eAt=I+At+2!1A2t2+...
取前 n 项
eAt=I+At+12!A2t2+...+1(n−1)!An−1tn−1e^{At}=I+At+\frac{1}{2!}A^2t^2+...+\frac{1}{(n-1)!}A^{n-1}t^{n-1}
eAt=I+At+2!1A2t2+...+(n−1)!1An−1tn−1
带入到上面 y 的式子中
y=(CI+CAt+...+1(n−1)!CAn−1tn−1)X(0)=[It...1(n−1)!tn−1][CCA…CAn−1]X(0)y=(CI+CAt+...+\frac ...
LQR线性二次型调节器
github仓库
线性指的是系统是线性的,典型的线性系统的状态方程
x(k+1)=Ax(k)+Bu(k)x(k+1)=Ax(k)+Bu(k)
x(k+1)=Ax(k)+Bu(k)
二次型是指代价函数 JJJ 是二次型的。
J=12x(N)TSx(N)+12∑k=0N−1[xT(k)Qx(k)+uT(k)Ru(k)]J=\frac{1}{2} x(N)^TSx(N)+\frac{1}{2}\sum_{k=0}^{N-1}{[x^T(k)Qx(k)+u^T(k)Ru(k)]}
J=21x(N)TSx(N)+21k=0∑N−1[xT(k)Qx(k)+uT(k)Ru(k)]
其中前一项中 NNN 表示末端时刻, xdx_dxd 是系统的参考,也就是目标,这个 JJJ 是末端代价, SSS 为末端状态的权重矩阵,是一个对角阵, QQQ 是运行过程中的权重矩阵, RRR 是控制量的权重矩阵, SSS 和 QQQ 是 N×NN\times NN×N 的,但是 RRR 是 P×PP\times PP×P的,如果对某个元素要求大时可以对应的将 RRR 增大,关键的是 SSS 和 QQQ 都是半正 ...
matlab中LMI工具箱使用
初始化一个 LMI 系统
12setlmis(lmi0);setlmis([]); % 常用
向 LMI 系统中添加矩阵变量 lmivar
12X = lmivar(type, struct); % 常用[X, ndec, xdec] = lmivar(type, struct); % ndec表述与X有关的决策变量的个数,xdec表示X对这些决策变量的初始依赖关系
type类型对应的数值
含义
1
对角线对称矩阵格式,每个对角块都是满块
2
矩形块,struct=[m,n] 表示 m x n 阶矩阵
3
描述复杂类型的矩阵
type=1
struct 包含两个基本变量
第一个描述矩阵块的阶数
第二个描述矩阵块的类型
0
标量
1
满块
-1
零块
type=2
type=3
描述复杂类型的矩阵
返回 LMI 的函数的内部描述 getlmis
1lmisys = getlmis % lmisys 称为存储在机器内部线性矩阵不等式系统的名称,一个线性矩阵不等式以 setlmis 开始,以 getlmis 结束 ...
不变性原理
前言
李雅普诺夫的不变性原理(LaSalle’s Invariance Principle,也称为李雅普诺夫-拉塞尔不变性原理)是动力系统和控制理论中用于分析系统长期行为的重要工具。它是对经典李雅普诺夫稳定性理论的扩展,尤其在处理非线性系统时非常有用。
示例
对于一个简单的倒立摆
可以求出系统状态空间方程是
Lϕ¨+gsinϕ=0L\ddot{\phi}+gsin\phi=0
Lϕ¨+gsinϕ=0
设
x=[x1x2]x1=ϕx2=ϕ˙x=\begin{bmatrix}x_1\\x_2\end{bmatrix}\\
x_1=\phi\\
x_2=\dot{\phi}
x=[x1x2]x1=ϕx2=ϕ˙
求导之后可以得到
x˙1=x2x˙2=−gLsinx1\dot{x}_1=x_2\\
\dot{x}_2=-\frac{g}{L}sinx_1
x˙1=x2x˙2=−Lgsinx1
寻找李雅普诺夫函数,可以使用能量方程来求解
E=K+P=12mv2+mgh=12m(Lϕ˙)2+mgL(1−cosϕ)E=K+P\\
=\frac{1}{2}mv^2+mgh=\f ...
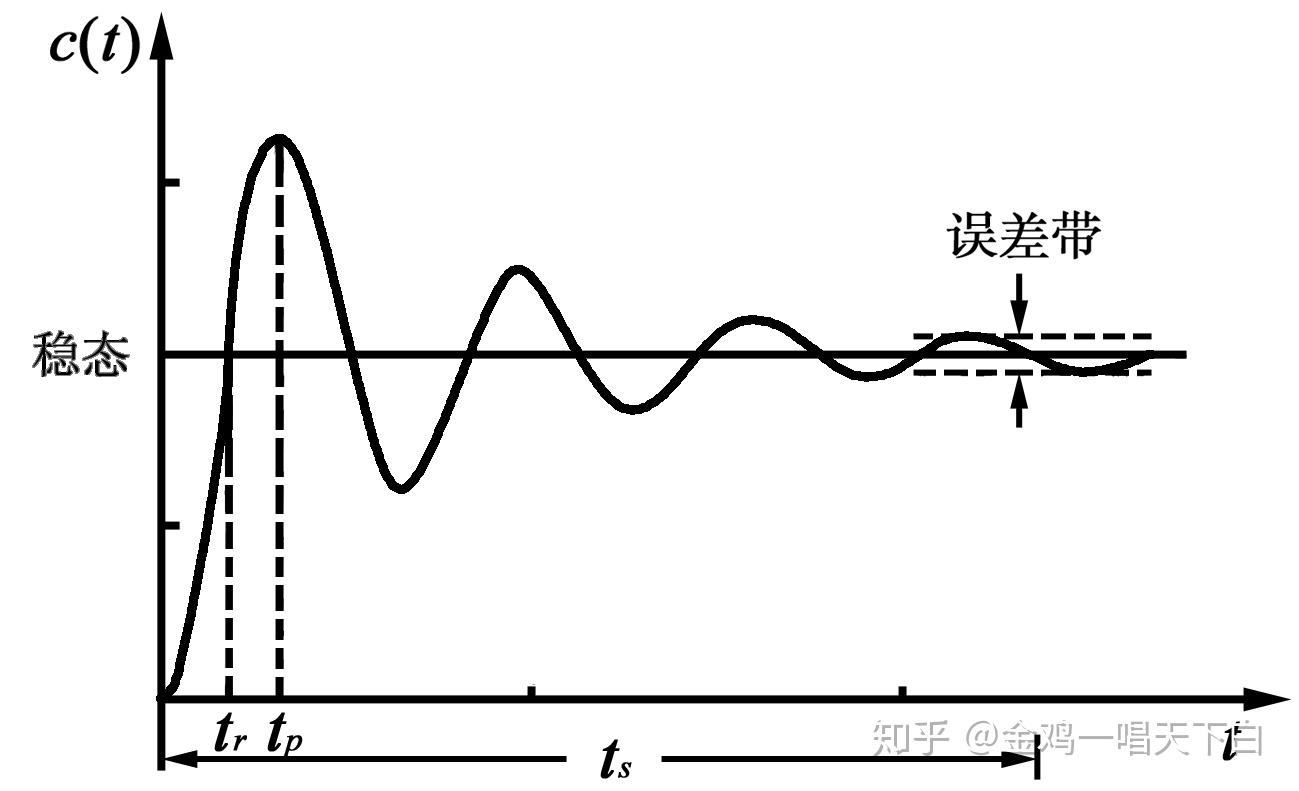
系统的稳定性
前言
稳定性:系统在离开平衡点之后的动态反应随时间不增加
函数的一些知识
PD 正定
V(x)=0 if and only if x=0V(x)=0\ if\ and\ only\ if\ x=0V(x)=0 if and only if x=0
V(x)>0 if and only if x≠0V(x)>0\ if\ and\ only\ if\ x\neq 0V(x)>0 if and only if x=0
PSD 半正定
V(x)=0 if and only if x=0V(x)=0\ if\ and\ only\ if\ x=0V(x)=0 if and only if x=0
V(x)≥0 if and only if x≠0V(x)\geq0\ if\ and\ only\ if\ x\neq 0V(x)≥0 if and only if x=0
ND 负定
V(x)=0 if and only if x=0V(x)=0\ if\ and\ only\ if\ x=0V(x)=0 if and only if x=0
V(x)<0 ...
系统的可控性
对于一个系统状态方程
X˙=AX+Bu\dot{X}=AX+Bu
X˙=AX+Bu
离散型与连续型是一样的
Xk+1=AXk+BukX_{k+1}=AX_k+Bu_k
Xk+1=AXk+Buk
X1=AX0+Bu0X2=AX1+Bu1=A2X0+ABu0+Bu1…Xn=AXn−1+Bun−1=AnX0+An−1Bu0+⋯+ABun−2+Bun−1X_{1}=AX_0+Bu_0\\\\
X_2=AX_1+Bu_1=A^2X_0+ABu_0+Bu_1\\\\
\dots\\\\
X_n=AX_{n-1}+Bu_{n-1}=A^nX_0+A^{n-1}Bu_0+\dots+ABu_{n-2}+Bu_{n-1}
X1=AX0+Bu0X2=AX1+Bu1=A2X0+ABu0+Bu1…Xn=AXn−1+Bun−1=AnX0+An−1Bu0+⋯+ABun−2+Bun−1
转化为矩阵形式
Xn=[BABAn−1BAn][un−1un−2…u0X0]X_n=\begin{bmatrix}B&AB&A^{n-1}B&A^n\end{bmatri ...
Hamilton Matrix and Equation
Hamiltonian Equation
最优化问题求解中的汉密尔顿方程是最优控制方法解决动态优化问题的一阶必要条件
首先看需要解决的问题
max∫t0t1f(x,u)dtx˙=g(x,u)x(t0)=x0x(t1):freemax\int_{t_0}^{t_1}f(x,u)dt\\\\
\dot{x}=g(x,u)\\\\
x(t_0)=x_0\\\\
x(t_1):free
max∫t0t1f(x,u)dtx˙=g(x,u)x(t0)=x0x(t1):free
引入一个函数 λ(t)\lambda (t)λ(t) 表示一个定义在 t0≤t≤t1t_0\leq t\leq t_1t0≤t≤t1 上的连续的可微函数,那么对于任何满足上述约束的 x(t),u(t)x(t),u(t)x(t),u(t) 有
∫t0t1f(x,u)dt=∫t0t1[f(x,u)+λg(x,u)−λx˙]dt\int_{t_0}^{t_1}f(x,u)dt=\int_{t_0}^{t_1}[f(x,u)+\lambda g(x,u)-\lambda \dot{x}]dt
∫t0t1f(x, ...
Riccati方程
前言
群
群就是一种集合加上一种运算的代数结构,把集合记作 AAA ,运算记作 ⋅\cdot⋅ ,那么群就可以记作 G=(A,⋅)G=(A,\cdot)G=(A,⋅) ,一个群满足如下性质
封闭性: ∀a,b∈A,a⋅b∈A\forall a,b\in A,a\cdot b\in A∀a,b∈A,a⋅b∈A
结合律: ∀a,b,c∈A,(a⋅b)⋅c=a⋅(b⋅c)\forall a,b,c\in A,(a\cdot b)\cdot c=a\cdot(b\cdot c)∀a,b,c∈A,(a⋅b)⋅c=a⋅(b⋅c)
单位元 eee : ∃e∈A,∀b∈A,e⋅b=b⋅e=b\exist e\in A,\forall b\in A,e\cdot b=b\cdot e=b∃e∈A,∀b∈A,e⋅b=b⋅e=b
逆元: ∀a∈A,∃a−1∈A,a⋅a−1=a−1⋅a=e\forall a\in A,\exist a^{-1}\in A,a\cdot a^{-1}=a^{-1}\cdot a=e∀a∈A,∃a−1∈A,a⋅a−1=a−1⋅a=e
群结构保证了在群上的运算具有良好的性质
李 ...
矩阵求导和迹运算
求导
对与矩阵 XXX, AAA, UUU, VVV
dXTX=IdXXT=IdXTAX=AdAXXT=AdAXX=ATdXAX=ATdXTXX=2XdXTAXX=(A+AT)XdXTAXXXT=ddX(dXTAXdX)=AT+A∂U∂XT=(∂UT∂X)T∂UTV∂X=∂UT∂XV+∂VT∂XUT∂UVT∂X=∂U∂XVT+U∂VT∂X∂[(XU−V)T(XU−V)]∂X=2(XU−V)UT∂UTXV∂X=UVT∂UTXTXU∂X=2XUUT\frac{dX^T}{X}=I\\\\
\frac{dX}{X^T}=I\\\\
\frac{dX^TA}{X}=A\\\\
\frac{dAX}{X^T}=A\\\\
\frac{dAX}{X}=A^T\\\\
\frac{dXA}{X}=A^T\\\\
\frac{dX^TX}{X}=2X\\\\
\frac{dX^TAX}{X}=(A+A^T)X\\\\
\frac{dX^TAX}{XX^T}=\frac{d}{dX}(\frac{dX^TAX}{dX})=A^T+A\\\\
\frac{\partial U}{\partial X^T} ...
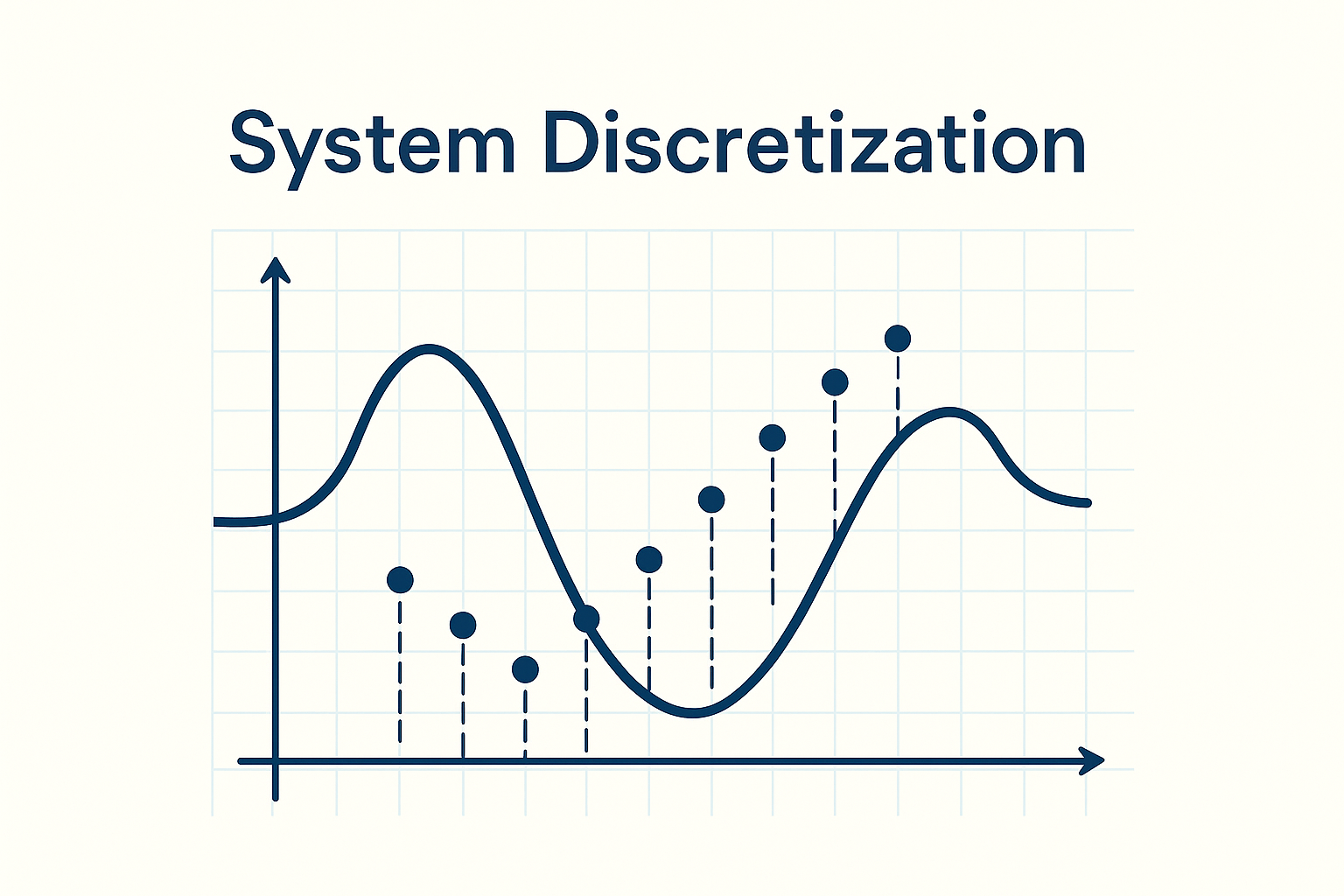
系统离散化
连续时间系统
一般来说系统的状态变化都是连续的
离散时间系统
数字控制器,有时候计算时需要将系统的状态离散化,控制器是离散的输出。这就需要将离散系统和连续系统结合起来,需要用到一些模块。首先是通过ADC将传感器信号采样并转化为离散输出,同时其他的参数都将是离散的形式。随后控制器的输出将会通过DAC转化为连续的系统输出,控制量的输出需要使用到保持器来保证在一个控制周期之内的控制量保持不变。
对于采样,采样频率太快会使数据堆积,需要大量的存储数据,采样频率太小,小于控制周期,会产生误差,采样频率一般采用被采样数据频率的2倍甚至是5-10倍,如果在中断中采样并且处理数据的话,采样周期一定要大于处理所用的时间,否则这段期间内的采样就没有了意义。
有时候会把连续系统近似为离散的系统之后设计算法来控制系统,连续系统与离散系统的转换
采样周期的选取
一般来说肯定是采样周期越小越好 T→0⇒y[k]→y(t)T→0 \Rightarrow y[k]\rightarrow y(t)T→0⇒y[k]→y(t),需要存储大量数据,内存占用多
T↑T\uparrowT↑ 会导致产生混叠,根据采样定理,采样频 ...
传递函数和状态空间方程
状态空间
对于一个系统的状态空间方程,可以使用 Laplace 变换来得到系统的运行状态方程
状态空间方程——一个包含输入,输出,状态变量的集合的一阶微分方程,但是对于高阶的系统,可以选择合适的状态量来消除高阶的系数
根据下式求出的状态空间方程中,对于矩阵 A 的特征值是决定系统极点的位置,可能会决定系统的稳定性
状态空间方程的解
对于一个状态空间方程
{x˙(t)=Ax(t)+Bu(t)y(t)=Cx(t)+Du(t)\left\{\begin{aligned}\dot{x}(t)=Ax(t)+Bu(t)\\y(t)=Cx(t)+Du(t)\end{aligned}\right.
{x˙(t)=Ax(t)+Bu(t)y(t)=Cx(t)+Du(t)
对上述第一个式子求解,可以将状态空间方程的解写作如下的形式,解分为两个部分,第一项为零输入响应,第二项为零状态响应。对于零输入响应,当输入 u(t)=0u(t)=0u(t)=0 时,系统的状态仅由初始状态 X(t0)X(t_0)X(t0) 驱动,其中 eA(t−t0)e^{A(t-t_0)}eA(t−t0) 是矩阵指数。对于零状态响 ...
深入理解计算机系统
快捷键
窗口操作
切换窗口:Alt+Tab
窗口移动:Win+↑/↓/←/→
文件操作
保存:Ctrl+S
关闭文件:Ctrl+W
撤销:Ctrl+Z
恢复:Ctrl+Shift+Z
复制/粘贴:Ctrl+C/V
向上/向下翻页:PageUp/PageDown
切换到左/右边的文件:Ctrl+PageUp/PageDown
选择操作
全选:Ctrl+A
选中:Shift+各种移动/跳转
光标操作
上/下/左/右移动光标:↑/↓/←/→
向上/下插入光标:Ctrl+Alt+↑/↓
在下一个匹配项处插入光标:Ctrl+D
查找/替换匹配项:Ctrl+F/H
全局查找/替换匹配项:Ctrl+Shift+F/H
更改操作
行删除:Shift+Delete
行上/下交换:Alt+↑/↓
跳转操作
跳转到上/下个光标位置:Alt+←/→
跳转到词首/尾:Ctrl+←/→
跳转到行首/尾:Home/End
跳转到列首/尾:Ctrl+Home/End
跳转到行:Ctrl+G
跳转到括号:Ctrl+Shift+
跳到定义:F12
查看定义:Alt+F12
VSCode 其他操作
向右拆分编辑器:Ctrl ...
代码整洁之道
时刻保持初心,保持代码整洁
变量命名规则
名副其实,见名知意
避免误导
做有意义的区分
使用读的出来的名称
使用可以搜索的名称
避免使用编码
成员前缀
匈牙利语标记法
避免思维映射
类名
类名和对象名应该是名词或名词短语
类名不应当是动词
方法名
方法名应当是动词或动词短语
别扮可爱
每个概念对应一个词
别用双关语
使用解决方案领域的名称
给这些事取个技术性的名称,通常是最靠谱的做法。
使用源自所涉问题领域的名称
添加有意义的语境,不要添加没用的语境
函数的定义规则
短小 函数的第一规则是要短小。第二条规则是还要更短小。
只做一件事
每个函数一个抽象层级
switch语句
使用描述性的名称
函数参数
最理想的参数数量是零(零参数函数),其次是一(单参数函数),再次是二(双参数函数),应尽量避免三(三参数函数)。有足够特殊的理由才能用三个以上参数(多参数函数)—所以无论如何也不要这么做。
标识参数丑陋不堪。向函数传入布尔值简直就是骇人听闻的做法。这样做,方法签名立刻变得复杂起来,大声宣布本函数不止做一件事。如果标识为 true 将会这样做,标识为 fals ...
git
前言
git 是一个十分强大的远程项目管理的系统,对于开发者来说十分重要,它的版本管理功能也十分强大,而且存储空间也有 1GB,还算挺大的。
本人曾在一次事故中磁盘损坏导致丢失了自己做的项目,熬夜半年多完成的心血,很心痛。。。
所以在这里告诫大家, 一定要做好备份
SSH与github
SSH(安全外壳协议,Secure Shell 的缩写)是建立在应用层基础上的安全协议。SSH 是目前较可靠,专为远程登录会话和其他网络服务提供安全性的协议,利用 SSH 协议可以有效防止远程管理过程中的信息泄露问题。简单来说,SSH就是保障你的账户安全,将你的数据加密压缩,不仅防止其他人截获你的数据,还能加快传输速度。
一般来说,安装 git bash 之后实际上是自带 SSH 的,所以可以检验一下,在终端输入指令 ssh 会显示出 usage 的内容,那就是装好了,有问题的话,可以自行百度一下。
没问题了就可以输入指令 ssh-keygen -t rsa ,使用 RSA 算法生成密钥,然后,如下
其中 红色圈里面是输入保存的地址,蓝色圈里输入的是 passphrase,可以不输入,直接回车就行。最 ...