VS2022 配置 casadi 求解 NMPC 问题

前言

最近在研究 NMPC 时，找到了 casadi 这个求解库，本来是在 ros+gazebo 平台上搭建的，但是最终的运行效果不太好，所以就打算先使用自己比较熟悉的 webots+vs 平台上进行测试，之后再移植过去

部署优化求解工具 casadi

下载 ipopt 的 vs2022 预编译程序

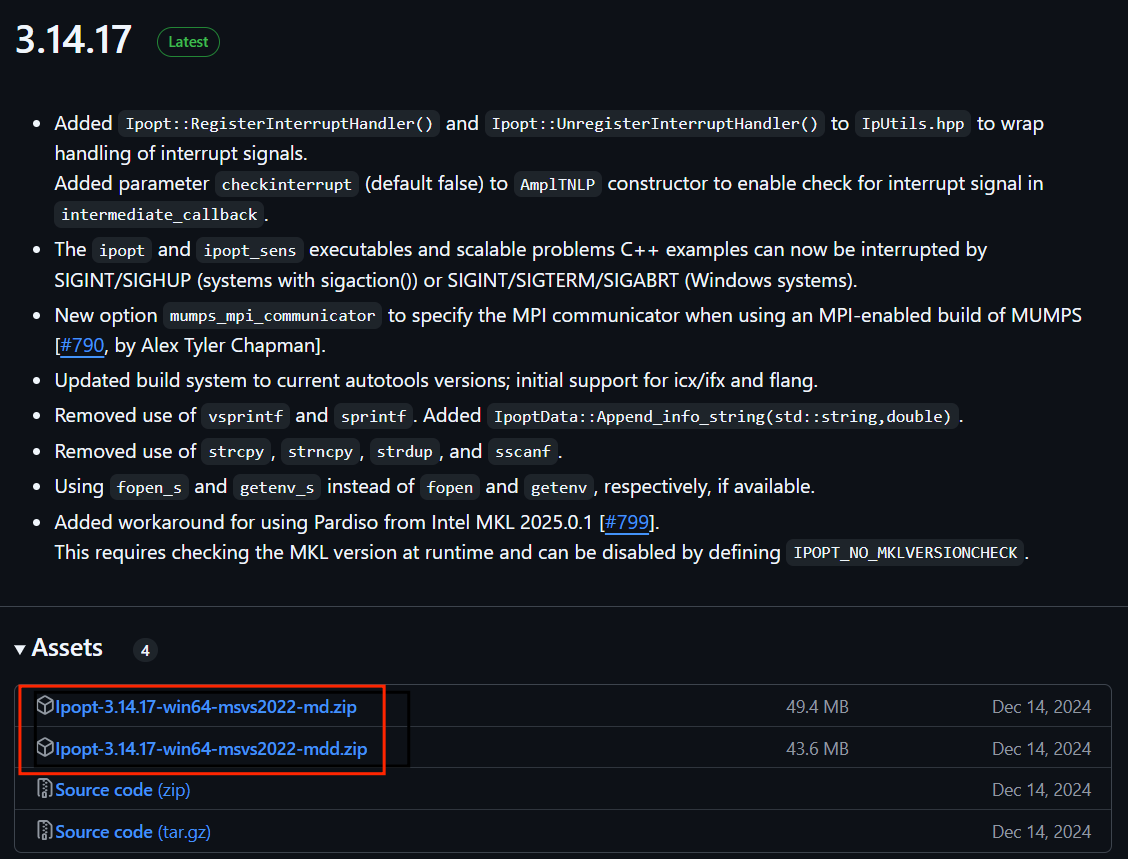
在 ipopt 的 github 官方仓库中找到 vs2022 的预编译版本，就是基于 vs2022 已经编译好的，不需要自行编译。可以直接选择较新的版本，记得要选择后面带有 msvs2022 的压缩包

下载 casadi 的源码

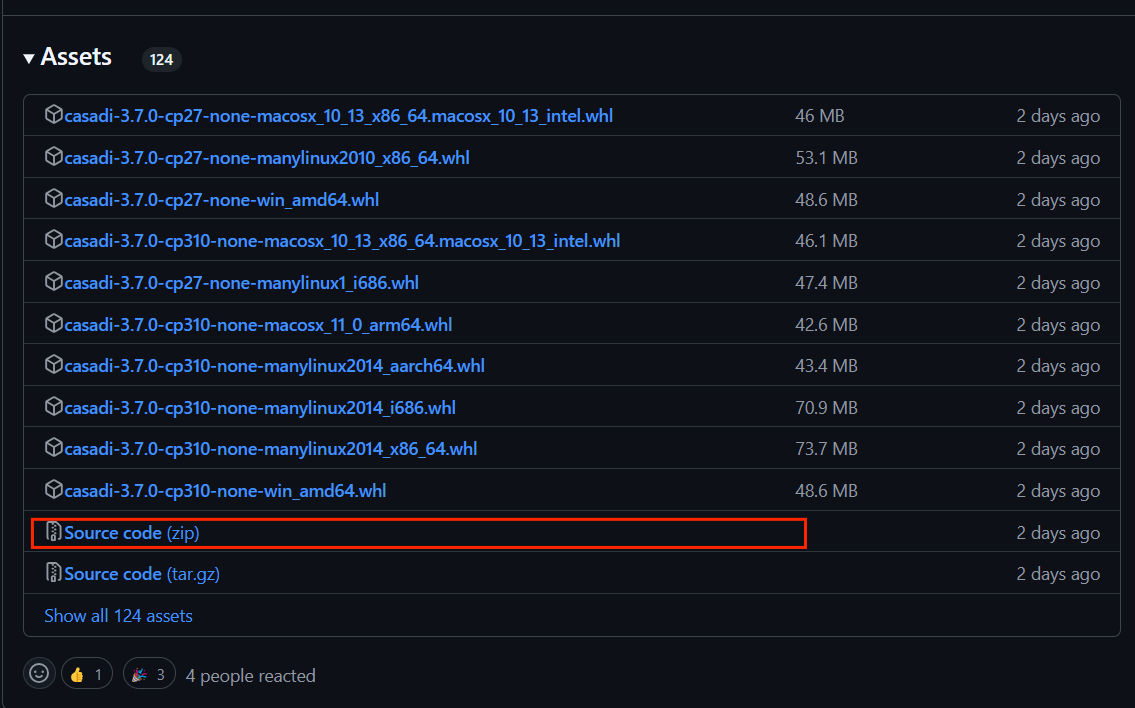
在 casadi 的 github 官方仓库中找到适合的版本，下载对应的 Source Code 压缩包即可

编译

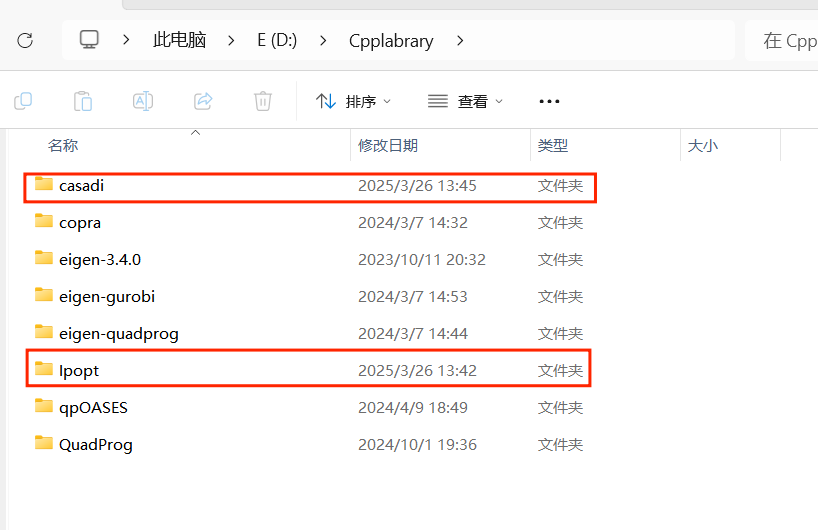
由于下载的 ipopt 不需要编译，所以就只需要编译 casadi 即可。把上述的 ipopt 和 casadi 的源码放到一个不会被删掉的地方，建议是有一个比较统一存放 C++ 依赖库的地方，如下图所示

然后在 casadi 的目录下新建一个 install 目录下，并且在 casadi 目录下新建一个 run.bat 文件，这个文件中需要写入 casadi 的编译和安装脚本，但是一般双击 .bat 文件时会直接运行，所以可以先新建一个 run.txt 文件，之后再重命名即可。在文件中写入如下指令

cmake -G "Visual Studio 17 2022" -A x64 -B build -DWITH_IPOPT=ON -DIPOPT_LIBRARIES:FILEPATH="ipopt的目录/lib/ipopt.dll.lib" -DIPOPT_INCLUDE_DIRS:PATH="ipopt的目录/include/coin-or"  -DCMAKE_INSTALL_PREFIX:PATH="casadi的目录/install"
cmake --build build --config Release
cmake --install build

之后双击运行，等待其编译安装结束

在 vs 中配置 casadi

编译完成之后需要在 vs2022 的 IDE 中进行配置。由于这个配置是针对于项目的，所以可以做一个属性表，就能够重复利用到多个项目中

制作属性表

打开一个项目，并且在项目中打开 视图-其他窗口-属性管理器，在属性管理器中添加新新项目属性表

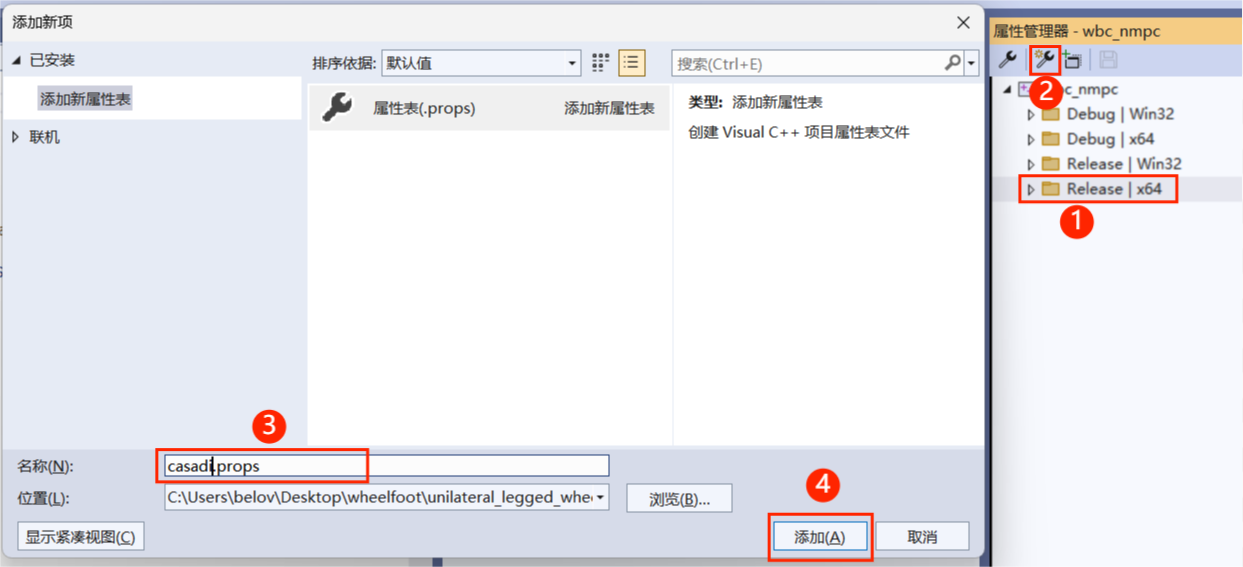
就可以看到在 Release x64 下有个 casadi 的配置，然后右键打开其属性，开始编辑属性

包含目录

位于 VC++ 目录下，在其中添加新项目，如下

casadi存放目录\install\casadi\include
casadi存放目录\install\casadi

外部包含目录

位于 VC++ 目录下，在其中添加新项目

casadi存放目录\install\casadi
casadi存放目录\install\casadi\include

库目录

位于 VC++ 目录下，在其中添加新项目

casadi存放目录\build\Release
casadi存放目录

附加库目录

位于链接器-常规下，在其中添加新项目，如下

casadi存放目录\casadi\core\runtime
casadi存放目录\casadi\core
casadi存放目录\build\casadi\core
casadi存放目录\build
casadi存放目录

附加依赖项

位于链接器-输入下，在其中添加新项目，如下

casadi.lib

到此属性表就制作完毕了，之后就可以选中对应的属性表，右键保存之后就可以在该项目的目录下看到这个 casadi.props 文件。在之后的使用中就直接把这个文件复制到对应的项目目录下，在该项目的属性管理器中导入该属性表即可。需要注意的是，如果你的依赖库的位置发生了改变，属性表也需要改变

添加动态链接库文件

动态链接库 dll 文件是运行 exe 文件时实时调用的，因此需要将dll文件复制粘贴到生成的 exe 文件同级目录，将编译生成的 casadi.dll 以及 casadi_nlpsol_ipopt.dll 文件粘贴到和生成的 exe 文件同级的文件夹内

一般这两个文件都存在于 casadi 的安装目录下，即 casadi存放目录\install\casadi

配置环境变量

添加过链接库之后，还会提示找不到 casadi_nlpsol_ipopt.dll 文件的错误，就需要将 ipopt 的程序路径添加到系统环境变量中

ipopt存放目录\bin

一些其他的问题

vs2022 创建属性表闪退

在创建属性表时有时会遇到创建属性表之后 vs2022 卡死闪退的情况，解决方法如下

1. 在 Visual Studio Installer 中查看是否有 vs2022 的更新，如果有就更新到最新版
2. 使用 win+R 输入 cmd 打开终端，在其中输入指令 regsvr32 jscript9Legacy.dll 并运行

之后就可以成功创建了

casadi 求解 NMPC

利用简单的一阶倒立摆来验证算法

动力学分析

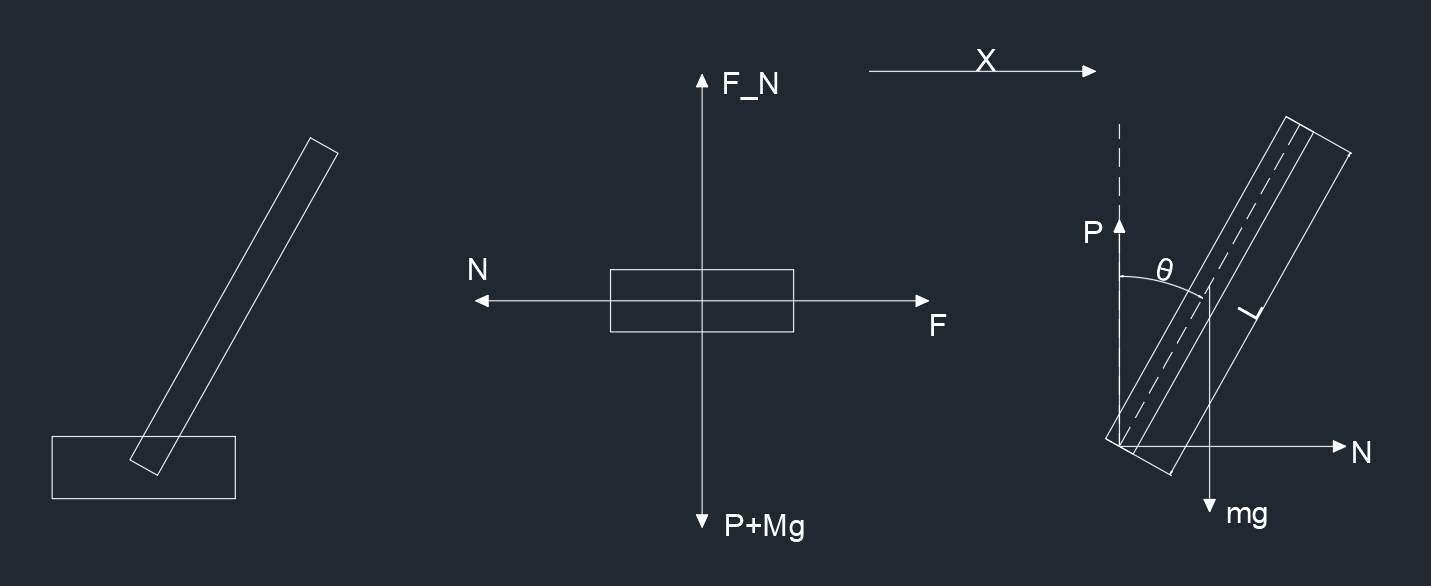
1. 底座分析

   1. x 方向上

      $M\ddot{x}=F-N\quad\text{\textcircled 1}$

   2. y 方向上

      $F_N=P+Mg$

2. 摆杆分析

   1. x 方向上

      $N=m(\ddot{x}+\frac{\partial^2}{\partial t^2}\frac{L\sin(\theta)}{2})\quad\text{\textcircled{2}}$

   2. y 方向上

      $P-mg=m\frac{\partial^2}{\partial t^2}\frac{L\cos(\theta)}{2}\quad\text{\textcircled{3}}$

   3. 扭矩

      $I_m\ddot{\theta}=\frac{PL\sin(\theta)}{2}-\frac{NL\cos(\theta)}{2}\quad\text{\textcircled{4}}$

求解系统状态空间方程

根据上述公式 $\text{\textcircled{1}}\sim\text{\textcircled{4}}$ 联立求解出 $\ddot{\theta},\ddot{x}$ ，如下

$\ddot{\theta}=\frac{Lm\Big[2g(m+M)\sin(\theta)-2F\cos(\theta)+L(m+2M)\dot{\theta}^2\sin(\theta)\cos(\theta)\Big]}{4I_m(m+M)+L^2m\big[M-(m+2M)\sin^2(\theta)\big]}\\\ddot{x}=-\frac{L m \dot{\theta}^2 \sin(\theta) (L^2m - 4I_m) - 2F (4I_m + L^2m \cos(2\theta)) + L^2g m^2 \sin(2\theta)}{2 \left( 4I_m (m + M) + L^2m \left[ M \cos^2(\theta) - (m + M) \sin^2(\theta) \right] \right)}$

设置 NMPC 的参数

计算完上述的 $\ddot{\theta},\ddot{x}$ 之后，还需要设定 NMPC 的步长，预测步数和权重矩阵

1. 步长的选择
   1. 对于快速动态系统，步长一般都较长，一般就是 10 ms 到 100 ms
   2. 对于高阶离散方法（例如 4 阶龙格库塔方法），允许使用较大点的步长
   3. 对于低阶方法（例如欧拉方法）需要更小的步长来保证精度
2. 预测步数选择
   1. 预测时域通常需要覆盖掉系统动态的过渡阶段，通常为系统稳定时间的 1-2 倍
   2. 步数过多会增加优化变量维度，可能超出实时计算能力，若需要减少计算量，可适当缩小预测步数或增大步长
3. 惩罚矩阵
   1. 状态跟踪误差权重矩阵 $Q$ ，用于调节状态误差的优先级
   2. 控制输入权重矩阵 $R$ ，用于限制控制输入的幅值或变化率
   3. 终端误差权重矩阵 $P$ ，用于强调终端状态的准确性
   4. 当 $Q$ 与 $R$ 过于接近的话，会导致 $U$ 的变化致使代价函数 $J$ 的变化不明显，从而最终求解得到的 $U$ 很小

可以设定一些初始值来计算代价函数，以此来设定 NMPC 的步长和预测步数，代码如下所示，可以根据设定一个初始的力 $F$ ，不断改变时间常数来计算相对应的代价函数，对比之后选择合适的时间常数。需要注意的是代价函数之间差别较小的话，会导致求解 NMPC 时陷入局部最优解，从而能很快得到结果，但是效果很差。若代价函数值过大的话，会导致计算周期长，甚至求解错误

predict_n = 10;
predict_step = 0.04;

x0 = [0; 0; 0; 0];
x_ref = [0; 0; 1; 0];
F_val = 0;
X = x0;
J = 0;
for i = 1 : 1 : predict_n
    theta_ddot_val = subs(theta_ddot, [theta(t), theta_dot, x(t), x_dot, F], [X(1, i), X(2, i), X(3, i), X(4, i), F_val]);
    x_ddot_val = subs(x_ddot, [theta(t), theta_dot, x(t), x_dot, F], [X(1, i), X(2, i), X(3, i), X(4, i), F_val]);
    X_dot = double([X(2, i); theta_ddot_val; X(4, i); x_ddot_val]);
    X = [X, X_dot * predict_step + X(:, i)];
end
J1 = 0;
Q = diag([10, 1, 10, 1]);
R = 1;
for i = 1 : 1 : predict_n + 1
    J1 = J1 + (X(:, i) - x_ref)' * Q * (X(:, i) - x_ref) + F_val' * R * F_val;
end
F_val = 10;
X = x0;
for i = 1 : 1 : predict_n
    theta_ddot_val = subs(theta_ddot, [theta(t), theta_dot, x(t), x_dot, F], [X(1, i), X(2, i), X(3, i), X(4, i), F_val]);
    x_ddot_val = subs(x_ddot, [theta(t), theta_dot, x(t), x_dot, F], [X(1, i), X(2, i), X(3, i), X(4, i), F_val]);
    X_dot = double([X(2, i); theta_ddot_val; X(4, i); x_ddot_val]);
    X = [X, X_dot * predict_step + X(:, i)];
end
J2 = 0;
Q = diag([10, 1, 10, 1]);
for i = 1 : 1 : predict_n + 1
    J2 = J2 + (X(:, i) - x_ref)' * Q * (X(:, i) - x_ref) + F_val' * R * F_val;
end
disp(J1);
disp(J2);

示例运行结果

该示例基于 webots+vs2022 平台实现。状态值为 $X=\begin{bmatrix}\theta\\\dot{\theta}\\x\\\dot{x}\end{bmatrix}$ ，设定目标值为 $X_{ref}=\begin{bmatrix}0\\0\\0.5\\0\end{bmatrix}$ ，运行结果如下

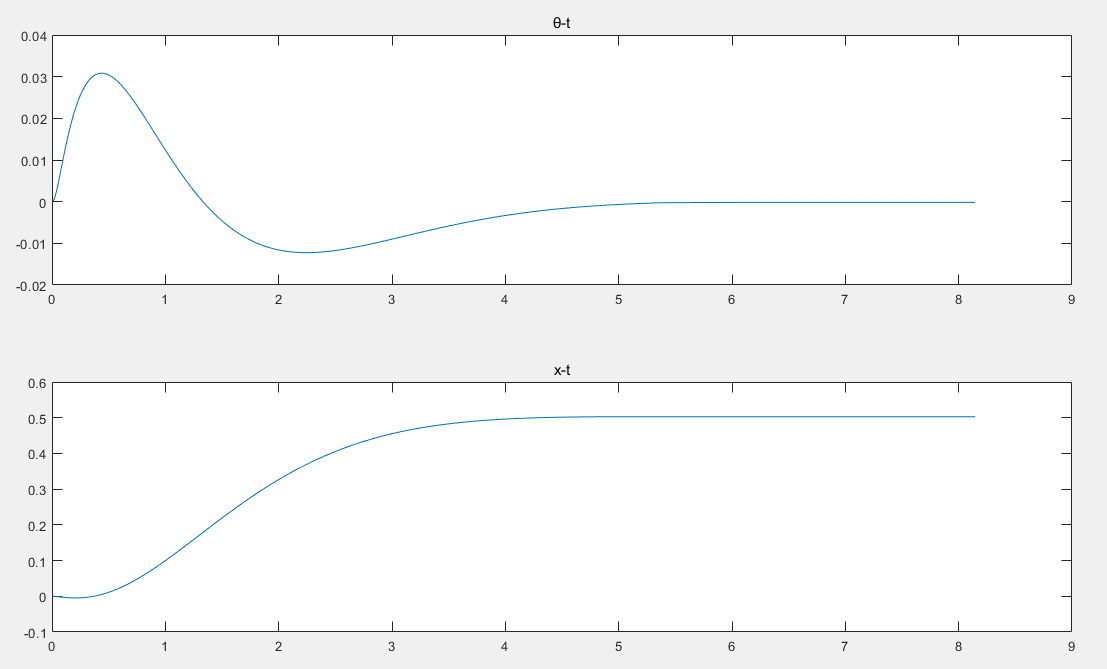
NMPC 求解器代码示例介绍

计算代价函数

SX  J = 0;
int i;
SX  U = SX::sym("u", control_n, predict_n);
SX  X = SX::sym("x", state_n, predict_n + 1);
SX  x0 = SX::sym("x0", state_n);
SX  x_ref = SX::sym("x_ref", state_n);
X(Slice(), 0) = x0;
for (i = 0; i < predict_n; ++i) {
  SX k1 = _dynamics(SXDict{ {"x", X(Slice(), i)}, {"u", U(Slice(), i)} }).at("xdot");
  SX k2 = _dynamics(SXDict{ {"x", X(Slice(), i) + 0.5 * predict_step * k1}, {"u", U(Slice(), i)} }).at("xdot");
  SX k3 = _dynamics(SXDict{ {"x", X(Slice(), i) + 0.5 * predict_step * k2}, {"u", U(Slice(), i)} }).at("xdot");
  SX k4 = _dynamics(SXDict{ {"x", X(Slice(), i) + 0.5 * predict_step * k3}, {"u", U(Slice(), i)} }).at("xdot");
  X(Slice(), i + 1) = X(Slice(), i) + (predict_step / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4);
}
for (i = 0; i < predict_n; ++i)
  J += SX::dot((X(Slice(), i) - x_ref), SX::mtimes(_Q, (X(Slice(), i) - x_ref))) + 
    SX::dot(U(Slice(), i), SX::mtimes(_R, U(Slice(), i)));
J += SX::mtimes((X(Slice(), i) - x_ref).T(), SX::mtimes(_Q, (X(Slice(), i) - x_ref)));

设定求解器的参数

SXDict nlp = {
  { "x", reshape(U, -1, 1) },
  { "f", J },
  { "p", vertcat(x0, x_ref) }
};

Dict opts;
opts["ipopt.max_iter"] = 5000;
opts["print_time"] = 0;
opts["ipopt.print_level"] = 0;
opts["ipopt.acceptable_tol"] = 1e-6;
opts["ipopt.acceptable_obj_change_tol"] = 1e-4;
solver = nlpsol("solver", "ipopt", nlp, opts);

求解结果

SX lbu = repmat(_u_min, predict_n, 1);
SX ubu = repmat(_u_max, predict_n, 1);
args["lbx"] = lbu;
args["ubx"] = ubu;
args["p"] = vertcat(x0, x_ref);
args["x0"] = DM::zeros(control_n * predict_n, 1);
DMDict res = solver(args);
return reshape(res.at("x"), control_n, predict_n);

代码地址

github 仓库

参考文章

1. CasADI嵌入式部署
2. VS2022新建props属性表闪退