概率分布

前言

概率分布（probability distribution）是给出事件发生的概率的函数，它是一种通过样本空间（sample space）和事件的概率描述随机事件的方式，下面有一些需要了解到的概念

---

边缘分布

假设有一个和两个变量相关的概率分布 $p(x,y)$ ，关于其中一个特定变量的边缘分布则为给定其他变量的条件概率分布如下

$p(x)=\sum_yp(x,y)=\sum_yp(x\vert y)p(y)$

---

偏度

偏度（Skewness）衡量数据分布的对称性，计算公式如下

$Skewness=\frac{E[(x-\mu)^3]}{\sigma^3}$

• $\mu$ 是均值
• $\sigma$ 是标准差
• $E$ 是期望值
• $Skewness=0$ 分布对称
• $Skewness>0$ 分布右偏，右侧尾部长
• $Skewness<0$ 分布左偏，左侧尾部长

---

峰度

峰度（Kurtosis）反映数据分布的尖锐程度和尾部厚度

$Kurtosis=\frac{E[(x-\mu)^4]}{\sigma^4}$

• $Kurtosis=3$ 正态分布的峰度
• $Kurtosis>3$ 分布更尖锐，尾部更厚
• $Kurtosis<3$ 分布更平坦，尾部更薄

---

离散均匀分布

离散均匀分布（Discrete Uniform Distribution） 是最简单的离散概率分布之一，描述了一个随机变量在有限个取值上具有相同概率的情况

---

离散均匀分布的概率质量函数

$f(X=x)=\frac{1}{n}\quad x=x_1,...x_n$

• $X$ 是随机变量，取值为 $x_1,…x_n$
• $n$ 是取值的个数
• 每个取值的概率相等，均为 $\frac{1}{n}$

对于取值是连续的整数，例如 $x=a,a+1,…b$ ，则概率质量函数可以表示为

$f(X=x)=\frac{1}{b-a+1}\quad x=a,a+1,…b$

---

性质

• 期望值为 $E[X]=\frac{1}{n}\sum_i^nx_i$
• 方差为 $Var(X)=\frac{1}{n}\sum_i^n(x_i-E[X])^2$
• 离散均匀分布是对称的，即所有取值的概率相等
• 离散均匀分布是连续均匀分布的离散版本
• 当多项分布的所有类别概率相等时，退化为离散均匀分布

---

连续均匀分布

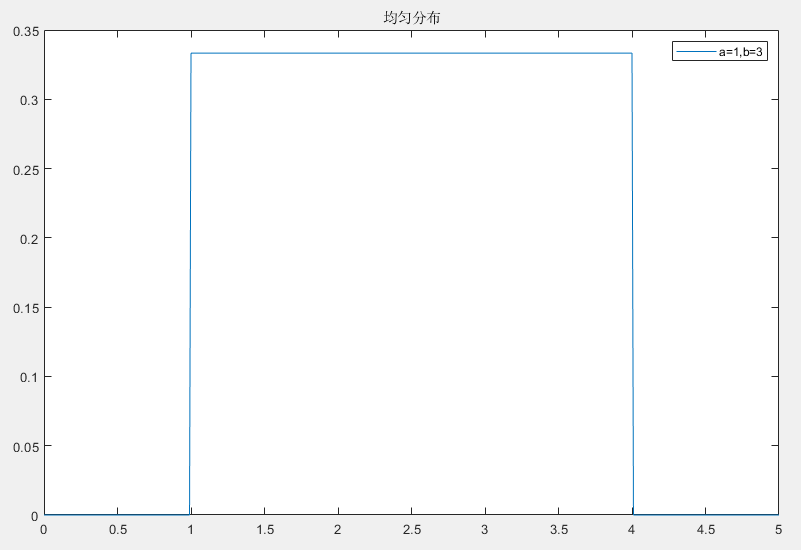
连续均匀分布（Continuous Uniforom Distribution）是概率论中最简单且常见的概率分布之一，它描述了一个随机变量在一定区间内取值的概率是均匀的

---

连续均匀分布的概率密度函数

连续均匀分布定义在一个区间 $[a,b]$ 中，随机变量在该区间内取值的概率密度是常数

$f(x)=\left\{\begin{aligned}&\frac{1}{b-a}&如果x\in[a,b]\\&0&其他\end{aligned}\right.$

• $a$ 是区间下限， $b$ 是区间上限， $b>a$

---

性质

• 期望值为 $E[X]=\frac{a+b}{2}$
• 方差 $Var(X)=\frac{(b-a)^2}{12}$
• 累积分布函数 $F(x)=\left\{\begin{aligned}&0&x<a\\&\frac{x-a}{b-a}&x\in[a,b]\\&1&x>b\end{aligned}\right.$
• 形状：概率密度在 $[a,b]$ 区间上是平坦的，区间外为 0

---

伯努利分布

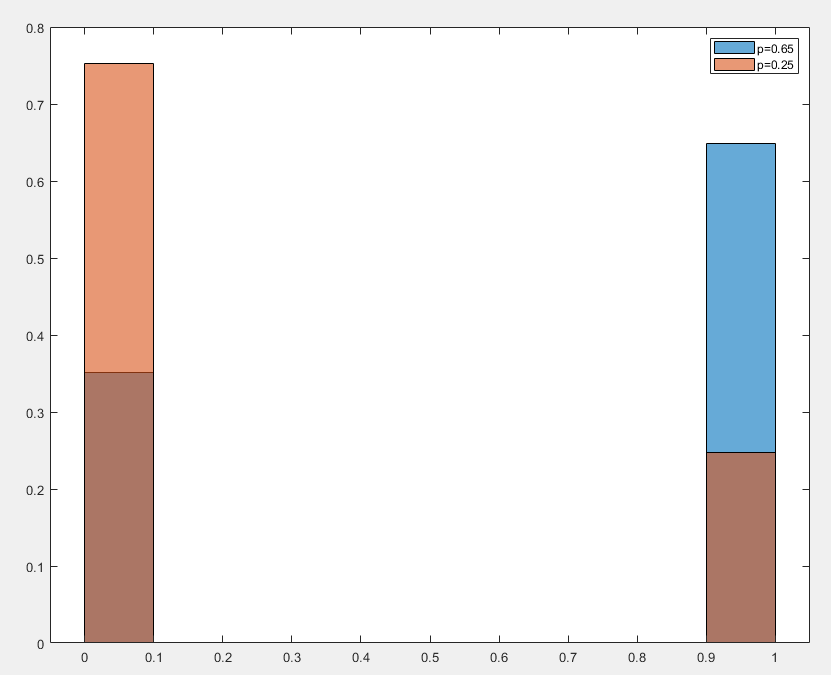
伯努利分布（Bernoulli Distribution） 是概率论中最简单的离散概率分布之一，用于描述只有两种可能结果的随机试验

---

定义

伯努利分布描述了一个随机试验，结果只有两种可能，其概率质量函数为

$p(x)=\left\{\begin{aligned}&p&&x=1\\&1-p&&x=0\end{aligned}\right.$

• $x$ 是随机变量，只能取 0 或 1
• $p$ 是成功的概率 $0\leq p\leq1$

---

性质

• 期望值为 $E[X]=p$
• 方差为 $Var(X)=p(1-p)$
• 偏度为 $Skewness=\frac{1-2p}{\sqrt{p(1-p)}}$
• 峰度为 $Kurtosis=\frac{1-3p(1-p)}{p(1-p)}$

---

高斯分布

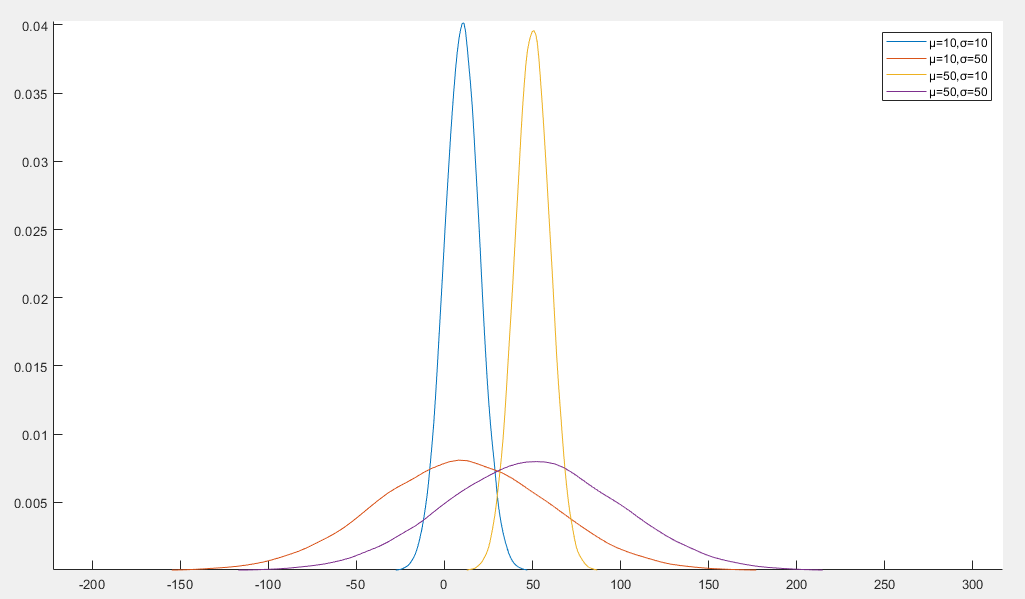
高斯分布（Gaussian Distribution）又称为正态分布（Normal Distribution）

---

概率密度函数

$f(x)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp(-\frac{(x-\mu)^2}{2\sigma^2})$

• $\mu$ 是均值，决定分布的中心值
• $\sigma^2$ 是方差

---

性质

• 对称性：关于均值对称
• 钟形曲线：呈单峰钟形，峰值在 $x=\mu$ 处
• 标准正态分布的累积分布函数为 $\Phi(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^xe^{-t^2/2}dt$
• 高斯分布的累积分布函数为 $F(x)=\Phi(\frac{x-\mu}{\sigma})$
• 有 68% 在 $\mu\plusmn\sigma$ 内
• 有 95% 在 $\mu\plusmn2\sigma$ 内
• 有 99.7% 在 $\mu\plusmn3\sigma$ 内
• 线性变换：若 $x\sim\mathcal{N}(\mu,\sigma^2)$ 则 $aX+b\sim\mathcal{N}(a\mu+b,a^2\sigma^2)$

---

标准正态分布

当 $\mu=0$ 且 $\sigma=1$ 时称为标准正态分布，概率密度函数为

$f(x)=\frac{1}{\sqrt{2\pi}}\exp(-\frac{x^2}{2})$

---

混合高斯分布

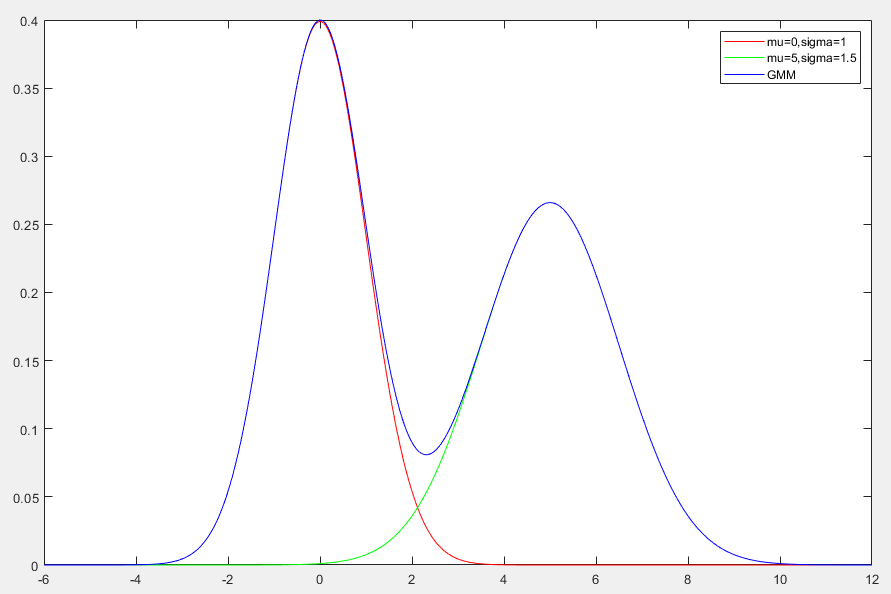
混合高斯分布（Gaussian Mixture Model, GMM）是由多个高斯分布线性组合而成的概率分布，常用于对复杂数据分布的建模

---

概率密度函数

$p(x)=\sum_k^K\pi_k\mathcal{N}(x\vert\mu_k,\Sigma_k)$

• $K$ 是高斯分布的数量
• $\pi_k$ 是第 $k$ 个高斯分布的混合系数（权重），满足 $\sum_k^K\pi_k=1,\pi_k\geq0$
• $\mathcal{N}(x\vert\mu_k,\Sigma_k)$ 是第 $k$ 个高斯分布的概率密度函数， $\mu_k$ 是均值， $\Sigma_k$ 是协方差

---

性质

• 期望值为 $E[X]=\sum_k^K\pi_k\mu_k$
• 协方差矩阵为 $Cov(X)=\sum_k^K\pi_k(\Sigma_k+(\mu_k-E[X])(\mu_k-E[X])^T)$
• 灵活性：通过调整高斯分布的数量 $K$ 和参数，可以模拟各种复杂分布
• 多峰性：混合高斯分布可以描述多峰数据，而单一高斯分布只能描述单峰数据

---

多元高斯分布

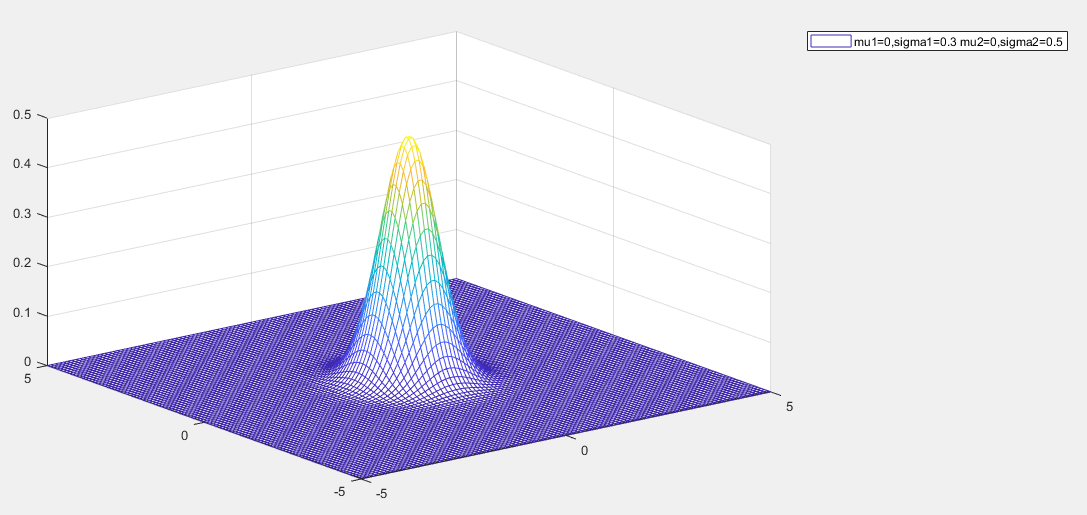
多元高斯分布（Multivariate Gaussian Distribution）是单变量高斯分布在多维空间中的推广，用于描述多个随机变量的联合分布

---

概率密度函数

$p(x)=\frac{1}{(2\pi)^{n/2}\vert\Sigma\vert^{1/2}}\exp(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu))$

• $x$ 是 n 维随机向量
• $\mu$ 是均值向量，表示各变量的期望值
• $\Sigma$ 是协方差矩阵
• $\vert\Sigma\vert$ 是协方差矩阵的行列式

---

性质

• 均值向量 $\mu$ 决定分布的中心位置
• 协方差矩阵 $\Sigma$ 控制分布的形态和方向
• 若协方差矩阵为对角矩阵，变量间相互独立
• 对多元高斯随机向量进行线性变换，结果仍为多元高斯分布

---

瓦尔德分布

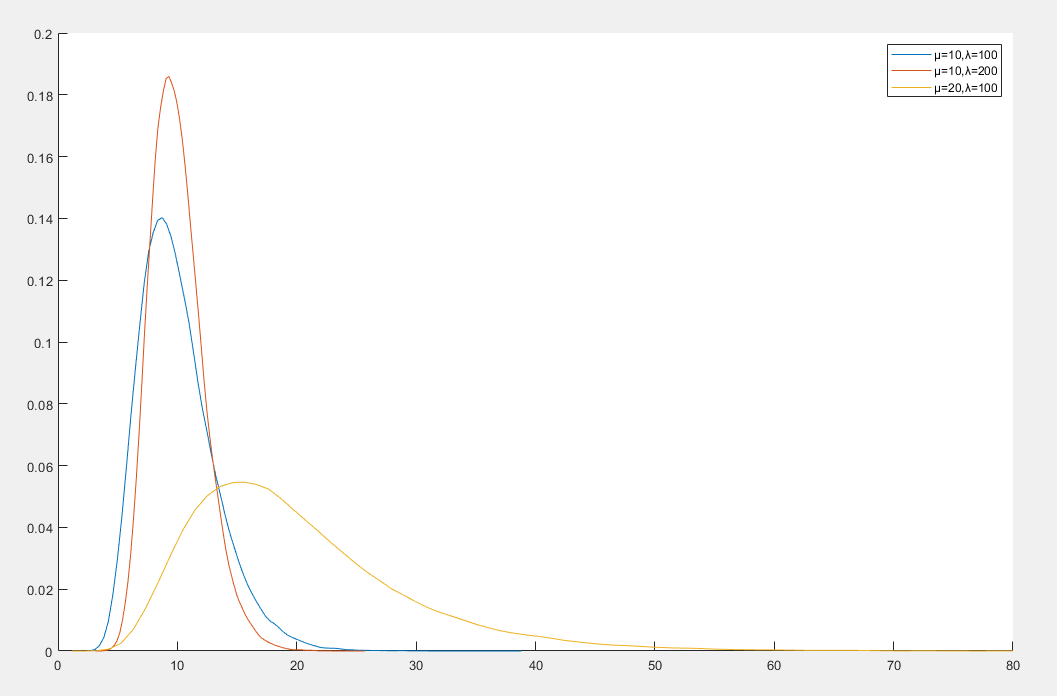
瓦尔德分布（Wald Distribution）也称为逆高斯分布（Inverse Gaussian Distribution），是一种连续概率分布，常用于描述正偏态数据

---

瓦尔德分布的概率密度函数

$f(x)=\sqrt{\frac{\lambda}{2\pi x^3}}\exp(-\frac{\lambda(x-\mu)^2}{2\mu^2x})\quad x>0$

• $x$ 是随机变量
• $\mu$ 是均值
• $\lambda$ 是形状参数

---

性质

• 期望值为 $E[X]=\mu$
• 方差为 $Var(X)=\frac{\mu^3}{\lambda}$
• 瓦尔德分布描述了布朗运动首次达到某一固定水平的时间分布
• 可加性：对于两个独立的瓦尔德分布随机变量 $X_1\sim Wald(\mu_1,\lambda_1)$ 和 $X_2\sim Wald(\mu_2,\lambda_2)$ ，则它们的和也服从瓦尔德分布 $X_1+X_2\sim Wald(\mu_1+\mu_2,(\lambda_1^{-1}+\lambda_2^{-1})^{-1})$
• 当 $\lambda\rightarrow\infty$ 时，瓦尔德分布趋近于正态分布
• 瓦尔德分布与伽马分布有相似的性质，但瓦尔德分布更适合描述正偏态数据

---

卡方分布

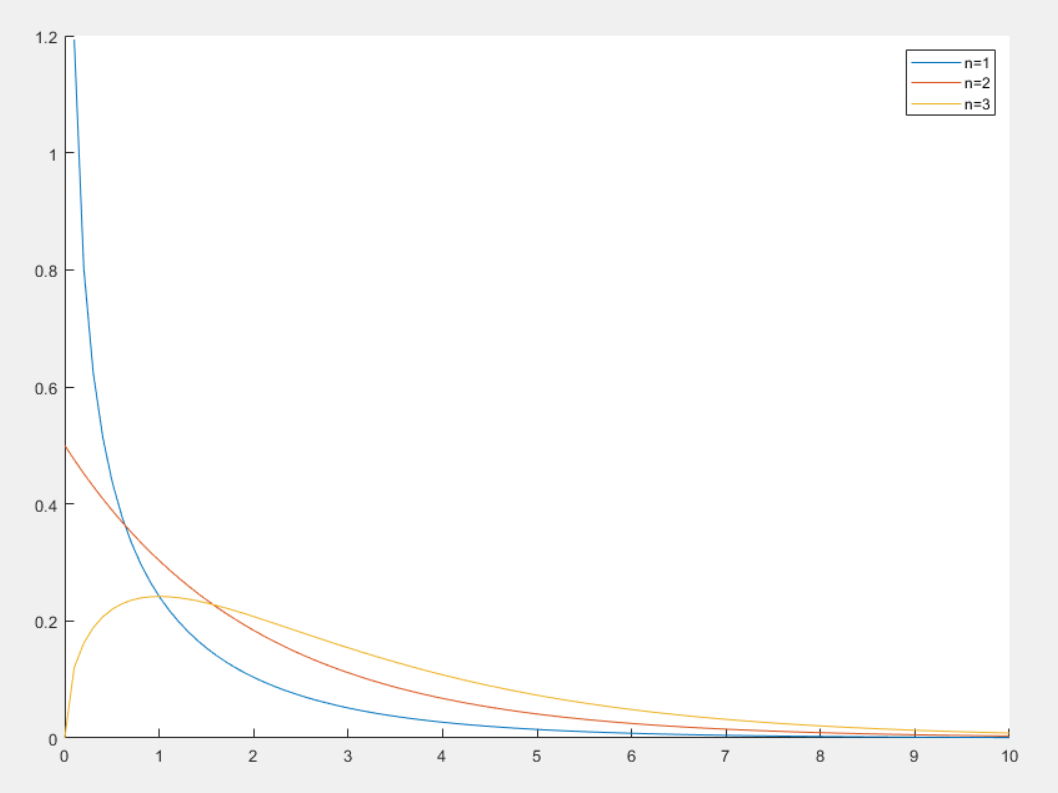
卡方分布（Chi-Square Distribution）是概率论与统计学中常用的一种连续概率分布，常用于假设检验和置信区间的计算

---

定义

设 $x_1,…x_n\sim N(0,1)$ ，令 $X=\sum_i^nx_i^2$ ，则称 $X$ 是自由度为 $n$ 的 $\chi^2$ 分布，记作 $X\sim\chi^2$

对于随机变量 $X\sim\chi^2$ ，其概率密度函数如下

$f(x)=\left\{\begin{aligned}&\frac{x^{\frac{n}{2}-1}e^{-\frac{x}{2}}}{2^{\frac{n}{2}}\Gamma(\frac{n}{2})}&x>0\\&0&x\leq 0\end{aligned}\right.$

其中 $\Gamma(x)=\int_0^\infty t^{x-1}e^{-t}dt\quad (x>0)$

---

性质

• 卡方分布的定义域为 $x>0$ ，卡方随机变量总是非负的
• 期望值为 $E[X]=n$
• 方差为 $Var(X)=2n$
• 当自由度 $n$ 较小时，卡方分布右偏，随着 $n$ 增大，分布逐渐对称并接近正态分布
• 对于随机变量 $X\sim \chi_n^2$ 有 $E(X)=n,Var(X)=2n$
• 对于两个随机变量 $Z_1\sim\chi_{n_1}^2$ 和 $Z_2\sim\chi_{n_2}^2$ ，并且两个随机变量相互独立，则 $Z_1+Z_2\sim\chi_{n_1+n_2}^2$
• 当 $n\rightarrow\infty$ 时，卡方分布趋近于正态分布 $N(n,2n)$

---

t 分布

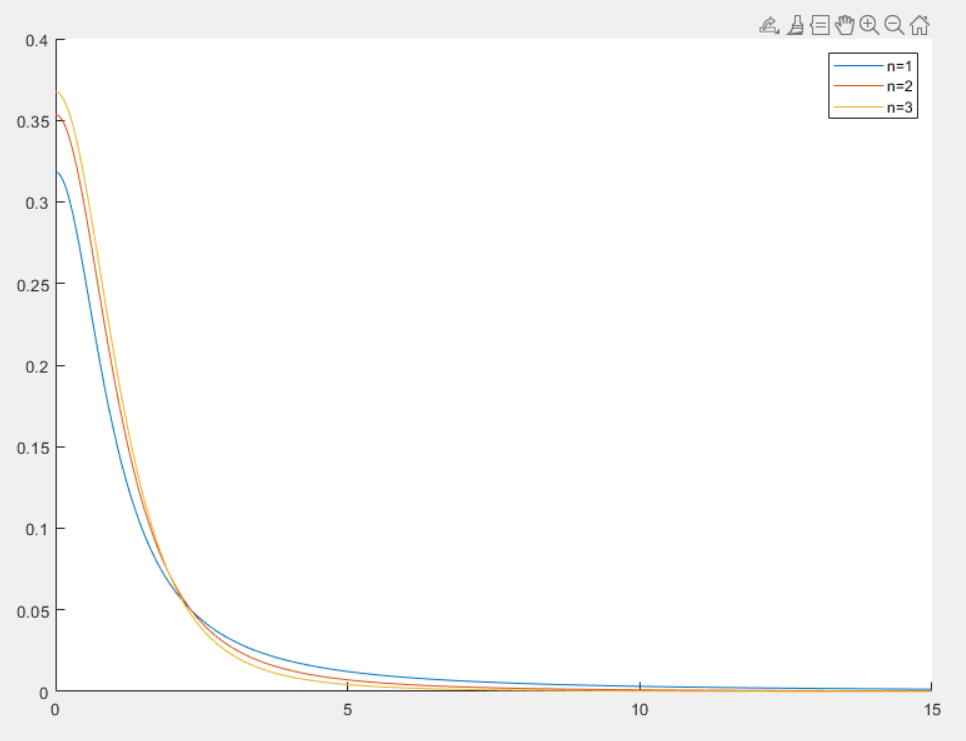
t 分布（Student’s t-distribution）是统计学中常用的一种连续概率分布，主要用于小样本情况下的假设检验和置信区间估计

---

定义

设随机变量 $X\sim N(0,1)$ 和 $Y\sim\chi_n^2$ ，且 $X$ 和 $Y$ 独立，则称

$T=\frac{X}{\sqrt{\frac{Y}{n}}}$

为自由度 $n$ 的 $t$ 变量，其分布称为自由为 $n$ 的 t 分布，记作 $T\sim t_n$

对于随机变量 $T\sim t_n$ ，其密度函数如下

$f(x)=\frac{\Gamma(\frac{n+1}{2})}{\Gamma(\frac{n}{2})\sqrt{n\pi}}(1+\frac{x^2}{n})^{-\frac{n+1}{2}}\quad x\in(-\infty,+\infty)$

---

性质

• 期望值为 $E[T]=0\quad n>1$
• 方差为 $Var(T)=\frac{n}{n-2}\quad n>2$ ，否则方差不存在
• 对于随机变量 $T\sim t_n$ ，则当 $n\geq2$ 时，均值 $E(T)=0$ 。当 $n\geq3$ 时，方差 $Var(T)=\frac{n}{n-2}$
• 当 $n\rightarrow\infty$ 时，t 变量的极线分布为 $N(0,1)$

---

F 分布

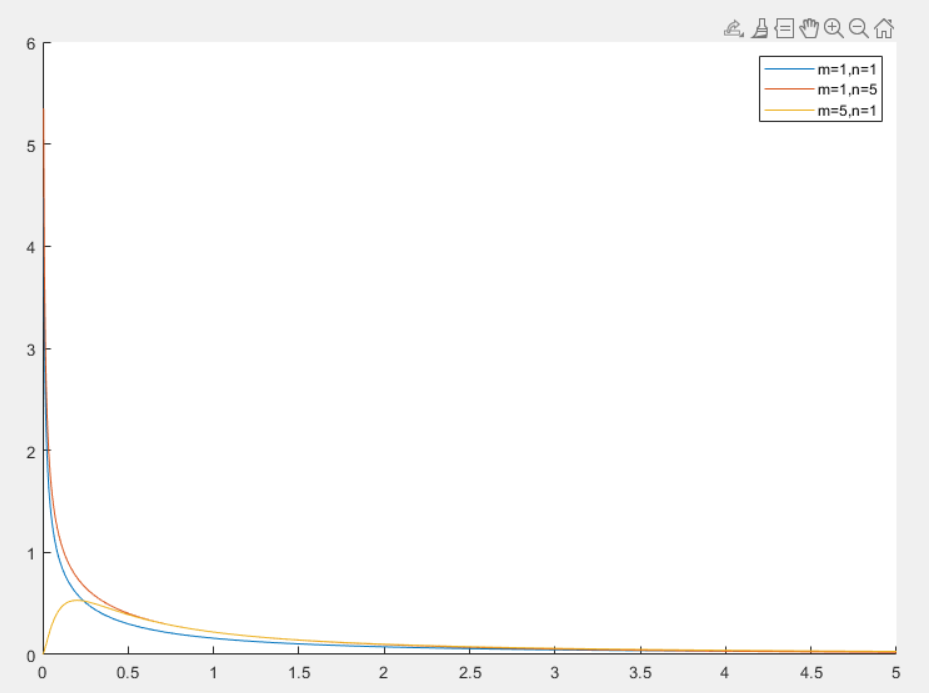
F 分布（F-distribution）是统计学中常用的一种连续概率分布，主要用于比较两个样本方差的分布情况

---

定义

对于两个随机变量 $X\sim\chi_m^2$ 和 $Y\sim\chi_n^2$ ，并且两个变量相互独立，则称

$F=\frac{X/m}{Y/n}$

为自由度分别是 $m$ 和 $n$ 的 F 变量，其分布称为自由度分别是 $m$ 和 $n$ 的 F 分布，记作 $F\sim F_{m,n}$

对于随机变量 $X\sim F_{m,n}$ 其概率密度函数如下

$f_{m,n}(x)=\left\{\begin{aligned}&\frac{\Gamma(\frac{m+n}{2})}{\Gamma(\frac{n}{2})\Gamma(\frac{m}{2})}m^{\frac{m}{2}}n^{\frac{n}{2}}x^{\frac{m}{2}-1}(n+mx)^{-\frac{m+n}{2}}&x>0\\&0&x\leq0\end{aligned}\right.$

---

性质

• 期望值为 $E[F]=\frac{n}{n-2}\quad n>2$
• 方差为 $Var(F)=\frac{2n^2(m+n-2)}{m(n-2)^2(n-4)}\quad n>4$
• 若 $X\sim F_{m,n}$ 则 $\frac{1}{X}\sim F_{n,m}$
• 若 $X\sim t_n$ 则 $X^2\sim F_{1,n}$
• $F_{m,n}(1-\alpha)=\frac{1}{F_{n,m}(\alpha)}$
• 当 $m$ 和 $n$ 较小时，分布偏右，随着逐渐增大，分布逐渐对称

---

二项分布

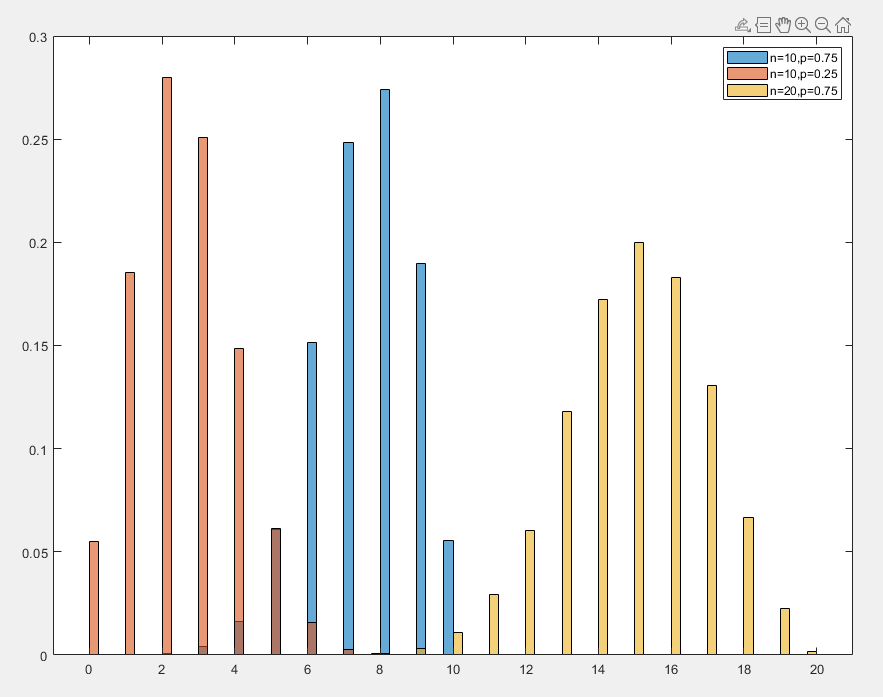
二项分布（Binomial Distribution）是一种离散概率分布，用于描述在 $n$ 次独立实验中，某事件正好发生 $k$ 次的概率。对于一个随机变量 $X$ ，如果其满足二项分布，则称其 $X\sim Binomial(n,p)$

---

概率质量函数

$P(X=k)=\left(\begin{matrix}n\\k\end{matrix}\right)p^k(1-p)^{n-k}\quad k=0,1,....n$

• $X$ 是随机变量，表示事件发生的次数
• $k$ 是事件发生的具体次数
• $n$ 是试验的总次数
• $p$ 是每次实验中事件发生的概率
• $\left(\begin{matrix}n\\k\end{matrix}\right)$ 是组合数，表示从 $n$ 次试验中选出 $k$ 次成功的方式数 $\left(\begin{matrix}n\\k\end{matrix}\right)=\frac{n!}{k!(n-k)!}$

---

性质

• 期望值为 $E[X]=np$
• 方差为 $Var(X)=np(1-p)$
• 矩生成函数 $M_X(t)=(1-p+pe^t)^n$
• 特征函数为 $\Phi_X(t)=(1-p+pe^{it})^n$ 其中 $i$ 是虚数单位
• 可加性：对于两个独立的二项随机变量 $X_1\sim Binomial(n_1,p)$ 和 $X_2\sim Binomial(n_2,p)$ ，则它们的和也满足二项分布 $X_1+X_2\sim Binomial(n_1+n_2,p)$

---

负二项分布

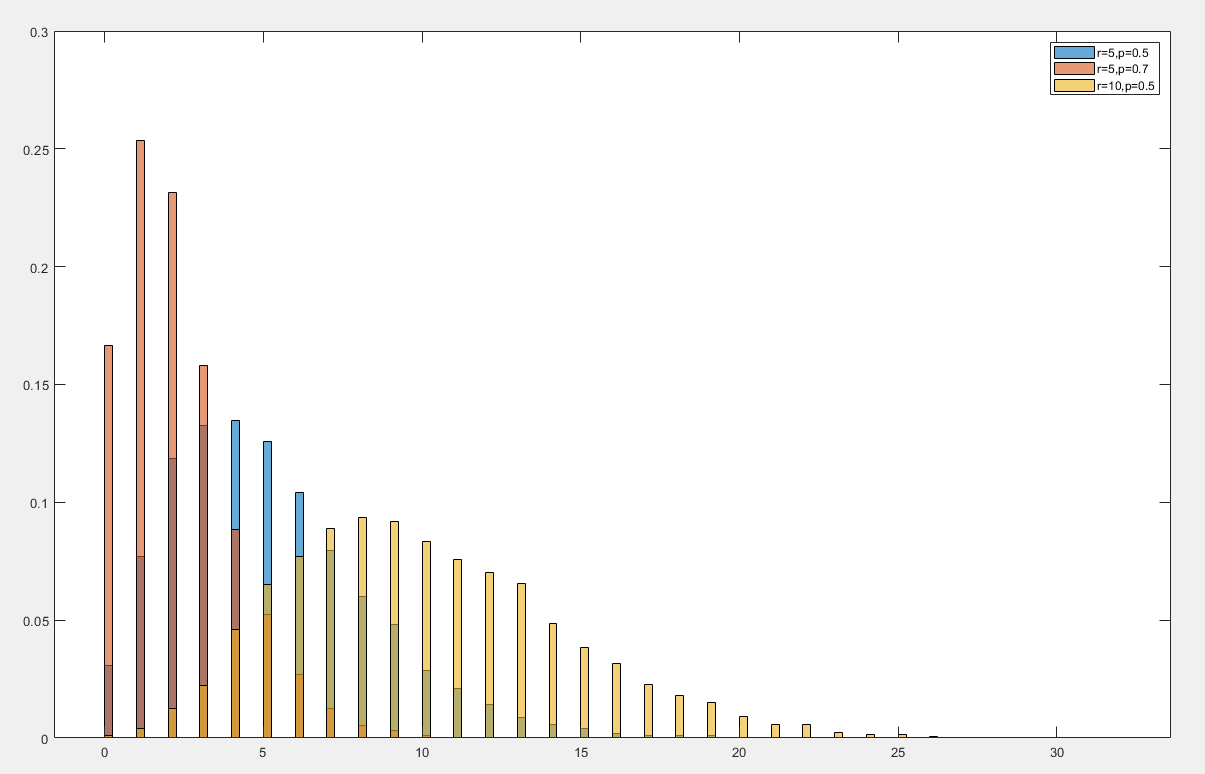
负二项分布（Negative Binomial Distribution）是一种离散概率分布，用于描述在一系列独立伯努利试验中，达到指定次数的成功所需的试验次数

---

负二项分布的概率质量函数

• 根据试验次数定义：随机变量 $X$ 表示达到 $r$ 次成功所需要的总实验次数，包括成功的

  $P(X=k)=\left(\begin{matrix}k-1\\r-1\end{matrix}\right)p^r(1-p)^{k-r}\quad k=0,1...$

• 根据失败次数定义：随机变量 $Y$ 表示达到 $r$ 次成功前的失败次数

  $P(Y=k)=\left(\begin{matrix}k+r-1\\r-1\end{matrix}\right)p^r(1-p)^{k-r}\quad k=0,1...$

其中

• $k$ 是试验次数或者失败次数
• $r\geq1$ 是成功次数
• $p$ 是每次试验的成功概率
• $1-p$ 是每次试验中失败的概率
• $\left(\begin{matrix}n\\k\end{matrix}\right)$ 是组合数，表示从 $n$ 次试验中选出 $k$ 次成功的方式数 $\left(\begin{matrix}n\\k\end{matrix}\right)=\frac{n!}{k!(n-k)!}$

---

性质

• 期望值为 $E[X]=\frac{r}{p}\quad E[Y]=\frac{r(1-p)}{p}$
• 方差为 $Var(X)=\frac{r(1-p)}{p^2}\quad Var(Y)=\frac{r(1-p)}{p^2}$
• 矩生成函数为 $M_X(t)=(\frac{pe^t}{1-(1-p)e^t})^r\quad M_Y(t)=(\frac{pe^t}{1-(1-p)e^t})^r\quad t<-\ln(1-p)$
• 可加性：对于两个独立的负二项随机变量 $X_1\sim NegativeBinomial(r_1,p)$ 和 $X_2\sim NegativeBinomial(r_2,p)$ ，则它们的和也满足二项分布 $X_1+X_2\sim NegativeBinomial(r_1+r_2,p)$
• 当 $r=1$ 时退化为几何分布，几何分布描述第一次成功所需的试验次数，而负二项分布描述第 $r$ 次成功所需的试验次数
• 当 $r\rightarrow\infty,p\rightarrow1$ 时，负二项分布可近似为泊松分布
• 二项分布描述固定试验次数中的成功次数，而负二项分布描述固定成功次数所需的试验次数

---

泊松分布

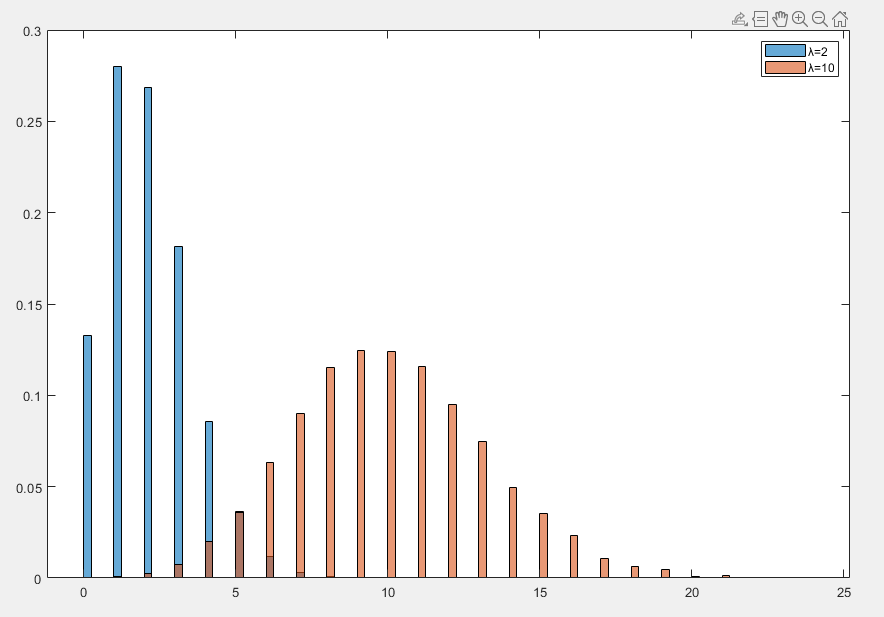
泊松分布（Poisson Distribution）是一种离散概率分布，用于描述在固定时间或空间内某事件发生的次数的概率分布。对于一个随机变量 $X$ ，如果其满足泊松分布，则称其 $X\sim Poisson(\lambda)$

---

概率质量函数

泊松分布的概率质量函数为

$P(X=k)=\frac{\lambda^ke^{-\lambda}}{k!}\quad k=0,1,....n$

• $X$ 是随机变量，表示事件发生的次数
• $k$ 是事件发生的具体次数
• $\lambda$ 是分布的参数，示在固定时间或空间内事件发生的平均次数
• $e$ 是自然对数的底

---

性质

• 期望值为 $E[X]=\lambda$

• 方差为 $Var(X)=\lambda$

• 矩生成函数为 $M_X(t)=\exp(\lambda(e^t-1))$

• 特征函数 $\Phi_X(t)=\exp(\lambda(e^{it}-1))$ ，其中 $i$ 是虚数单位

• 可加性：对于两个独立的泊松随机变量 $X_1\sim Poisson(\lambda_1)$ 和 $X_2\sim Poisson(\lambda_2)$ ，则它们的和也满足泊松分布 $X_1+X_2\sim Poisson(\lambda_1+\lambda_2)$

• 泊松分布可以看作是二项分布的极限情况，当二项分布的试验次数 $n$ 很大时，并且单次成功概率很小，并且 $\lambda=np$ 保持常数时，二项分布近似于泊松分布

  $Binomial(n,p)\approx Poisson(\lambda=np)\quad n\rightarrow\infty,p\rightarrow0$

---

几何分布

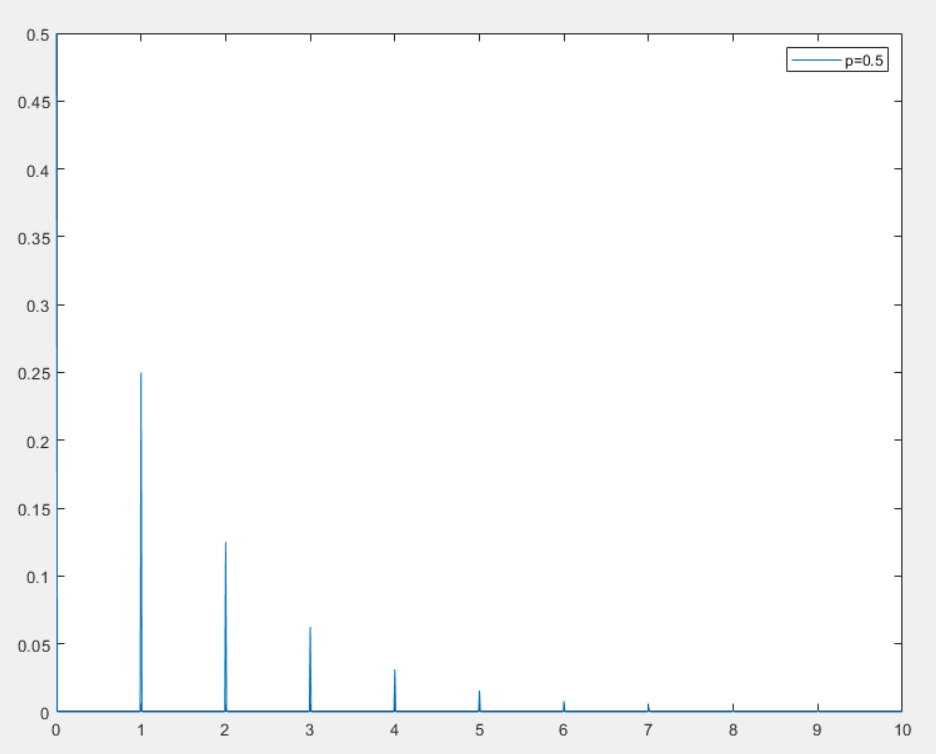
几何分布（Geometric Distribution）是一种离散概率分布，用于描述在一系列独立伯努利试验中，第一次成功所需的试验次数

---

几何分布的概率质量函数

• 对于第一次成功所需要的试验次数

  $P(X=k)=(1-p)^{k-1}p\quad k=1,2,....$

• 对于第一次成功前的失败次数

  $P(Y=k)=(1-p)^{k}p\quad k=1,2,....$

其中

• $k$ 是失败的次数或者试验次数
• $p$ 是每次试验中成功的概率

---

性质

• 期望值为 $E[X]=\frac{1}{p}\quad E[Y]=\frac{1-p}{p}$

• 方差为 $Var(X)=\frac{1-p}{p^2}\quad Var(Y)=\frac{1-p}{p^2}$

• 矩生成函数为 $M_X(t)=\frac{pe^t}{1-(1-p)e^t}\quad M_Y(t)=\frac{pe^t}{1-(1-p)e^t}\quad t<-\ln(1-p)$

• 无记忆性：几何分布是唯一具有无记忆性的离散分布，过去的失败对未来成功的概率没有影响

  $P(X>k+n\vert X>k)=P(x>n)\quad k,n>0$

• 几何分布是负二项分布的特例，当负二项分布的成功次数 $r=1$ 时，负二项分布退化为几何分布

---

超几何分布

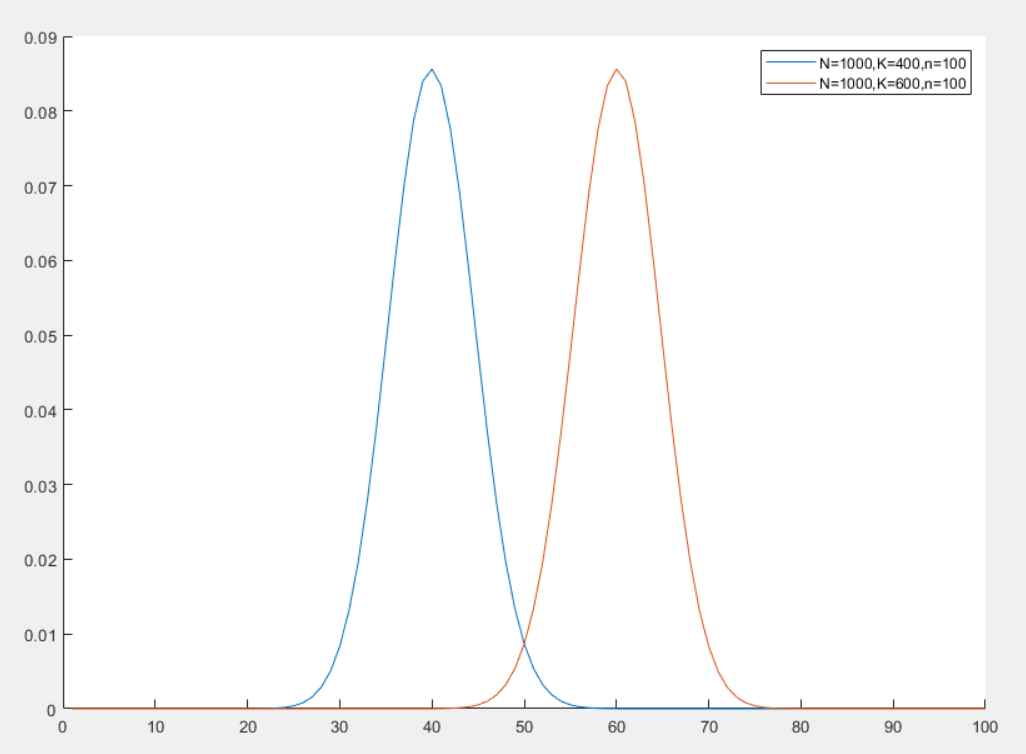
超几何分布（Hypergeometric Distribution）是一种离散分布，用于描述在不放回抽样中成功次数的分布

---

超几何分布的概率质量函数

超几何分布描述的是从有限的 $N$ 个物品中不放回的抽取 $n$ 个物品，其中包含 $K$ 个成功物品和 $N-K$ 个失败物品，成功物品的个数服从超几何分布，其概率质量函数为

$P(X=k)=\frac{\left(\begin{matrix}K\\k\end{matrix}\right)\left(\begin{matrix}N-K\\n-k\end{matrix}\right)}{\left(\begin{matrix}N\\n\end{matrix}\right)}$

• $\left(\begin{matrix}n\\k\end{matrix}\right)$ 是组合数，表示从 $n$ 次试验中选出 $k$ 次成功的方式数 $\left(\begin{matrix}n\\k\end{matrix}\right)=\frac{n!}{k!(n-k)!}$

---

性质

• 期望值为 $E[X]=n\frac{K}{N}$
• 方差为 $Var(X)=n\frac{K}{N}(1-\frac{K}{N})\frac{N-n}{N-1}$
• 当 $N$ 很大而 $n$ 相对较小时，超几何分布近似于二项分布 $B(n,p)$ ，其中 $p=\frac{K}{N}$

---

指数分布

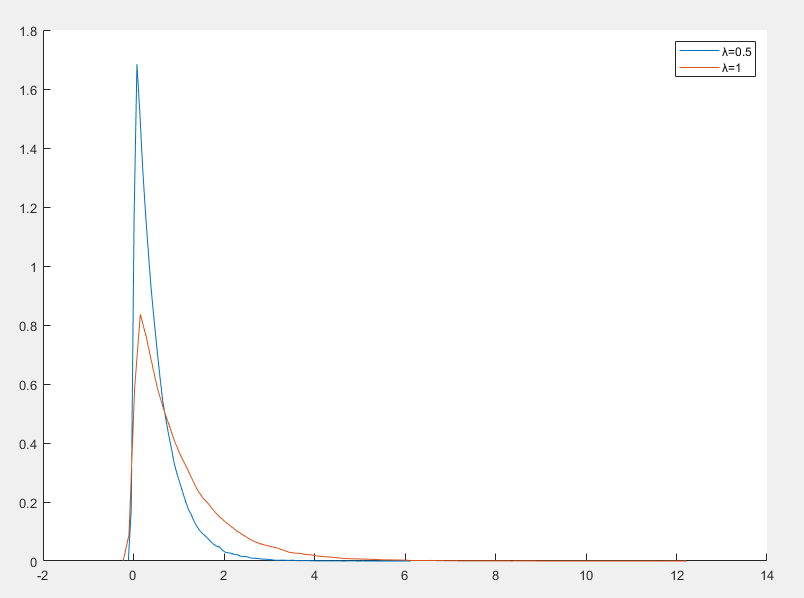
指数分布（Exponential Distribution）是一种连续概率分布，通常用于描述事件之间的时间间隔或等待时间，是唯一具有无记忆性（Memoryless Property）的连续分布

---

指数分布的概率密度函数

$f(x\vert\lambda)=\lambda e^{-\lambda x}\quad x\geq0$

• $x$ 是随机变量，表示事件之间的事件间隔或等待时间
• $\lambda>0$ 是速率参数，表示单位时间内事件发生的平均次数

也可以用尺度参数 $\theta=\frac{1}{\lambda}$ 来表示

$f(x\vert\theta)=\frac{1}{\theta}e^{-x/\theta}$

• $\theta$ 是尺度参数，表示事件之间的平均时间间隔

---

性质

• 期望值为 $E[X]=\frac{1}{\lambda}=\theta$

• 方差为 $Var(X)=\frac{1}{\lambda^2}=\theta^2$

• 矩生成函数为 $M_X(t)=\frac{\lambda}{\lambda-t}\quad t<\lambda$

• 特征函数为 $M_X(t)=\frac{\lambda}{\lambda-it}$

• 无记忆性：过去的事件对未来事件的概率没有影响

  $P(X>s+t\vert X>s)=P(X>t)\quad s,t>0$

• 如果事件在单位时间内发生的次数服从泊松分布 $Poisson(\lambda)$ ，则事件之间的时间间隔服从指数分布 $EXP(\lambda)$

• 指数分布是伽马分布的特例，当伽马分布的形状参数 $k=1$ 时伽马分布退化为指数分布

• 指数分布是几何分布的连续版本

---

伽马分布

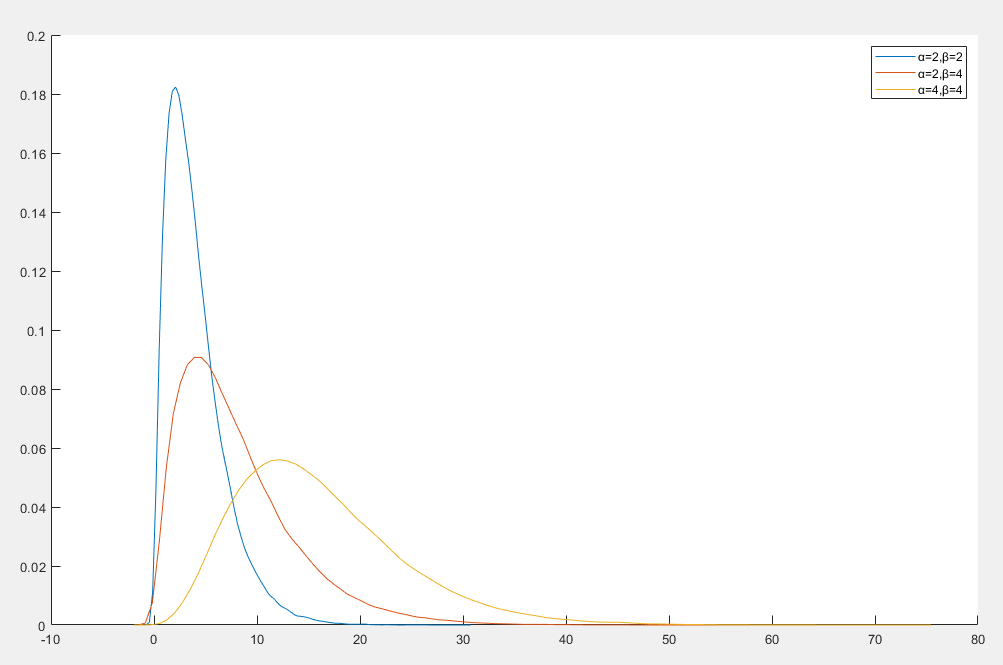
伽马分布是一种连续概率分布，用于建模正实数值的随机变量，如果一个随机变量服从于伽马分布，记作 $X\sim\Gamma_p(\alpha,\beta)$

---

概率密度函数

$f(x\vert\alpha,\beta)=\frac{\beta^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\beta x}\quad x>0$

• $x>0$ 是随机变量
• $\alpha>0$ 是形状参数
• $\beta>0$ 是尺度参数
• $\Gamma(\alpha)=\int_0^\infty x^{\alpha-1}e^{-x}dx$ 是伽马参数

---

性质

• 期望值为 $E[X]=\frac{\alpha}{\beta}$
• 方差值为 $Var(X)=\frac{\alpha}{\beta^2}$
• 当 $\alpha=1$ 时，伽马分布退化为指数分布
• 当 $\alpha=\frac{n}{2}$ 并且 $\beta=\frac{1}{2}$ 时，伽马分布就是自由度为 $n$ 的卡方分布
• 可加性，对于两个独立的随机变量 $X\sim \Gamma_p(a,\beta)$ 和 $Y\sim \Gamma_p(b,\beta)$ ，则 $Z=X+Y\sim \Gamma_p(a+b,\beta)$
• 特征函数 $\Phi_X(t)=(1-i\cdot\theta t)^{-k}$ ，其中 $i$ 是虚数单位
• 矩生成函数 $M_X(t)=(1-\theta t)^{-k}\quad t<\frac{1}{\theta}$

---

逆伽马分布

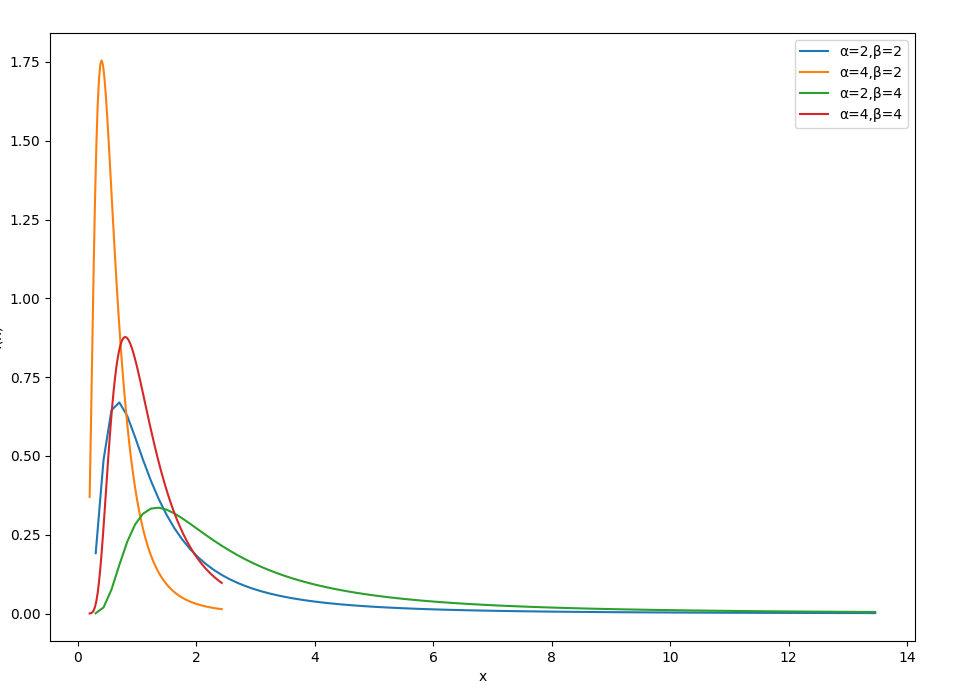
逆伽马分布（Inverse gamma distribution）是伽马分布的逆分布，通常用于建模正实数值的随机变量，如果一个随机变量服从于逆伽马分布，记作 $X\sim\Gamma_p^{-1}(\alpha,\beta)$

---

概率密度函数

$f(x\vert\alpha,\beta)=\frac{\beta^\alpha}{\Gamma(\alpha)}x^{-\alpha-1}e^{-\beta x}\quad x>0$

• $\alpha>0$ 是形状参数
• $\beta>0$ 是尺度参数

---

性质

• 如果 $X\sim\Gamma_p(\alpha,\beta)$ ，则 $Y=\frac{1}{X}\sim\Gamma_p^{-1}(\alpha,\beta)$
• 期望值为 $E[X]=\frac{\beta}{\alpha-1}\quad\alpha>1$
• 方差为 $Var(X)=\frac{\beta^2}{(\alpha-1)^2(\alpha-2)}\quad\alpha>2$

---

威沙特分布

威沙特分布（Wishart Distribution）是多元高斯分布的协方差矩阵的分布，通常用于建模正定对称矩阵

---

威沙特分布的概率密度函数

$f(X)=\frac{\vert X\vert^{\frac{n-p-1}{2}}\exp(-\frac{1}{2}tr(\Sigma^{-1}X))}{2^{\frac{np}{2}}\vert\Sigma\vert^\frac{n}{2}\Gamma_p(\frac{n}{2})}$

对于 $X\in R^{n\times p}$ 的随机矩阵，其列向量独立同分布于 $N_p(M,\Sigma)$ ，则 $W=X^TX$ 服从自由度为 $n$ ，非中心参数矩阵 $\Omega=M^T\Sigma^{-1}M$ 的非中心威沙特分布，记作 $W\sim W_p(n,\Sigma,\Omega)$

• $p$ 维度
• $n\geq p$ 自由度
• $\Sigma\in R^{p\times p}$ 协方差矩阵
• $\Omega\in R^{p\times p}$ 的非中心参数矩阵
• $tr$ 表示矩阵的迹

特别的，当 $M=0$ 时 $W=X^TX$ 服从于自由度为 $n$ 的中心威沙特分布，记作 $W\sim W_p(n,\Sigma)$

---

性质

• 非中心威沙特分布的期望值为 $E[W]=n\Sigma+M^TM$
• 中心威沙特分布的期望值为 $E[W]=n\Sigma$
• 协方差为 $Cov(W_{ij},W{kl})=n(\Sigma_{ik}\Sigma_{jl}+\Sigma_{il}\Sigma_{jk})$
• 非中心威沙特分布特征函数为 $\Phi_W(T)=\vert I_p-2i\Sigma T\vert^{-n/2}\exp(i\cdot tr(T(I_p-2i\Sigma T)^{-1}\Omega))$ 其中 $i$ 是虚数单位
• 非中心威沙特分布特征函数为 $\Phi_W(T)=\vert I_p-2i\Sigma T\vert^{-n/2}$
• 可加性：若 $W_1\sim W_p(n_1,\Sigma)$ 和 $W_2\sim W_p(n_2,\Sigma)$ 相互独立，则 $W_1+W_2\sim W_p(n_1+n_2,\Sigma)$

---

逆威沙特分布

逆威沙特分布是威沙特分布的逆分布，通常用于建模正定对称矩阵的逆矩阵，如果一个随机变量服从于逆伽马分布，记作 $X\sim W_p^{-1}(v,\Psi)$

---

逆威沙特分布的概率密度函数

$f(X\vert v,\Psi)=\frac{\vert\Psi\vert^{v/2}\vert X\vert^{-(v+d+1)/2}\exp(-\frac{1}{2}tr(\Psi X^{-1}))}{2^{vd/2}\Gamma_d(v/2)}$

• $X\in R^{p\times p}$ 是正定矩阵
• $\Psi\in R^{p\times p}$ 是正定矩阵
• $\Gamma_d$ 是多变量伽马分布
• $tr$ 表示矩阵的迹

---

性质

• 如果一个正定矩阵 $W$ 的逆矩阵遵从自由度为 $v$ 的威沙特分布 $W^{-1}\sim W_p(v,\Sigma)$ 的话，那么该矩阵遵从逆威沙特分布 $W\sim W_p^{-1}(v,\Sigma^{-1})$

• 期望 $E[X]=\frac{\Psi}{v-p-1}\quad v>p+1$

• 协方差，对于 $X$ 的元素 $X_{ij},X_{kl}$ ，协方差为

  $Cov(X_{ij},X_{kl}=\frac{(v-p-1)\Psi_{ik}\Psi_{jl}+(v-p-1)\Psi_{il}\Psi_{jk}}{(v-p)(v-p-1)(v-p-3)}\quad v>p+3$

• 逆的期望 $E[X^{-1}]=v\Psi^{-1}$

---

狄利克雷分布

狄利克雷分布（Dirichlet Distribution）是概率论中的一种连续多元概率分布，常用于贝叶斯统计和多元数据分析，它是贝塔分布（Beta Distribution）在高维空间中的推广

---

定义

对于一个 $K$ 维随机向量 $X=\{x_1,…x_k\}$ ，如果其满足如下条件

• 对于任意 $i$ 都满足 $x_i\geq0$
• $\sum_i^Kx_i=1$

并且其概率密度函数为

$f(X\vert\alpha)=\frac{1}{B(\alpha)}\prod_i^Kx_i^{\alpha_i-1}$

• $\alpha=(\alpha_1,…\alpha_K)$ 是一个正实数，称为浓度参数（concentration parameters）
• $B(\alpha)=\frac{\prod_i^K\Gamma(\alpha_i)}{\Gamma(\sum_i^K\alpha_i)}$ 是多元贝塔函数，其中 $\Gamma$ 是伽马函数

---

性质

• 期望值为 $E[x_i]=\frac{\alpha_i}{\sum_j^K\alpha_j}$
• 方差 $Var(x_i)=\frac{\alpha_i(\sum_j^K\alpha_j-\alpha_i)}{(\sum_j^K\alpha_j)^2(\sum_j^K\alpha_j+1)}$
• 协方差为 $Cov(x_i,x_j)=\frac{-\alpha_i\alpha_j}{(\sum_k^K\alpha_k)^2(\sum_k^K\alpha_k+1)}\quad i\neq j$
• 狄利克雷分布是多项分布的共轭先验，即如果先验分布是狄利克雷分布，似然函数是多项分布，那么后验分布也是狄利克雷分布
• 狄利克雷分布具有聚集性质，即对于 $p\sim Dir(\alpha)$ ，则 $p$ 的某些分量可以合并，合并之后仍然是狄利克雷分布
• 当所有的 $\alpha_i$ 相等时，狄利克雷分布是对称的，分布的形状在各个方向上相同

---

贝塔分布

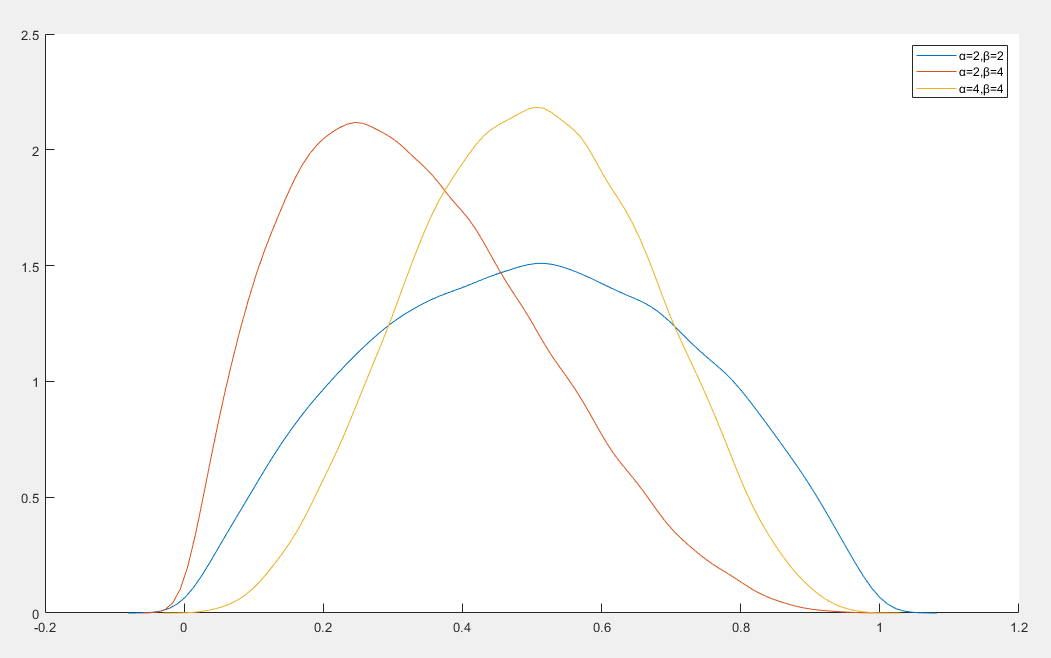
贝塔分布（Beta Distribution）是定义在区间 $[0,1]$ 上的一种连续概率分布，常用于表示概率的概率分布

---

定义

贝塔分布由两个正实数参数 $\alpha$ 和 $\beta$ 定义，其概率密度函数为

$f(x\vert\alpha,\beta)=\frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha,\beta)}$

• $x\in[0,1]$ 是随机变量
• $\alpha>0$ 和 $\beta>0$ 是形状参数
• $B(\alpha,\beta)=\frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}$ 是贝塔函数，其中 $\Gamma$ 是伽马函数

---

性质

• 期望值为 $E[X]=\frac{\alpha}{\alpha+\beta}$
• 方差为 $Var(X)=\frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}$
• 众数为 $Mode(X)=\frac{\alpha-1}{\alpha+\beta-2}$
• 对称性：
  • 当 $\alpha=\beta$ 时分布是对称
  • 当 $\alpha>\beta$ 时分布左偏
  • 当 $\alpha<\beta$ 时分布右偏
• 当 $\alpha=\beta=1$ 时，贝塔分布退化为均匀分布
• 形状
  • 当 $\alpha>1,\beta>1$ 时，分布呈单峰
  • 当 $\alpha<1,\beta<1$ 时，分布呈 U 形
  • 当 $\alpha<1,\beta\geq1$ 或 $\alpha\geq1,\beta<1$ 时，分布呈 J 形

---

多项分布

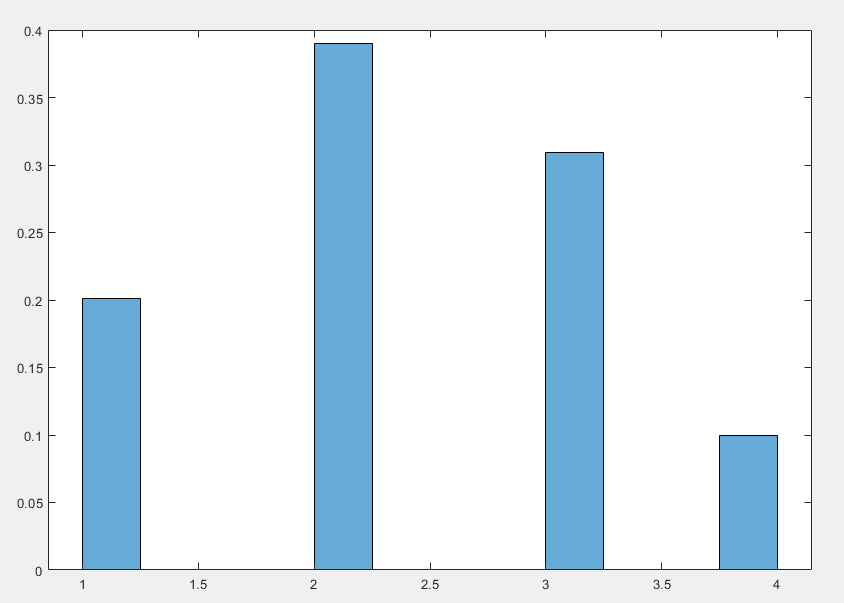
多项分布（Multinomial Distribution）是二项分布的推广，用于描述具有多种可能结果的随机试验

---

定义

多项分布描述了一个随机试验，有 K 种可能，每种结果的概率分别为 $p_1,…p_K$ 进行 $n$ 次独立试验之后，每种结果出现的次数服从多项分布。其概率质量函数如下

$P(x_1,x_2,...x_K)=\frac{n!}{x_1!x_2!...x_K!}p_1^{x_1}p_2^{x_2}...p_K^{x_K}$

• $x_i$ 表示第 $i$ 种结果出现的次数，并且满足 $x_i\geq0,\sum_i^Kx_i=n$
• $p_i$ 是第 $i$ 种结果的概率，满足 $p_i\geq0,\sum_i^Kp_i=1$
• $n$ 是试验总次数

---

性质

• 第 $i$ 种结果期望值为 $E[X_i]=np_i$
• 第 $i$ 种结果的方差为 $Var(X_i)=np_i(1-p_i)$
• 第 $i$ 种结果和第 $j$ 种结果的协方差为 $Cov(X_i,X_j)=-np_ip_j\quad i\neq j$
• 多项分布的边缘分布式二项分布

---

广义极值分布

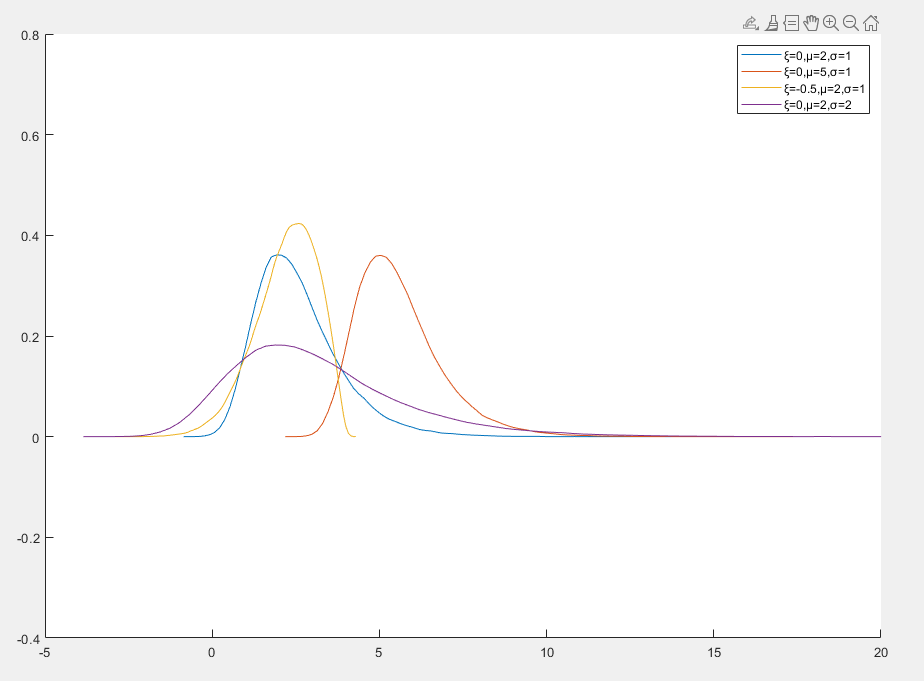
广义极值分布（Generalized Extreme Value Distribution, GEV） 是极值理论中的核心分布，用于描述极端事件（如最大值或最小值）的分布

---

广义极值分布的概率密度函数

$f(x)=\frac{1}{\sigma}\Big[1+\xi(\frac{x-\mu}{\sigma})\Big]^{-1/\xi-1}\exp\bigg\{-\Big[1+\xi(\frac{x-\mu}{\sigma})\Big]^{-1/\xi}\bigg\}$

• $x$ 是随机变量
• $\mu$ 是位置参数
• $\sigma>0$ 是尺度参数
• $\xi$ 是形状参数，决定了分布的尾部行为
  • $\xi>0$ 重尾分布，适合描述极端大值
  • $\xi=0$ 轻尾分布，适合描述中等极端事件
  • $\xi<0$ 有界分布，适合描述极端小值

---

性质

• 期望值为 $E[X]=\mu+\frac{\sigma}{\xi}[\Gamma(1-\xi)-1]\quad\xi<1$
• 方差为 $Var(X)=\frac{\sigma^2}{\xi^2}[\Gamma(1-2\xi)-\Gamma^2(1-\xi)]\quad\xi<0.5$
• 累积分布函数为 $F(x)=\exp\bigg\{-\Big[1+\xi(\frac{x-\mu}{\sigma})\Big]^{-1/\xi}\bigg\}$
• 当 $\xi=0$ 时，广义极值分布退化为 Gumbel 分布
• 当 $\xi>0$ 时，广义极值分布对应于 Frechet 分布
• 当 $\xi<0$ 时，广义极值分布对应于 Weibull 分布

---

Gumbel 分布

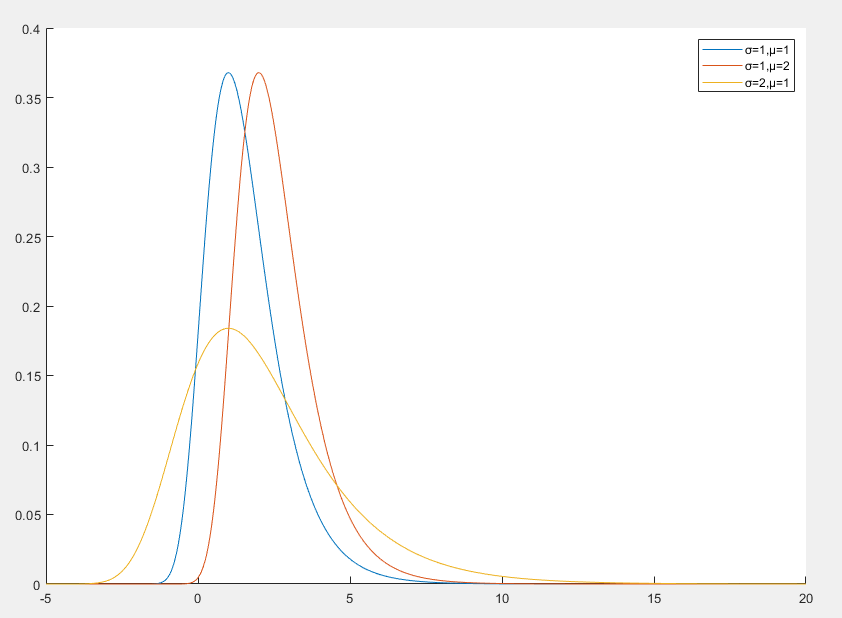
Gumbel 分布 是极值理论中的一种重要分布，用于描述一组独立同分布随机变量的最大值或最小值的分布

---

Gumbel 分布的概率密度函数

$f(x)=\frac{1}{\sigma}\exp\bigg(-\frac{x-\mu}{\sigma}-\exp\Big(-\frac{x-\mu}{\sigma}\Big)\bigg)$

• $x$ 是随机变量
• $\mu$ 是位置参数，决定分布的中心位置
• $\sigma>0$ 是尺度参数，决定分布的宽度

---

性质

• 期望值为 $E[X]=\mu+\sigma\gamma$ ，其中 $\gamma\approx0.5772$ 是欧拉-马歇罗尼常数
• 方差为 $Var(X)=\frac{\pi^2\sigma^2}{6}$
• 累计分布函数为 $F(x)=\exp\bigg(-\exp\Big(-\frac{x-\mu}{\sigma}\Big)\bigg)$
• Gumbel 分布可以看作指数分布的极值分布

---

Frechet 分布

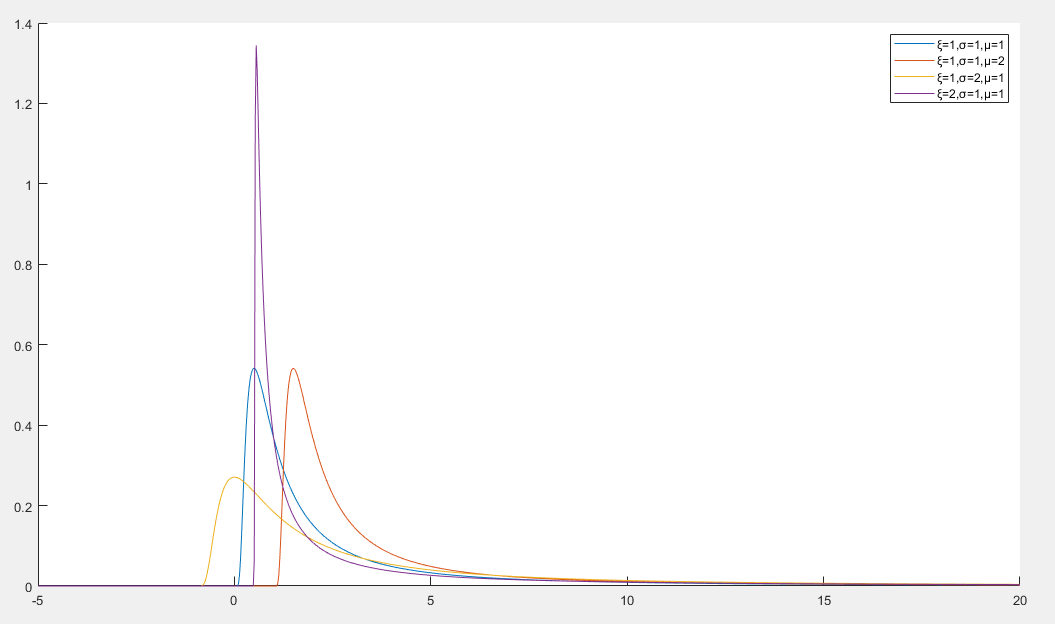
Frechet 分布 是极值理论中的一种重要分布，用于描述一组独立同分布随机变量的最大值的分布

---

Frechet 分布的概率密度函数

$f(x)=\frac{\xi}{\sigma}\Big(\frac{x-\mu}{\sigma}\Big)^{-1-\xi}\exp\bigg(-\Big(\frac{x-\mu}{\sigma}\Big)^{-\xi}\bigg)\quad x>\mu$

• $x$ 是随机变量
• $\xi>0$ 是形状参数，决定分布的尾部行为
• $\sigma>0$ 是尺度参数，决定分布的宽度
• $\mu$ 是位置参数，决定分布下界

---

性质

• 期望值为 $E[X]=\mu+\sigma\Gamma(1-\frac{1}{\xi})\quad\xi>1$ ，其中 $\Gamma$ 是伽马函数
• 方差为 $Var(X)=\sigma^2\Big[\Gamma\Big(1-\frac{2}{\xi}\Big)-\Gamma^2\Big(1-\frac{1}{\xi}\Big)\Big]\quad\xi>2$
• 累积分布函数为 $F(x)=\exp\Big(-\big(\frac{x-\mu}{\sigma}\big)^{-\xi}\Big)\quad x>\mu$

---

Weibull 分布

Weibull 分布是一种连续概率分布

---

Weibull 分布的概率密度函数

$f(x)=\left\{\begin{aligned}&\frac{\xi}{\sigma}\Big(\frac{x}{\sigma}\Big)^{\xi-1}\exp\bigg(-\Big(\frac{x}{\sigma}\Big)^\xi\bigg)&&x\geq0\\&0&&x<0\end{aligned}\right.$

• $x$ 是随机变量，取值为非负值
• $\sigma>0$ 是尺度参数，决定分布的密度
• $\xi>0$ 是形状参数，决定分布的形状
  • $\xi<1$ 分布呈现递减失效率
  • $\xi=1$ 分布退化为指数分布
  • $\xi>1$ 分布呈现递增失效率

---

性质

• 期望值为 $E[X]=\sigma\Gamma(1+\frac{1}{\xi})$
• 方差为 $Var(X)=\sigma^2[\Gamma(1+\frac{2}{\xi})-\Gamma^2(1+\frac{1}{\xi})]$
• 积累分布函数为 $F(x)=\left\{\begin{aligned}&1-\exp\Big(-\big(\frac{x}{\sigma}\big)^\xi\Big)&&x\geq0\\&0&&x<0\end{aligned}\right.$
• 当 $\xi=1$ 时，退化为指数分布
• 当 $\xi=2$ 且 $\sigma=\sqrt{2}\sigma$ 时，退化为瑞利分布

---

帕累托分布

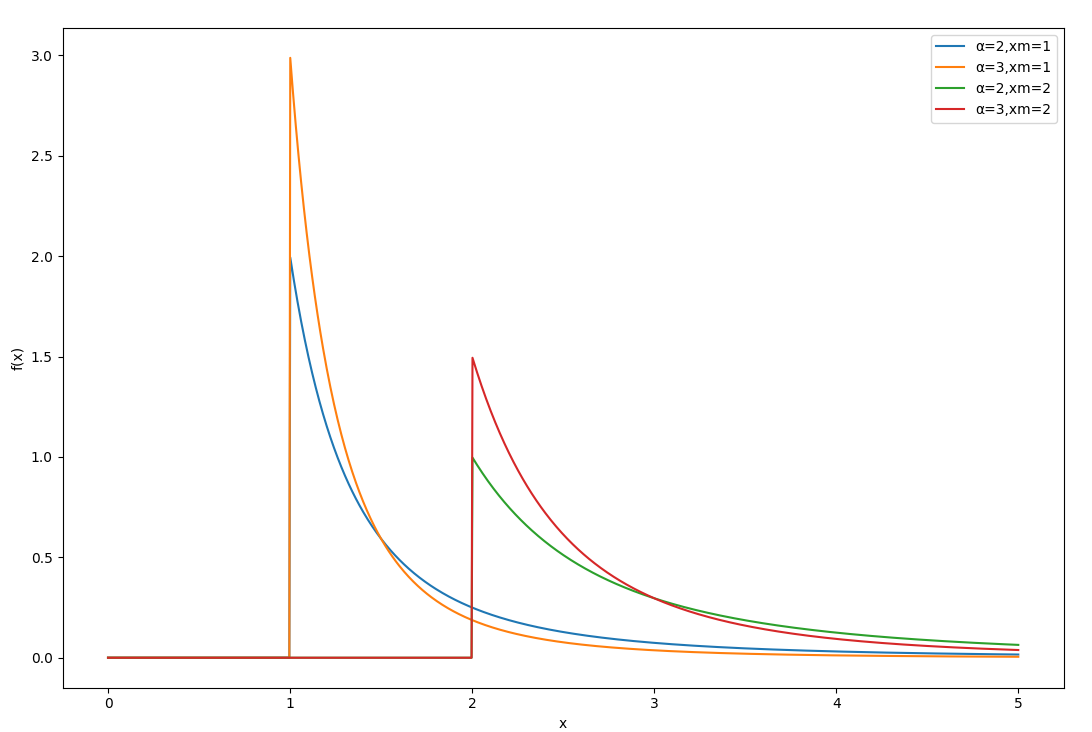
帕累托分布（Pareto Distribution） 是一种连续概率分布，常用于描述具有长尾特性的现象

---

帕累托分布的概率密度函数

$f(x)=\left\{\begin{aligned}&\frac{\alpha x_m^\alpha}{x^{\alpha+1}}&&x\geq x_m\\&0&&x<x_m\end{aligned}\right.$

• $x$ 是随机变量，取值为不小于 $x_m$ 的实数
• $x_m$ 是尺度参数，表示分布的下界
• $\alpha>0$ 是形状参数，决定分布的尾部行为

---

性质

• 期望值为 $E[X]=\left\{\begin{aligned}&\frac{\alpha x_m}{\alpha-1}&&\alpha>1\\&\infty&&\alpha\leq1\end{aligned}\right.$
• 方差为 $Var(X)=\left\{\begin{aligned}&\frac{\alpha x_m^2}{(\alpha-1)^2(\alpha-2)}&&\alpha>2\\&\infty&&\alpha\leq2\end{aligned}\right.$
• 累积分布函数为 $F(x)=\left\{\begin{aligned}&1-\Big(\frac{x_m}{x}\Big)^\alpha&&x\geq x_m\\&0&&x<x_m\end{aligned}\right.$
• 长尾特性：随着 $x$ 的增大，概率密度函数下降得比指数分布更慢
• 当 $x_m=1$ 且 $\alpha\rightarrow\infty$ 时，帕累托分布趋近于指数分布
• 帕累托分布是幂律分布的一种特例

---

广义帕累托分布

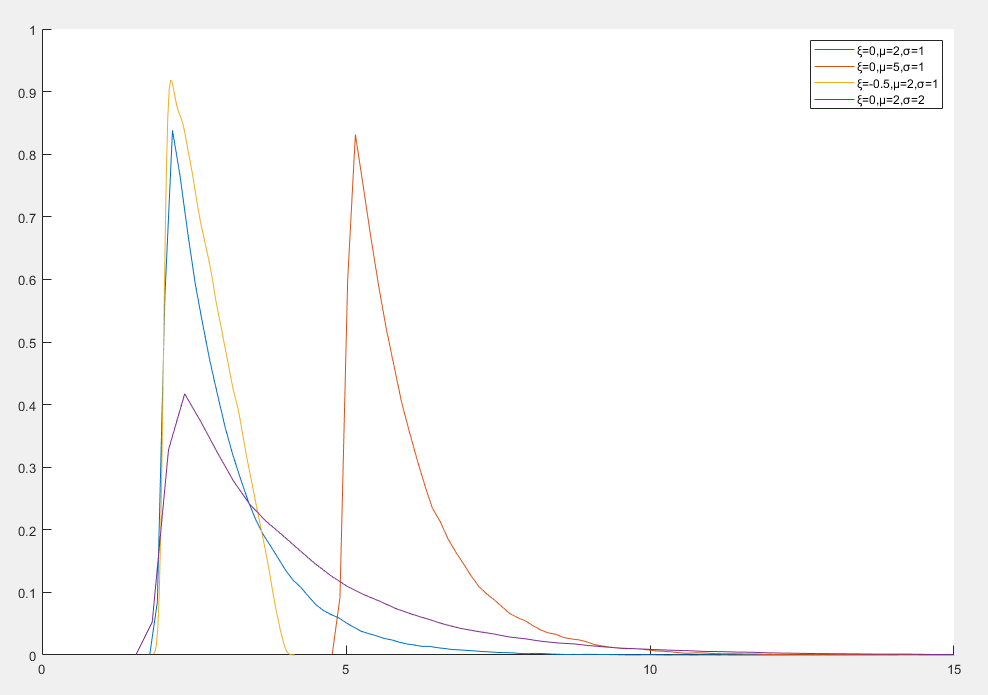
广义帕累托分布（Generalized Pareto Distribution, GPD） 是极值理论中的一种重要分布，用于描述超过某一阈值的极端事件的分布

---

广义帕累托分布的概率密度函数

$f(x)=\left\{\begin{aligned}&\frac{1}{\sigma}(1+\xi\frac{x-\mu}{\sigma})^{-1/\xi-1}&&\xi\neq0\\&\frac{1}{\sigma}\exp(-\frac{x-\mu}{\sigma})&&\xi=0\end{aligned}\right.$

• $x=\left\{\begin{aligned}&[\mu,+\infty)&&\xi\geq0\\&[\mu,\mu-\frac{\sigma}{\xi}]&&\xi<0\end{aligned}\right.$ 是随机变量
• $\mu$ 是位置参数，表示阈值
• $\sigma>0$ 是尺度参数，决定分布的宽度
• $\xi$ 是形状参数，决定分布的尾部行为
  • $\xi>0$ 重尾分布，适合描述极端大值
  • $\xi=0$ 指数衰减尾部，适合描述中等极端事件
  • $\xi<0$ 有界分布，适合描述极端小值

---

性质

• 期望值为 $E[X]=\mu+\frac{\sigma}{1-\xi}\quad\xi<1$
• 方差为 $Var(X)=\frac{\sigma^2}{(1-\xi)^2(1-2\xi)}\quad\xi<0.5$
• $\xi>0$ 且 $\mu=0$ 时，广义帕累托分布退化为帕累托分布
• 当 $\xi=0$ 时，广义帕累托分布退化为指数分布
• 广义帕累托分布是广义极值分布的尾部近似

---

莱维分布

莱维分布（Lévy Distribution） 是一种连续概率分布，属于稳定分布家族，具有重尾特性

---

莱维分布的概率密度函数

$f(x)=\sqrt{\frac{c}{2\pi}}\frac{1}{(x-\mu)^{3/2}}\exp\Big(-\frac{c}{2(x-\mu)}\Big)\quad x>\mu$

• $x>\mu$ 是随机变量
• $\mu$ 是位置参数，表示分布的下界
• $c>0$ 是尺度参数，决定分布的宽度

---

性质

• 期望值为 $E[X]=\infty$
• 方差为 $Var(X)=\infty$
• 莱维分布的期望和方差均为无穷大，表明其具有极端的重尾特性
• 莱维分布是稳定分布的一种特例，满足稳定分布的性质，若 $X_1$ 和 $X_2$ 是独立同分布的莱维随机变量，则 $X_1+X_2$ 也服从莱维分布
• 莱维分布具有重尾特性，其概率密度函数在 $x\rightarrow\mu$ 和 $x\rightarrow\infty$ 时趋近于 0，但下降速度较慢
• 莱维分布是稳定分布的一种特例，稳定分布还包括正态分布和柯西分布
• 柯西分布也是一种重尾分布，但其概率密度函数的下降速度比莱维分布更慢

---

厄密特分布

厄密特分布（Hermite Distribution） 是一种离散概率分布，通常用于描述计数数据中具有过度离散（overdispersion）或零膨胀（zero-inflation）特性的情况

---

厄密特分布的概率质量函数

$P(X=k)=\frac{e^{-\lambda}\lambda^k}{k!}\bigg(1+\alpha\frac{k(k-1)}{\lambda^2}\bigg)$

• $x$ 是随机变量，取值为非负值
• $\lambda>0$ 是分布的均值参数
• $\alpha$ 是形状参数，控制分布的过度离散特性

---

性质

• 期望值为 $E[X]=\lambda$
• 方差值为 $Var(X)=\lambda+2\alpha$
• 当 $\alpha>0$ 时，方差大于均值，表明分布具有过度离散特性
• 当 $\alpha=0$ 时，厄密特分布退化为泊松分布，厄密特分布可以看作是泊松分布的一个扩展，通过引入额外的参数 $\alpha$ 来描述数据的过度离散特性
• 当 $\alpha>0$ 时，厄密特分布的概率质量函数在 $k=0$ 处的值大于泊松分布，表明分布具有零膨胀特性
• 厄密特分布与负二项分布类似，都用于描述过度离散的计数数据

---

博雷尔分布

博雷尔分布（Borel Distribution） 是一种离散概率分布，主要用于描述分支过程（branching processes）中的某些特性，特别是在排队论和随机图理论中有应用

---

博雷尔分布的概率质量函数

$P(X=k)=\frac{e^{-\lambda k}(\lambda k)^{k-1}}{k!}\quad k=1,2,...$

• $X$ 是随机变量，取值为正值
• $\lambda$ 是分布的参数 $0\leq\lambda\leq1$

---

性质

• 期望值为 $E[X]=\frac{1}{1-\lambda}$
• 方差为 $Var(X)=\frac{\lambda}{(1-\lambda)^3}$
• 概率生成函数为 $G(s)=se^{\lambda(G(s)-1)}$
• 博雷尔分布与泊松分布有密切联系，特别是在分支过程和随机图理论中，博雷尔分布描述了某些特定结构的生成
• 当 $\lambda\rightarrow0$ 时，博雷尔分布趋近于几何分布

---

柯西分布

柯西分布（Cauchy Distribution） 是一种连续概率分布，以其重尾特性和缺乏有限的期望和方差而闻名

---

柯西分布的概率密度函数

$f(x)=\frac{1}{\pi\gamma[1+(\frac{x-x_0}{\gamma})^2]}$

• $x\in R$ 是随机变量
• $x_0$ 是位置参数，决定分布的中心位置
• $\gamma>0$ 是尺度参数，决定分布的宽度

---

性质

• 期望值为 $E[X]$ 不存在
• 方差为 $Var(X)$ 不存在
• 柯西分布的期望和方差均为无穷大，表明其具有极端的重尾特性
• 柯西分布是关于 $x=x_0$ 对称的，即 $f(x_0+x)=f(x_0-x)$
• 柯西分布具有重尾特性，其概率密度函数在 $x\rightarrow\plusmn\infty$ 时下降得比正态分布更慢
• 柯西分布是稳定分布的一种特例，满足稳定分布的性质，若 $X_1$ 和 $X_2$ 是独立同分布的柯西随机变量，则 $X_1+X_2$ 也服从柯西分布
• 当自由度 $k=1$ 时，t 分布退化为柯西分布

---

瑞利分布

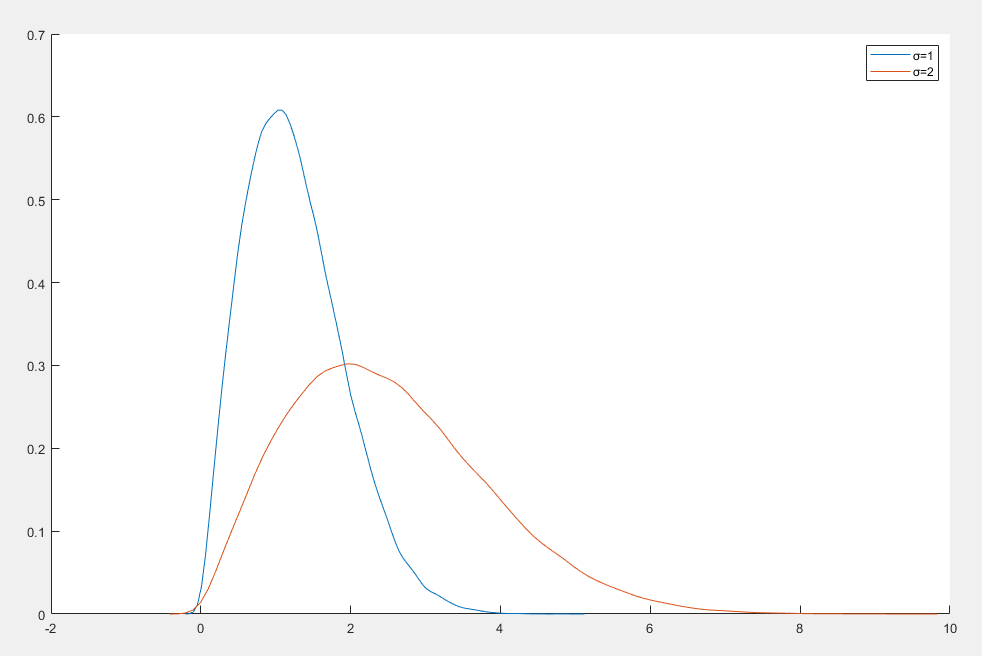
瑞利分布（Rayleigh Distribution） 是一种连续概率分布，通常用于描述二维空间中随机向量的模的分布

---

瑞利分布的概率密度函数

$f(x)=\frac{x}{\sigma^2}\exp(-\frac{x^2}{2\sigma^2})\quad x\geq0$

• $x$ 是随机变量，取值为非负实数
• $\sigma>0$ 是尺度参数，决定分布的宽度

---

性质

• 期望值为 $E[X]=\sigma\sqrt{\frac{\pi}{2}}$
• 方差为 $Var(X)=\sigma^2(2-\frac{\pi}{2})$
• 累积分布函数为 $F(x)=1-\exp(-\frac{x^2}{2\sigma^2})\quad x\geq0$
• 瑞利分布可以看作是两个独立同分布的正态随机变量的模的分布，即对于两个独立同分布的正态随机变量 $X,Y\sim\mathcal{N}(0,\sigma^2)$ ，则 $Z=\sqrt{X^2+Y^2}\sim Rayleigh(\sigma)$
• 瑞利分布的平方服从指数分布，即若 $X\sim Rayleigh(\sigma)$ 则 $X^2\sim Exponential(\lambda=\frac{1}{2\sigma^2})$

---

幂律分布

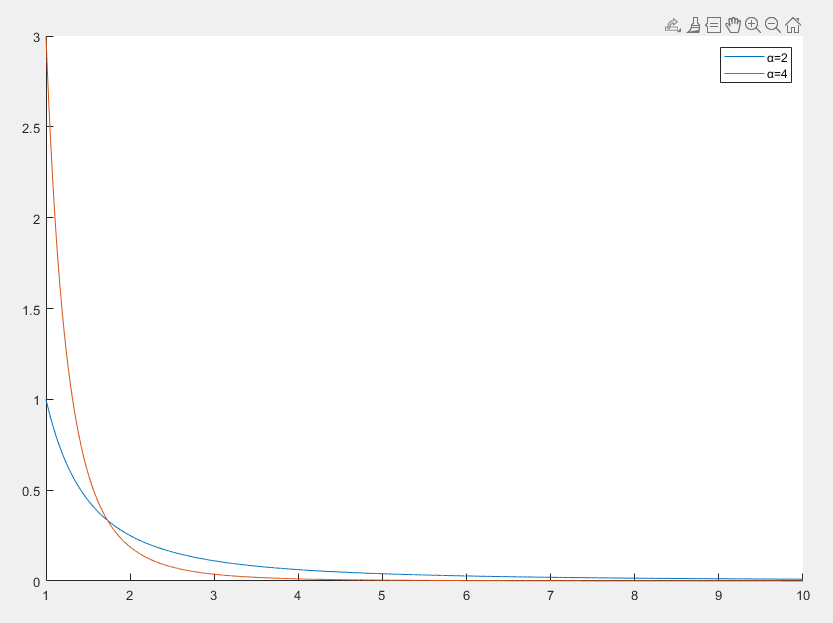
幂律分布（Power-law Distribution） 是一种描述许多自然和社会现象中重尾特性的概率分布

---

幂律分布的概率密度函数

$f(x)=Cx^{-\alpha}\quad x\geq x_{\min}$

• $x$ 是随机变量
• $\alpha>1$ 是幂律指数，决定分布的尾部行为
• $C$ 是归一化常数，满足 $\int_{x_{min}}^\infty f(x)dx=1$

归一化常数计算之后得到 $C=(\alpha-1)x_{\min}^{\alpha-1}$ ，幂律分布的概率密度函数可以表示为

$f(x)=\frac{\alpha-1}{x_{\min}}\bigg(\frac{x}{x_{\min}}\bigg)^{-\alpha}\quad x\geq x_{\min}$

---

性质

• 期望值为 $E[X]=\frac{\alpha-1}{\alpha-2}x$
• 方差为 $Var(X)=\frac{\alpha-1}{(\alpha-2)(\alpha-3)}x_{\min}^2\quad\alpha>3$
• 当 $\alpha\leq2$ 时期望不存在， $\alpha\leq3$ 方差不存在
• 幂律分布具有重尾特性，即随着 $x$ 的增大，概率密度函数下降得比指数分布更慢，这种特性使得幂律分布适合描述极端事件或稀有事件
• 幂律分布具有尺度不变性，即对于任意常数 $c>0$ 有 $f(cx)=c^{-\alpha}f(x)$
• 帕累托分布是幂律分布的一种特例，当 $x_{\min}>0$ 时，幂律分布退化为帕累托分布
• 当 $\alpha\rightarrow\infty$ 时幂律分布趋近于指数分布

---

三角分布

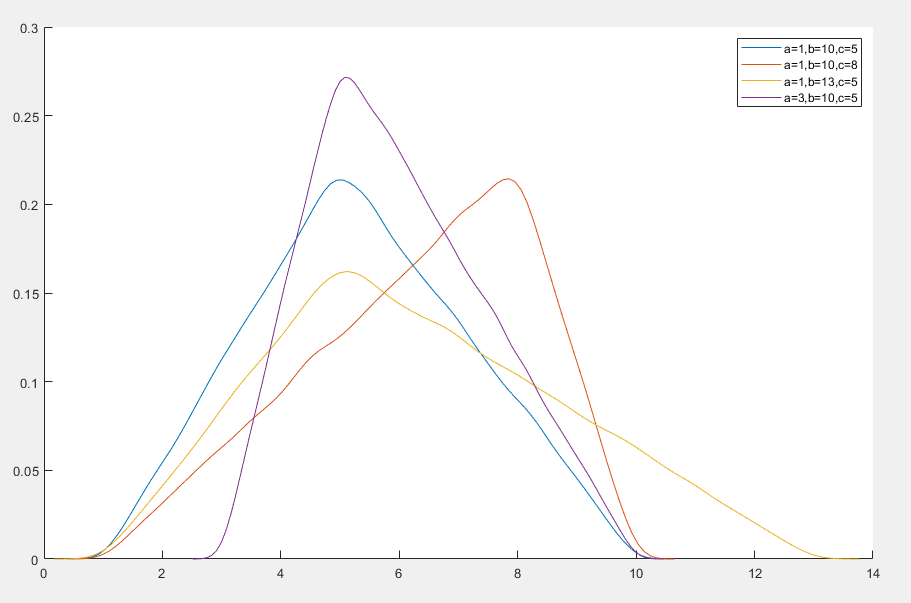
三角分布（Triangular Distribution）是一种连续概率分布，常用于描述在已知最小值、最大值和众数的情况下，随机变量的分布情况

---

三角分布的概率密度函数

$f(x)=\left\{\begin{aligned}&\frac{2(x-a)}{(b-a)(c-a)}&&a\leq x\leq c\\&\frac{2(b-x)}{(b-a)(b-c)}&&c<x\leq b\\&0\end{aligned}\right.$

• $a$ 是最小值，是下限
• $b$ 是最大值，上限
• $c$ 是众数，取值范围为 $[a,b]$

---

性质

• 期望值为 $E[X]=\frac{a+b+c}{3}$
• 方差为 $Var(X)=\frac{a^2+b^2+c^2-ab-ac-bc}{18}$
• 概率密度函数呈三角形
• 当 $c=\frac{a+b}{2}$ 分布是对称的

---

分段线性分布

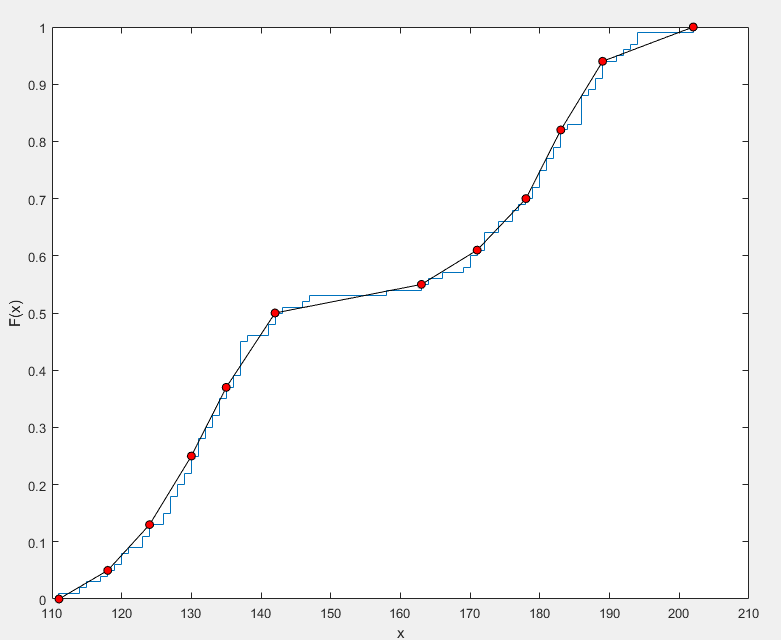
分段线性分布（Piecewise Linear Distribution）是一种通过分段线性函数定义的连续概率分布，其概率密度函数（PDF）由多个线性段组成，通常用于描述具有不同变化趋势的随机变量

---

分段线性分布的概率密度函数

分段线性分布的概率密度函数由多个线性段组成，每个段在定义域的不同区间内具有不同的斜率，通常，分段线性分布的定义域被划分为若干区间，每个区间内的概率密度函数是线性的

$f(x)=\left\{\begin{aligned}&m_1x+b_1&&x_0\leq x\leq x_1\\&m_2x+b_2&&x_1\leq x\leq x_2\\&...\\&m_nx+b_n&&x_{n-1}\leq x\leq x_n\\&0\end{aligned}\right.$

• $m_i$ 是第 $i$ 段的斜率
• $b_i$ 是第 $i$ 段的截距

---

性质

• 期望值为 $E[X]=\int xf(x)dx$
• 方差为 $Var(X)=E(X^2)-[E(X)]^2$
• 非负性： $\forall x\Rightarrow f(x)\geq0$
• 归一性：整个定义域上的积分为 1， $\int f(x)dx=1$
• 通过调整分段区间的斜率和截距，可以灵活地描述复杂的分布形状
• 由于概率密度函数是线性的，计算期望值和方差时可以使用分段积分

---

t 位置尺度分布

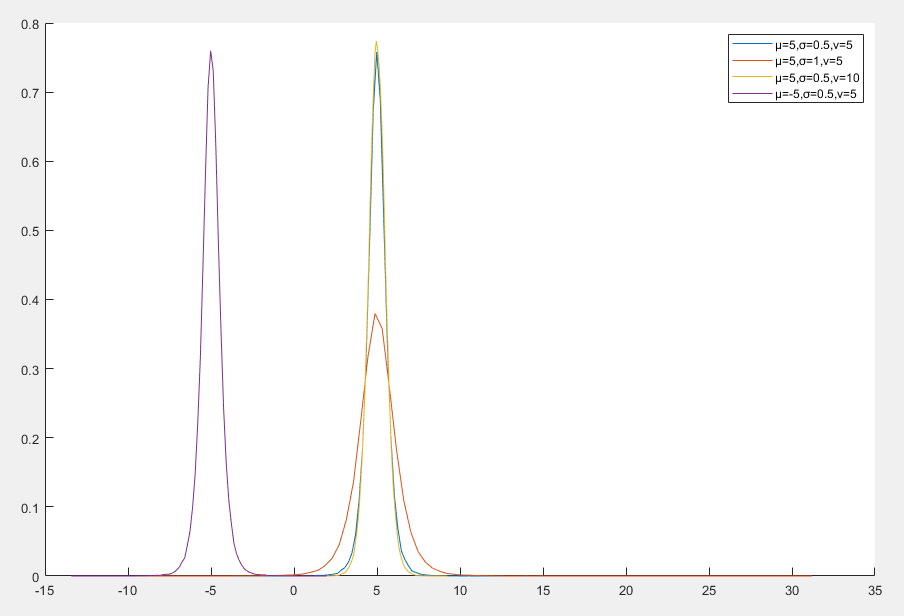
t 位置尺度分布（t Location-Scale Distribution）是统计学中的一种连续概率分布，它是 t 分布 的推广形式，通过引入位置参数和尺度参数，使其更具灵活性。t 位置尺度分布在处理具有重尾特性的数据时非常有用，尤其是在数据中存在异常值或偏离正态分布的情况下

---

t 位置尺度分布的概率密度函数

$f(x)=\frac{\Gamma(\frac{v+1}{2})}{\sigma\sqrt{v\pi}\Gamma(\frac{v}{2})}(1+\frac{1}{v}(\frac{x-\mu}{\sigma})^2)^{-\frac{v+1}{2}}$

• $\mu$ 是位置参数，分布的均值或中心位置
• $\sigma>0$ 是尺度参数，分布的标准差或尺度
• $v>0$ 是自由度参数，控制分布的尾部厚度
  • 自由度越小，尾部越厚
  • 自由度越大，分布越接近正态分布

---

性质

• 期望值为 $E[X]=\mu\quad v>1$
• 方差为 $Var(X)=\sigma^2\frac{v}{v-2}\quad v>2$
• 当 $v\leq1$ 时，期望值不存在
• 当 $v\leq2$ 时，方差不存在
• 累积分布函数为 $F(x)=\int_{-\infty}^xf(t)dt$
• t 位置尺度分布的尾部比正态分布更厚，能够更好地捕捉异常值
• 通过调整自由度参数，可以控制分布的尾部厚度
• 在处理非正态数据时，t 位置尺度分布比正态分布更具鲁棒性

---

逻辑分布

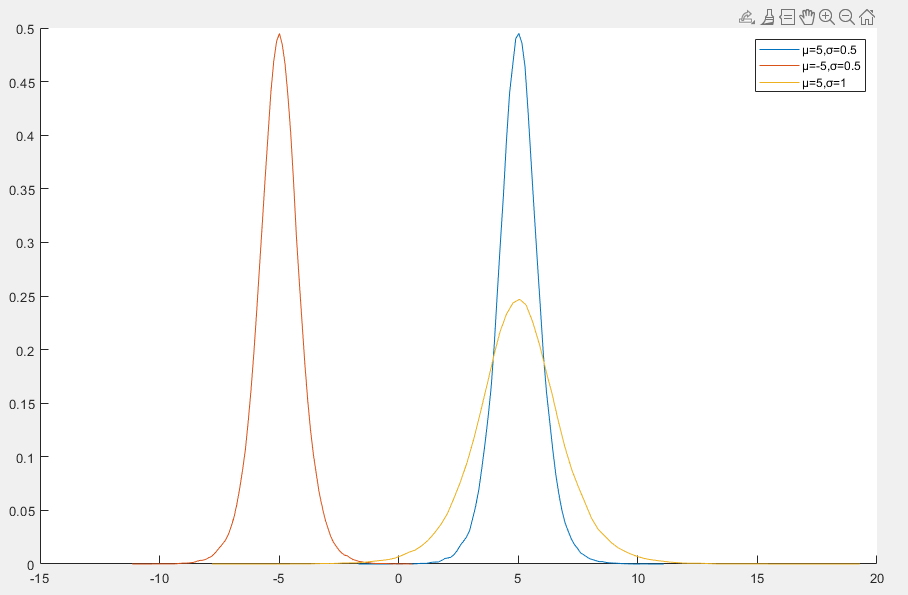
逻辑分布（Logistic Distribution）是一种连续概率分布，常用于统计学和机器学习中的分类问题，它的形状与正态分布类似，但具有更厚的尾部

---

逻辑分布的概率密度函数

$f(x)=\frac{e^{-\frac{x-\mu}{s}}}{s(1+e^{-\frac{x-\mu}{s}})^2}$

• $\mu$ 是位置参数，分布的中位数和均值
• $s>0$ 是尺度参数，控制分布的宽度

---

性质

• 期望值为 $E[X]=\mu$
• 方差为 $Var(X)=\frac{s^2\pi^2}{3}$
• 累积分布函数为 $F(x)=\frac{1}{1+e^{-\frac{x-\mu}{s}}}$
• 逻辑分布的形状与正态分布类似，但尾部更厚，能够更好地捕捉极端值
• 逻辑分布是关于位置参数 $\mu$ 对称的
• 逻辑分布的峰度比正态分布更高

---

半正态分布

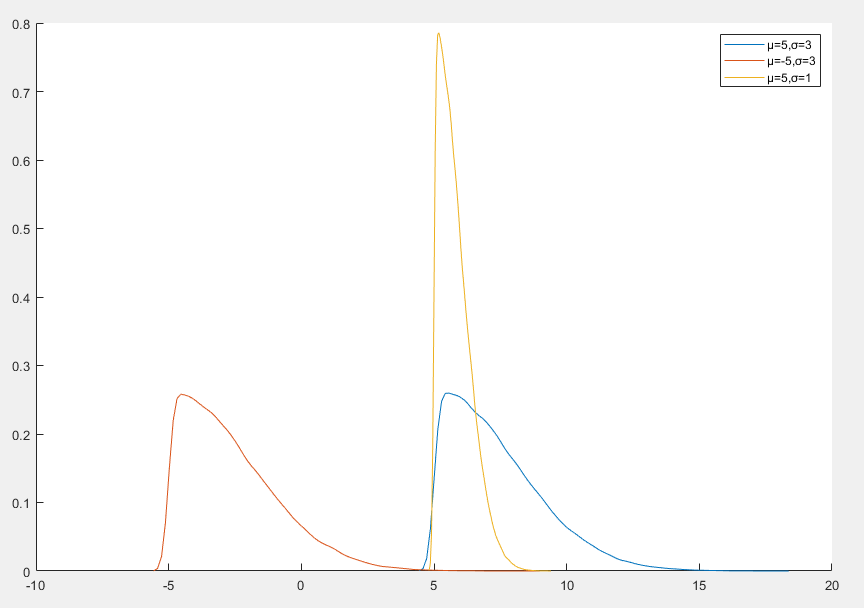
半正态分布（Half-Normal Distribution）是一种连续概率分布，它是将正态分布限制在非负实数域

---

半正态分布的概率密度函数

$f(x)=\frac{\sqrt{2}}{\sigma\sqrt{\pi}}\exp(-\frac{x^2}{2\sigma^2})\quad x\geq0$

• $\sigma$ 是尺度参数

---

性质

• 期望值为 $E[X]=\sigma\sqrt{\frac{2}{\pi}}$
• 方差为 $Var(X)=\sigma^2(1-\frac{2}{\pi})$
• 累积分布函数为 $F(x)=erf(\frac{x}{\sigma\sqrt{2}})\quad x\geq0$ 其中 $erf(z)=\frac{2}{\sqrt{\pi}}\int^z_0e^{-t^2}dt$ 是误差函数
• 半正态分布仅定义在非负实数域上
• 半正态分布的形状是单峰的，峰值位于 $x=0$ 处
• 半正态分布是正态分布在 $x\geq0$ 上的截断

---

伯恩鲍姆-桑德斯分布

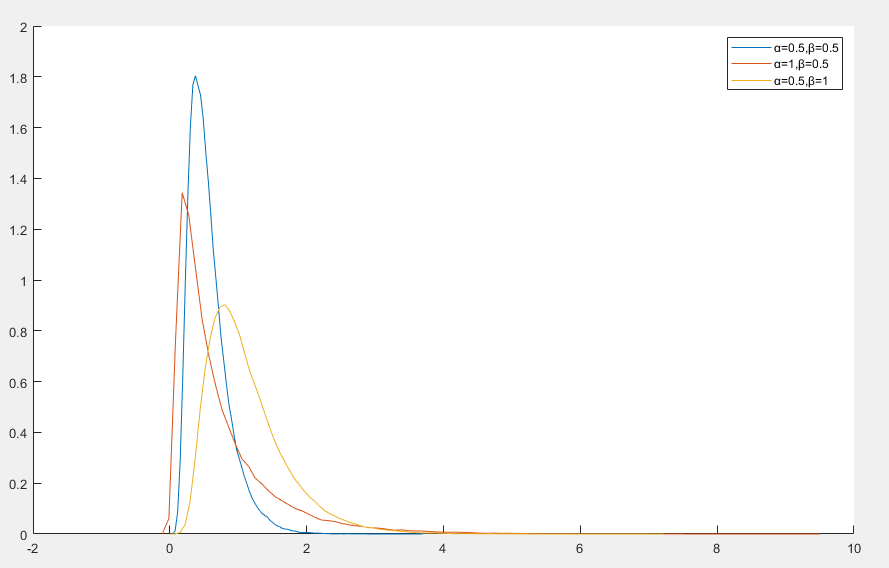
伯恩鲍姆-桑德斯分布（Birnbaum-Saunders Distribution）是一种用于描述材料疲劳寿命的概率分布

---

伯恩鲍姆-桑德斯分布的概率密度函数

$f(x)=\frac{1}{2\alpha\beta}\Big(\frac{\beta}{x}+\sqrt{\frac{\beta}{x}}\Big)\exp\Big(-\frac{1}{2\alpha^2}\Big(\frac{x}{\beta}+\frac{\beta}{x}-2\Big)\Big)\quad x>0$

• $x$ 是随机变量，通常用来表示失效时间或寿命
• $\alpha>0$ 是形状参数，控制分布的偏度和尾部厚度
  • 较小值使分布更对称
  • 较大值使分布更偏斜
• $\beta>0$ 是尺度参数，决定分布的中心，是分布的中位数，即 $p(x\leq\beta)=0.5$

---

性质

• 均值为 $E[X]=\beta(1+\frac{\alpha^2}{2})$
• 方差为 $Var(X)=(\alpha\beta)^2(1+\frac{5\alpha^2}{4})$
• 累积分布函数为 $F(x)=\Phi(\frac{1}{\alpha}(\sqrt{\frac{x}{\beta}}-\sqrt{\frac{\beta}{x}}))$

---

Nakagami 分布

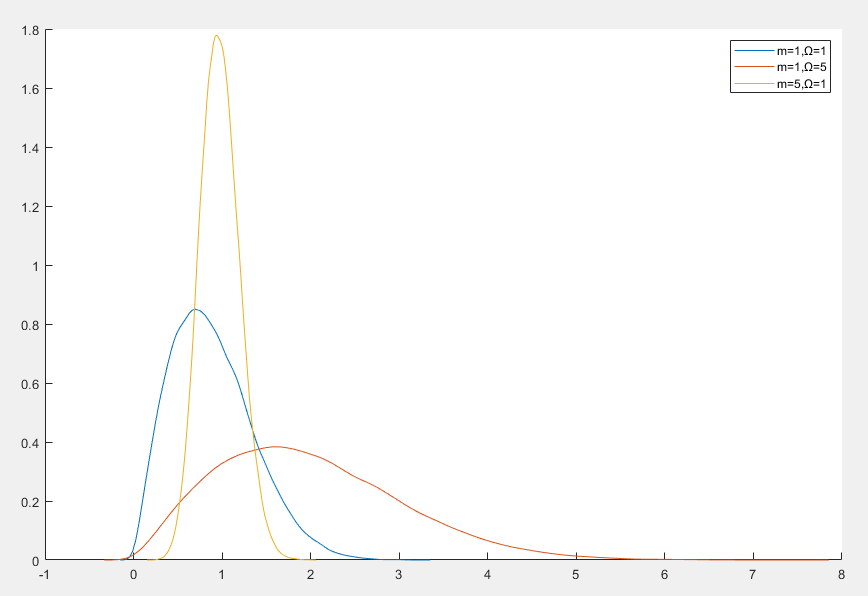
Nakagami 分布（Nakagami Distribution）是一种连续概率分布，常用于无线通信领域，特别是用于建模无线信道的衰落特性

---

Nakagami 分布的概率密度函数

$f(x)=\frac{2m^m}{\Gamma(m)\Omega^m}x^{2m-1}\exp(-\frac{mx^2}{\Omega})\quad x\geq0$

• $m\geq0.5$ 是形状参数，控制分布的形状
• $\Omega>0$ 是尺度参数，控制分布的尺度

---

性质

• 期望值为 $E[X]=\frac{\Gamma(m+\frac{1}{2}}{\Gamma(m)}\sqrt{\frac{\Omega}{m}}$
• 方差为 $Var(X)=\Omega(1-\frac{1}{m}(\frac{\Gamma(m+\frac{1}{2})}{\Gamma(m)})^2)$
• 累积分布函数为 $F(x)=\frac{\gamma(m,\frac{mx^2}{\Omega})}{\Gamma(m)}\quad x\geq0$
• 当 $m=1$ 时 Nakagami 分布退化为瑞利分布
• 当 $m=0.5$ 时 Nakagami 分布退化为单边高斯分布
• Nakagami 分布可以拟合从轻度到重度的衰落信道
• Nakagami 分布仅定义在非负实数域上

---

莱斯分布

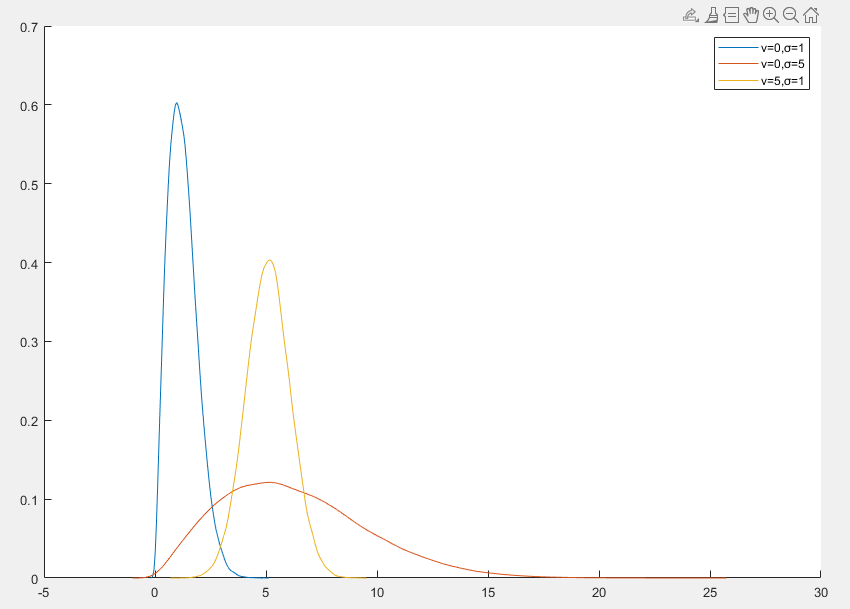
莱斯分布（Rice Distribution）是一种连续概率分布，常用于描述存在主导信号（如直射路径）的随机信号的幅度分布

---

莱斯分布的概率密度函数

$f(x)=\frac{x}{\sigma^2}\exp(-\frac{x^2+v^2}{2\sigma^2})I_0(\frac{xv}{\sigma^2})\quad x\geq0$

• $v\geq0$ 是非中心参数，主导信号的幅度，较大时分布更集中于主导信号附近
• $\sigma>0$ 是尺度参数，散射信号的强度
• $I_0$ 是零阶修正贝塞尔函数

---

性质

• 期望值为 $E[X]=\sigma\sqrt{\frac{\pi}{2}}L_{1/2}(-\frac{v^2}{2\sigma^2})$ 其中 $L_{1/2}$ 是拉盖尔多项式
• 方差为 $Var(X)=2\sigma^2+v^2-[\sigma\sqrt{\frac{\pi}{2}}L_{1/2}(-\frac{v^2}{2\sigma^2})]^2$
• 累积分布函数为 $F(x)=1-Q_1(\frac{v}{\sigma},\frac{x}{\sigma})\quad x\geq0$ ，其中 $Q_1(a,b)=\int_b^\infty t\exp(-\frac{t^2+a^2}{2})I_0(at)dt$ 是马库姆 Q 函数
• 当 $v=0$ 时，莱斯分布退化为瑞利分布
• 莱斯分布仅定义在非负实数域上

---

稳定分布

稳定分布（Stable Distribution）是一类重要的概率分布，具有稳定性和广义中心极限定理的特性

---

稳定分布的特征函数

稳定分布的概率密度函数通常没有闭式表达式，但其特征函数可以显式表示

$\phi(x)=\exp\{ix\delta-\gamma^\alpha\vert x\vert^\alpha(1-i\beta sgn(x)w(x,\alpha))\}$

• $0<\alpha\leq2$ 稳定性参数，控制分布的尾部厚度
• $-1\leq\beta\leq1$ 偏度参数，控制分布的对称性
• $\gamma<0$ 尺度参数，控制分布的尺度
• $\delta$ 位置参数，控制分布的位置
• $sgn(x)$ 是符号函数
• $w(x,\alpha)=\left\{\begin{aligned}\tan(\frac{\pi\alpha}{2})&&\alpha\neq1\\-\frac{2}{\pi}\log\vert t\vert&&\alpha=1\end{aligned}\right.$ 是一个与参数 $\alpha$ 相关的函数

---

性质

• 当 $1<\alpha\leq2$ 时，期望值为 $\delta$ ，否则期望值不存在
• 当 $\alpha<2$ 时，稳定分布的方差不存在，当 $\alpha=2$ 时，方差为 $2\gamma^2$
• 稳定性：如果两个独立且服从稳定分布的随机变量 $X_1$ 和 $X_2$ ，则对于任意常数 $a,b>0$ ，存在常数 $c$ 和 $d$ ，使得 $aX_1+bX_2\sim cX+d$ ，其中 $X$ 也服从稳定分布
• 广义中心极限定理：对于独立同分布的随机变量，其标准化和的极限分布是稳定分布
• 当 $\alpha=2$ 时，稳定分布退化为正态分布，此时 $\beta$ 无效
• 当 $\alpha=1$ 且 $\beta=2$ 时，稳定分布退化为柯西分布
• 当 $\alpha=0.5$ 且 $\beta=1$ 时，稳定分布退化为莱维分布

---

伯尔分布

伯尔分布（Birnbaum-Saunders Distribution），也称为疲劳寿命分布，是一种连续概率分布，常用于描述材料的疲劳寿命或失效时间

---

伯尔分布的概率密度函数

$f(x)=\frac{1}{2\alpha\beta}(\frac{x}{\beta}+\frac{\beta}{x})\exp(-\frac{1}{2\sigma^2}(\frac{x}{\beta}+\frac{\beta}{x}-2))\quad x>0$

• $\alpha>0$ 是形状参数，控制分布的偏度和尾部厚度
• $\beta>0$ 是尺度参数，控制分布的位置和尺度

---

性质

• 期望值为 $E[X]=\beta(1+\frac{\alpha^2}{2})$
• 方差为 $Var(X)=(\alpha\beta)^2(1+\frac{5\sigma^2}{4})$
• 累积分布函数为 $F(x)=\Phi(\frac{1}{\alpha}(\sqrt{\frac{x}{\beta}}-\sqrt{\frac{\beta}{x}}))\quad x>0$ ，其中 $\Phi$ 是标准正态分布的累积分布函数
• 伯尔分布仅定义在正实数域上
• 伯尔分布是右偏的

---