前言

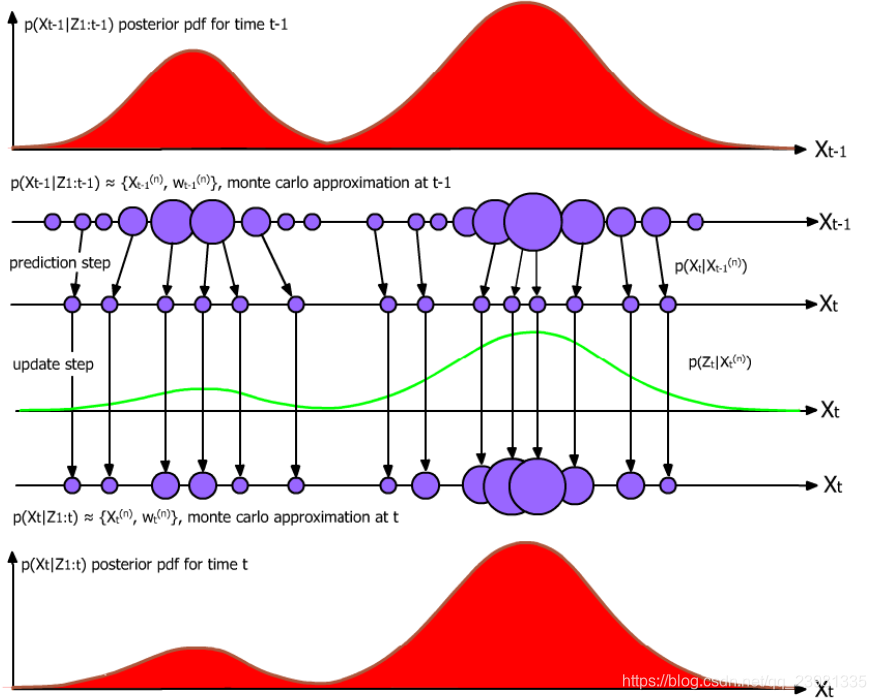
对于一般的非线性/非高斯系统,解析求解的途径是行不通的。在数值近似方法中，蒙特卡罗仿真是一种最为通用、有效的手段，粒子滤波就是建立在蒙特卡罗仿真基础之上的，它通过利用一组带权值的系统状态采样来近似状态的统计分布。由于蒙特卡罗仿真方法具有广泛的适用性，由此得到的粒子滤波算法也能适用于一般的非线性/非高斯系统。但是，这种滤波方法也面临几个重要问题，如有效采样(粒子)如何产生、粒子如何传递以及系统状态的序贯估计如何得到等。

简单的理解，粒子滤波就是使用了大量的随机样本，采用 蒙特卡洛(MonteCarlo，MC)仿真技术完成 贝叶斯递推滤波 (Recursive Bayesian Filter) 过程。

一阶矩 mean

一阶矩是随机变量的期望值

μ=E[X]=∑p(xi)xi\mu=E[X]=\sum p(x_i)x_i

二阶矩 variance

二阶矩是随机变量偏离其期望值的平方的期望值，表示随机变量的离散程度

σ2=E[(X−μ)2]=∑p(xi)(xi−μ)2\sigma^2=E[(X-\mu)^2]=\sum p(x_i)(x_i-\mu)^2

三阶矩 skewness

三阶矩是随机变量偏离其期望值的立方的期望值，表示随机变量分布的偏斜程度

γ=E[(X−μ)3]=∑p(xi)(xi−μ)3\gamma=E[(X-\mu)^3]=\sum p(x_i)(x_i-\mu)^3

提议分布

在粒子滤波器中，提议分布的选择很重要，直接影响粒子的采样效率和估计精度，对于不同形式的提议分布，滤波器的性能也会不同

  • 选择先验分布作为提议分布 q(xk∣xk−1i,yk)=p(xk∣xk−1i)q(x_k|x_{k-1}^i,y_k)=p(x_k|x_{k-1}^i)
  • 最优提议分布，即选择最小化权重方差的分布 q(xk∣xk−1i,yk)=p(xk∣xk−1i,yk)q(x_k|x_{k-1}^i,y_k)=p(x_k|x_{k-1}^i,y_k)
  • 扩展提议分布，使用近似的方式（例如无迹变换）构造更接近真实后验的提议分布

蒙特卡洛采样方法

  • 直接采样，根据概率分布进行采样，需要已知概率密度函数与累积概率密度函数的概率分布
  • 接收-拒绝采样，对于累积分布函数未知的分布，采用提议分布 q(x)q(x) 且使 kq(x)≥p(x)kq(x)\geq p(x) ，首先在 kq(x)kq(x) 中按照直接采样的方法采样粒子，如果落到 p(x)p(x) 内时，接收这个粒子，否则拒绝这个粒子
  • 重要性采样，在提议分布 q(x)q(x) 中采样大量粒子，设置每个粒子的权重为 p(xi)q(xi)\frac{p(x_i)}{q(x_i)}

粒子滤波器

系统描述

对于一个离散的开环系统

xk=Axk−1+Gwk−1zk=Cxk+Hvkx_k=Ax_{k-1}+Gw_{k-1}\\z_k=Cx_k+Hv_k

其中 xkx_k 为 k 时刻的系统状态向量， zkz_k 为 k 时刻的测量输出向量，这里是一个开环系统，不考虑系统的输入 uu。 wk,vkw_k,v_k 分别是系统过程噪声和观测噪声，并且均为零均值高斯白噪声。犹豫贝叶斯滤波的递推形式是基于非线性系统的后验概率密度，因此这里并不需要假设噪声均为零均值白噪声。但是对于 KF，EKF，CKF，QKF 等需要假设过程噪声和测量噪声均为零均值高斯白噪声。因此基于贝叶斯滤波的粒子滤波可以处理非线性非高斯的状态估计问题。

定义 1∼k1\sim k 时刻的 xkx_k 的所有测量数据为

z1:k=[z1Tz2T...zkT]Tz_{1:k}=\begin{bmatrix}z_1^T&z_2^T&...&z_k^T\end{bmatrix}^T

贝叶斯滤波问题就是计算 k 时刻状态 x 估计的置信程度，为此构造概率密度函数 p(xk∣zk)p(x_k|z^k) ，在给定初始分布 p(x0∣z0)=p(x0)p(x_0|z^0)=p(x_0) 之后，从理论上看，可以通过预测和更新两个步骤递推得到概率密度函数 p(xk∣zk)p(x_k|z^k) 的值，有点 KF 的样子。

贝叶斯滤波简述

预测步 p(xk−1∣y1:k−1)→p(xk∣y1:k−1)p(x_{k-1}|y_{1:k-1})→p(x_k|y_{1:k-1}) ，根据在 k−1k-1 时刻得到的后验概率来估计 xkx_k 的概率

p(xk∣y1:k−1)=∫p(xk∣xk−1)p(xk−1∣y1:k−1)dxk−1p(x_k|y_{1:k-1})=\int{p(x_k|x_{k-1})p(x_{k-1}|y_{1:k-1})dx_{k-1}}

更新步 p(xk∣y1:k−1)→p(xk∣y1:k)p(x_k|y_{1:k-1})→p(x_k|y_{1:k}) ，根据观测到得数据 yky_k 来更新数据，得到 kk 时刻的后验概率

p(xk∣y1:k)=p(yk∣xk)p(xk∣y1:k−1)p(yk∣y1:k−1)p(yk∣y1:k−1)=∫p(yk∣xk)p(xk∣y1:k−1)dxkp(x_k|y_{1:k})=\frac{p(y_k|x_k)p(x_k|y_{1:k-1})}{p(y_k|y_{1:k-1})}\\p(y_k|y_{1:k-1})=\int{p(y_k|x_k)p(x_k|y_{1:k-1})dx_k}

实际上各种滤波，估计就是求解 p(xk∣y1:k)p(x_k|y_{1:k}) 的一阶矩（ xkx_k 的估计）以及二阶矩（估计的协方差），其中 y1:k−1y_{1:k-1} 是在 k−1k-1 时刻时所得到的所有观测数据，即 y1:k−1=[y1,⋯ ,yk−1]y_{1:k-1}=[y_1,\cdots,y_{k-1}]

上述的更新步公式描述了由 k−1k − 1 时刻后验概率密度函数向 kk 时刻后验概率密度函数递推的完整过程，从而构成了贝叶斯估计最优解的通用表示形式。进而通过后验分布 p(xk∣z1:k)p(x_k|z_{1:k}) 可以得到不同准则条件下 x 的最优估计计划。

例如：

  • 最小均方误差MMSE估计为

    x^k=E(xk∣zk)=∫xkp(xk∣y1:k)dxk\hat{x}_k=E(x_k|z_k)=\int{x_kp(x_k|y_{1:k})}dx_k

  • 最大后验MAP估计为

    x^k=arg⁡max⁡xk p(xk∣y1:k)\hat{x}_k=\arg\underset{x_k}{\max}~p(x_k|y_{1:k})

实际上粒子滤波就是基于蒙特卡洛技术，将上述递推的过程用大量采样的方式实现了

标准的粒子滤波PF

核心思想是使用一组具有相应权值的随机样本(粒子)来表示状态的后验分布。

该方法的基本思路是选取一个重要性概率密度并从中进行随机抽样，得到一些带有相应权值的随机样本后，在状态观测的基础上调节权值的大小和粒子的位置，再使用这些样本来逼近状态后验分布，最后将这组样本的加权求和作为状态的估计值。粒子滤波不受系统模型的线性和高斯假设约束，采用样本形式而不是函数形式对状态概率密度进行描述，使其不需要对状态变量的概率分布进行过多的约束，因而在非线性非高斯动态系统中广泛应用。尽管如此，粒子滤波目前仍存在计算量过大、粒子退化等关键问题亟待突破。粒子滤波实际上是上述基于贝叶斯滤波的最小均方误差 MMSE 估计的近似实现，而近似方法就是蒙特卡洛方法。

通常选择先验分布作为重要性密度函数（重要性的提议分布），即

q(xk∣xk−1i,yk)=p(xk∣xk−1i)q(x_k|x_{k-1}^{i},y_k)=p(x_k|x_{k-1}^i)

对该函数取重要性权值为

wki=wk−1ip(yk∣xki)p(xki∣xk−1i)q(xki∣xk−1i,yk)=wk−1ip(yk∣xki)w_k^i=w_{k-1}^i\frac{p(y_k|x_k^i)p(x_k^i|x_{k-1}^i)}{q(x_k^i|x_{k-1}^{i},y_k)}=w_{k-1}^ip(y_k|x_k^i)

该权值需要归一化为 w‾ki\overline{w}_k^i

步骤

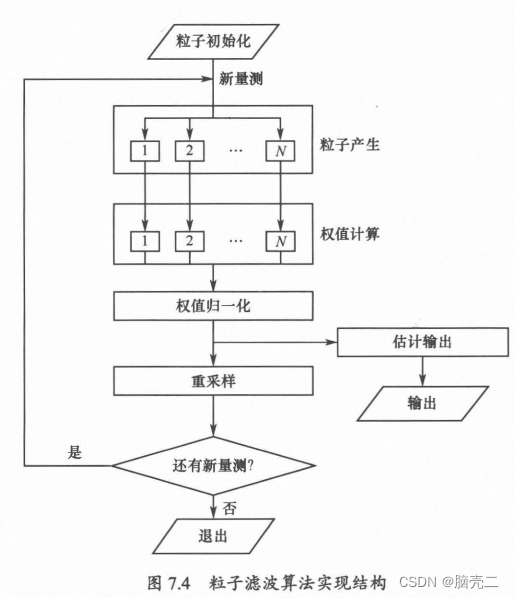
420a2bd9b5e14a558dea20fd5b4f7bb2.png

  1. 初始时根据先验分布 p(x0)p(x_0) 采样得到 N 个粒子 x0i∼p(x0)x_0^i\sim p(x_0) ，并且初始化权重 w0i=1Nw_0^i=\frac{1}{N}
  2. 在每一步中，对每一个粒子 xk−1ix_{k-1}^i ，根据状态转移函数产生新的粒子为 xki∼p(xk∣xk−1i)=fk(xk−1i,vk−1i)x_k^i\sim p(x_k|x_{k-1}^i)=f_k(x_{k-1}^i,v_{k-1}^i)
  3. 根据观测值计算重要性权值 wki=wk−1ip(yk∣xki)w_k^i=w_{k-1}^ip(y_k|x_k^i)
  4. 归一化重要性权值 w‾ki=wki∑j=1Nwkj\overline{w}_k^i=\frac{w_k^i}{\sum_{j=1}^Nw_k^j}
  5. 为了避免粒子权重退化而采用重采样，例如当有效粒子数 Neff=1∑iN(wki)2N_{eff}=\frac{1}{\sum_i^N(w_k^i)^2} 低于某个阈值时，按照权重使用重采样方法对粒子进行重采样
  6. 得到 k 时刻的估计值 x^k=∑i=1Nxkiw‾ki\hat{x}_k=\sum_{i=1}^Nx_k^i\overline{w}_k^i

重采样

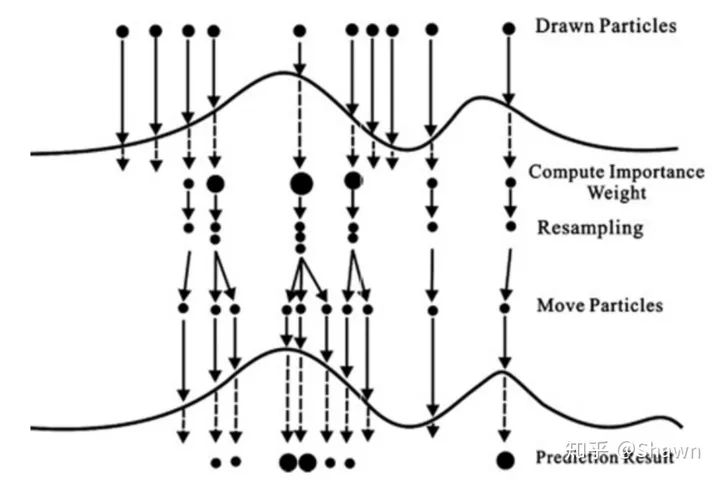
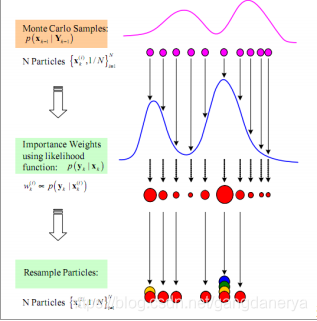
重采样机制是指对于权重较大的粒子序列进行复制，对于权重较小的粒子序列进行抛弃，通过重采样后，我们获得N个权重相等的粒子序列。通过重采样，我们可以避免之前重要性采样中由于权重迭代次数过多导致部分粒子权重很小，部分粒子权重很大的问题。重采样方法主要有系统重采样、残差重采样、多项式重采样等。为了减少计算量我们同时还引入了自适应重采样机制

v2-35c8e9d9f26bbfe26fd11edf60e7ac54_720w.webp

20200324170000786.png

  • 系统重采样，将 (0,1)(0,1) 区间均匀分为 N 份，并将所有粒子按照权重依次进行累加，对于累加后跨过 n 个区间分界点的粒子复制 n 份，对于跨国 0 个区间分类点的粒子抛弃，步骤如下

    1. 在均匀分布 U(0,1/N)U(0,1/N) 中采样 U0U_0
    2. 按照公式 Ui=U0+i−1NU_i=U_0+\frac{i-1}{N} 计算 N 个分界点
    3. 计算每个粒子采样次数 Ni=∑k=1i−1wk≤Ui≤∑k=1iwkN_i=\sum_{k=1}^{i-1}w_k\leq U_i\leq \sum_{k=1}^iw_k

  • 多项式重采样

    另一种常用的方法是多项式重采样，多项式重采样算法首先利用重采样之前的粒子权值集合组成一个多项式分布即 Mult(N;wk(1),wk(2),…,wk(N))Mult(N;w_k(1),w_k(2),…,w_k(N))，并从该多项式分布中抽样 N 次得到 N 个序号（其中每个序号取值为 0-N 之间的整数），然后，对应序号的粒子复制到一个新粒子集合中，该新粒子集合就是重采样后得到的粒子集合

  • 残差重采样

    1. 为每个粒子保留 Ni=⌊Nwki⌋N_i=\lfloor Nw_k^i\rfloor （向下取整）个副本
    2. 剩下的 R=N−∑NiR=N-\sum N_i 从原先的粒子集合中通过随机采样补充，定义每个粒子被随机抽中的概率为 aki=Nwki−NiRa_k^i=\frac{Nw_k^i-N_i}{R}
    3. 最后根据每个粒子数量占比来确定新的权重

重采样步骤

  • t = 0 时刻
    • 初始化得到 N 个粒子 x0x_0
    • 计算 x0x_0 对应的权重 w(x0)w(x_0)
    • 根据权重进行重采样
    • 获取 N 个权重相等的粒子
  • t > 0 时刻
    • 从提议分布 q(xt∣x1:t−1)q(x_t|x_{1:t-1}) 中进行采样
    • 计算 xtx_t 对应的权重 w(xt)w(x_t)
    • 根据就权重进行重采样
    • 获取 N 个权重相等的粒子

SIR 滤波器

SIR 滤波器是粒子滤波器的一种经典实现方式，全称为采样重要性重采样滤波器，通过重要性采样和系统性重采样来近似后验概率分布，适用于非线性、非高斯的状态估计问题

步骤

SIR 滤波器是粒子滤波器的简化，主要步骤包括

  1. 初始化，从先验分布 p(x0)p(x_0) 生成 NN 个粒子 x0i∼p(x0)x_0^i\sim p(x_0) 更新初始化权重 w0i=1Nw_0^i=\frac{1}{N}
  2. 预测，根据状态转移模型 p(xk∣xk−1i)p(x_k|x_{k-1}^i) 生成新粒子 xki∼p(xk∣xk−1i)x_k^i\sim p(x_k|x_{k-1}^i)
  3. 根据观测值计算重要性权值 wki=wk−1ip(yk∣xki)w_k^i=w_{k-1}^ip(y_k|x_k^i)
  4. 归一化重要性权值 w‾ki=wki∑j=1Nwkj\overline{w}_k^i=\frac{w_k^i}{\sum_{j=1}^Nw_k^j}
  5. 不计算 NeffN_{eff} ，直接按照权重进行重新采样，得到新的粒子集合 xkix_{k}^i
  6. 得到 k 时刻的估计值 x^k=∑i=1Nxkiw‾ki\hat{x}_k=\sum_{i=1}^Nx_k^i\overline{w}_k^i

Rao-Blackwellized PF

一种混合的滤波技术，通过结合粒子滤波和解析积分来提高状态估计的效率，利用 Rao-Blackwellization 定理，将状态空间分解为可解析的部分和需要采样的部分，从而减少所需要的粒子数量

Rao-Blockwellization 定理

是一种方差缩减技术，将随机变量 XX 分解为

p(X)=p(X1)p(X2∣X1)p(X)=p(X_1)p(X_2|X_1)

如果 p(X2∣X1)p(X_2|X_1) 可以解析计算，则只需要对 X1X_1 进行采样即可

步骤

  1. 假设状态空间方程可以分解为

    xks=fs(xk−1s,wks)xka=Akxk−1a+Bkxks+wkayk=h(xks,xka,vk)x_k^s=f^s(x_{k-1}^s,w_k^s)\\ x_k^a=A_kx_{k-1}^a+B_kx_k^s+w_k^a\\ y_k=h(x_k^s,x_k^a,v_k)

  2. 采样新状态，从提议分布 q(xks∣xk−1s,i,yk)q(x_k^s|x_{k-1}^{s,i},y_{k}) 中生成新粒子 xks,ix_k^{s,i}

  3. 解析部分预测 xka,ix_k^{a,i} ，这里可以使用卡尔曼滤波得到

  4. 根据观测值 yky_k 计算权重 wki=wk−1ip(yk∣xks,i,xka,i)p(xks,i∣xk−1s,i)q(xks,i∣xk−1s,i,yk)w_k^i=w_{k-1}^i\frac{p(y_k|x_k^{s,i},x_k^{a,i})p(x_k^{s,i}|x_{k-1}^{s,i})}{q(x_k^{s,i}|x_{k-1}^{s,i},y_k)}

  5. 归一化重要性权值 w‾ki=wki∑j=1Nwkj\overline{w}_k^i=\frac{w_k^i}{\sum_{j=1}^Nw_k^j}

  6. 为了避免粒子权重退化而采用重采样，例如当有效粒子数 Neff=1∑iN(wki)2N_{eff}=\frac{1}{\sum_i^N(w_k^i)^2} 低于某个阈值时，按照权重使用重采样方法对粒子进行重采样

  7. 得到 k 时刻的估计值 x^k=∑i=1Nxkiw‾ki\hat{x}_k=\sum_{i=1}^Nx_k^i\overline{w}_k^i

正则化粒子滤波器

是标准粒子滤波器的一种改进，只是在重采样步骤中引入了连续近似，用连续概率密度函数代替离散的粒子集，从而保持粒子多样性

改进的重采样步骤

  1. 构建连续近似分布 p^(xk∣yk)≈∑iNwkiKh(xk−xki)\hat{p}(x_k|y_k)\approx\sum_i^Nw_k^iK_h(x_k-x_k^i) ，其中 Kh(⋅)=1hK(⋅h)K_h(\cdot)=\frac{1}{h}K(\frac{\cdot}{h}) 是缩放核函数，其中 hh 为带宽
  2. 重采样时，根据平滑的分布函数进行采样，从而避免直接幅值高权重粒子，保持粒子多样性

APF 辅助粒子滤波器

辅助粒子滤波器于使用两次加权操作，使产生的粒子权值比通过 SIR 滤波产生的粒子权值变化更稳定，因而得到的估计结果更准确

步骤

  1. 计算每个粒子的前瞻指标，通过 uki=E[Xk∣xk−1i]u_k^i=E[X_k|x_{k-1}^i] 或者 uki∼p(xk∣xk−1i)u_k^i\sim p(x_k|x_{k-1}^i) 计算
  2. 根据先验条件概率抽样新粒子 xki∼p(xk∣xk−1i)x_k^i\sim p(x_k|x_{k-1}^i)
  3. 计算权重 wki=p(yk∣xki)p(zk∣uki)w_k^i=\frac{p(y_k|x_k^i)}{p(z_k|u_k^i)}
  4. 权重归一化 w‾ki=wki∑j=1Nwkj\overline{w}_k^i=\frac{w_k^i}{\sum_{j=1}^Nw_k^j}
  5. 为了避免粒子权重退化而采用重采样，例如当有效粒子数 Neff=1∑iN(wki)2N_{eff}=\frac{1}{\sum_i^N(w_k^i)^2} 低于某个阈值时，按照权重使用重采样方法对粒子进行重采样
  6. 得到 k 时刻的估计值 x^k=∑i=1Nxkiw‾ki\hat{x}_k=\sum_{i=1}^Nx_k^i\overline{w}_k^i