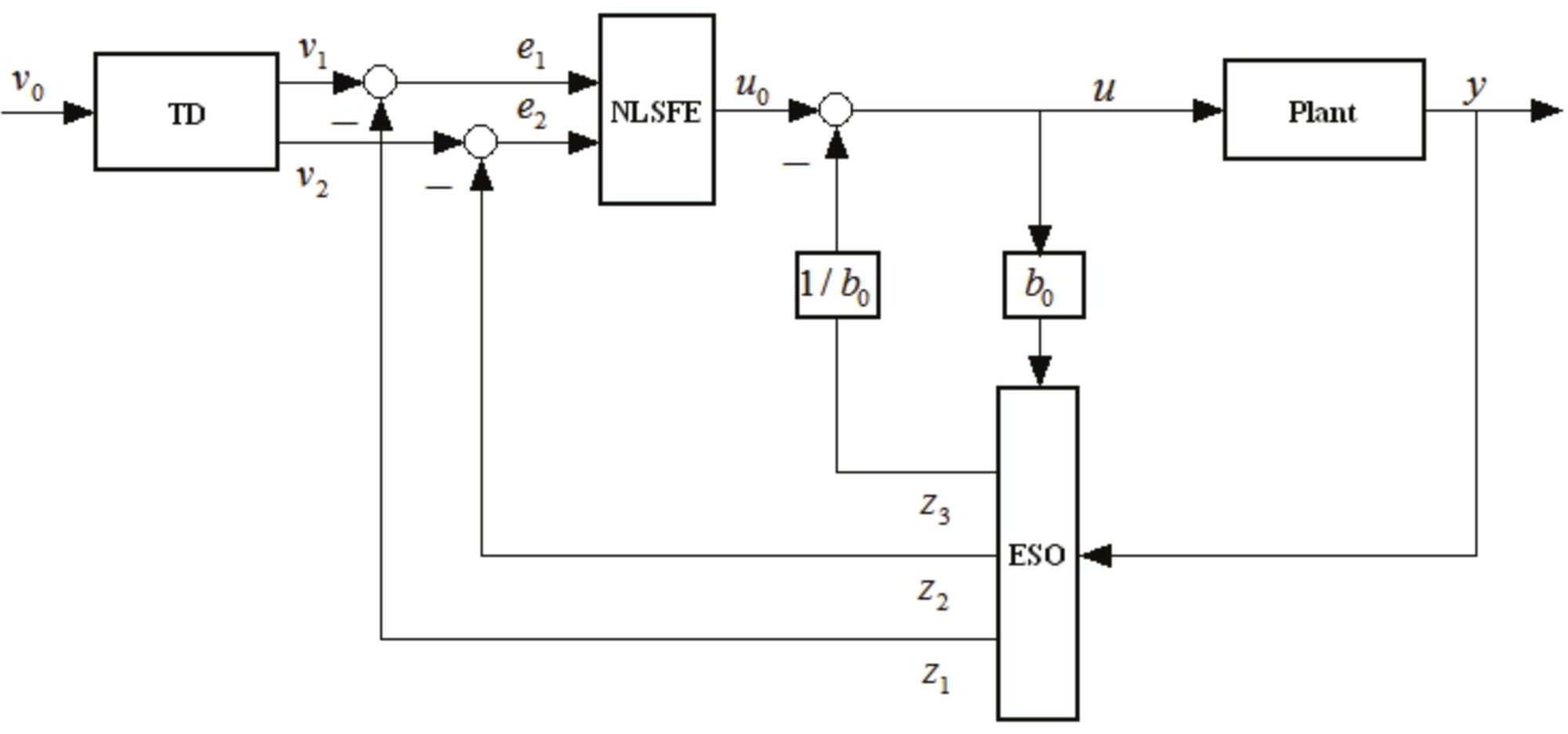
为了解决快速性和超调的矛盾,在控制器设计过程中引入了过渡过程,通俗的讲就是输入信号从初始值到目标值并不是阶跃的,而是平滑过渡的,并且这个过渡过程的时间长短是可以调节的。将过渡过程和微分器在一个模块中实现,称为**跟踪-微分器(TD),**单独的过渡过程和速度规划并没有本质区别。但是TD和速度规划不是一回事,TD将输入过渡和微分器统一为一个模块,它一边尽可能快地跟踪输入信号,同时给出输入信号近似的微分。
自抗扰控制对扰动和不确定性的处理是自抗扰控制最突出的特征,它把作用于被控对象的所有不确定因素都归结为“未知扰动”,而用被控对象的输入输出数据对它进行估计,并给予补偿。“自抗扰”的名称也来源于此,即主动抵抗干扰,不需要直接测量外扰的作用,也不需要实现知道扰动的规律(能知道更好)。构建观测器,利用被控对象的输入、输出和所施加的控制输入来估计作用于系统的总扰动(包括内扰和外扰,可以粗浅地理解为所有的影响因素),实现这一功能的模块被称为扩展状态观测器 (Extended State Observer,ESO)。这个名字也与观测器的形式十分匹配,因为在设计ESO时,首先构造一个扩张的系统,此系统的阶数比被控对象的阶数高一阶,ESO就是估计扩张系统的状态。观测出系统的总扰动,在设计控制器时首先抵消掉这个扰动,将得到一个标准的串联积分型系统,基于此标准型系统设计控制器时,控制器的形式与PID的形式类型,一般利用误差和误差的微分来构造控制器,这里的误差及其微分是由TD的输出和ESO的输出构造的。韩老师在其专著中给出了常用的几种非线性状态误差反馈控制律 (Nonlinear State Error Feedback,NLSEF)。
被控对象可以有时延,可以有右半平面的零点或极点,但不能在右半平面同时有零点和极点。同时有右半平面的零点和极点,意味着有根轨迹从右半平面出发有回到右半平面,可能一直在右半平面,这样控制器设计是十分困难的。
被控对象的型次要求:对象不含微分器,且型次要求允许控制器含一个积分器。LADRC本身含一个积分器,如果被控对象含微分器,会出现原点的零极点对消。允许控制器含一个积分器是因为LADRC中是一定含有一个积分器的。
LTD
是由一阶低通滤波器 r s + r \frac{r}{s + r} s + r r r r r r r r v v v
令
X = [ x 1 ] x 1 = y X=\begin{bmatrix}x_1\end{bmatrix}\\x_1=y
X = [ x 1 ] x 1 = y
从上式的低通滤波的传递函数可以推导出系统的状态方程
X ˙ = A X + B u = [ − r ] X + [ r ] u Y = [ 1 ] X + [ 0 ] u \dot{X}=AX+Bu=\begin{bmatrix}-r\end{bmatrix}X+[r]u\\Y=[1]X+[0]u
X ˙ = A X + B u = [ − r ] X + [ r ] u Y = [ 1 ] X + [ 0 ] u
输出,这里的 u 表示输入的期望值,LTD 是对期望值进行处理的
x 1 ( k + 1 ) = h x 1 ˙ ( k ) + x 1 ( k ) = h ( − r x 1 ( k ) + r u ) + x 1 ( k ) x_1(k+1)=h\dot{x_1}(k)+x_1(k) =h(-rx_1(k) + ru)+x_1(k)
x 1 ( k + 1 ) = h x 1 ˙ ( k ) + x 1 ( k ) = h ( − r x 1 ( k ) + r u ) + x 1 ( k )
LESO
从上述LTD中可知,这一步实际上是把扰动合并,将输入输出噪声与模型上的误差合并,从而得到下列式子。其中 f f f
y ′ = f ( x 1 ) + b u = f ( x 1 ) + b 0 u − b 0 u + b u = f + b 0 u y'=f(x_1)+bu= f(x_1) + b_0u - b_0u + bu=f+b_0u
y ′ = f ( x 1 ) + b u = f ( x 1 ) + b 0 u − b 0 u + b u = f + b 0 u
在一阶的 ADRC 中,LESO 是二阶的,具体形式为
令
Z = [ z 1 z 2 ] Z=\begin{bmatrix}z_1\\z_2\end{bmatrix}
Z = [ z 1 z 2 ]
并且
z 1 → x 1 = y z 2 → f 扰动 z_1\rightarrow x_1=y\\z_2\rightarrow f~扰动
z 1 → x 1 = y z 2 → f 扰 动
得
Z ˙ = A Z + B u + L ( x 1 − z 1 ) y ^ = C Z \dot{Z}=AZ+Bu+L(x_1-z_1)\\\hat{y}=CZ
Z ˙ = A Z + B u + L ( x 1 − z 1 ) y ^ = C Z
其中
L = [ β 1 β 2 β 3 ] L=\begin{bmatrix}\beta_1\\\beta_2\\\beta_3\end{bmatrix}
L = ⎣ ⎢ ⎡ β 1 β 2 β 3 ⎦ ⎥ ⎤
带入
{ [ z 1 ˙ z 2 ˙ ] = [ − β 1 1 − β 2 0 ] [ z 1 z 2 ] + [ b 0 β 1 0 β 2 ] [ u y ] y ^ = [ 1 0 0 1 ] [ z 1 z 2 ] \left\{\begin{aligned}\left.\begin{bmatrix}\dot{z_1}\\\dot{z_2}\end{bmatrix}\right.&=&\left.\begin{bmatrix}-\beta_1&1\\-\beta_2&0\end{bmatrix}\right.\left.\begin{bmatrix}z_1\\z_2\end{bmatrix}\right.+\left.\begin{bmatrix}b_0&\beta_1\\0&\beta_2\end{bmatrix}\right.\left.\begin{bmatrix}u\\y\end{bmatrix}\right.\\\hat{y}&=&\left.\begin{bmatrix}1&0\\0&1\end{bmatrix}\right.\left.\begin{bmatrix}z_1\\z_2\end{bmatrix}\right.\end{aligned}\right.
⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ [ z 1 ˙ z 2 ˙ ] y ^ = = [ − β 1 − β 2 1 0 ] [ z 1 z 2 ] + [ b 0 0 β 1 β 2 ] [ u y ] [ 1 0 0 1 ] [ z 1 z 2 ]
其中 β \beta β
L E S O ( s ) = s n + 1 + β 1 s n + β 2 s n − 1 + … + β n − 1 L_{ESO}(s)=s^{n+1}+\beta_1 s^n + \beta_2 s^{n-1}+…+\beta_{n-1}
L E S O ( s ) = s n + 1 + β 1 s n + β 2 s n − 1 + … + β n − 1
将极点都配置到左半轴同一位置,可以将调节参数缩减为
L E S O ( s ) = ( s + w o ) n + 1 = 0 L_{ESO}(s)=(s+w_o)^{n+1}=0
L E S O ( s ) = ( s + w o ) n + 1 = 0
其中 w o w_o w o β \beta β
输入为 u , y u, y u , y
输出为
z 1 ( k + 1 ) = z 1 ( k ) + h z 1 ˙ ( k ) = z 1 ( k ) + h ( − β 1 z 1 ( k ) + z 2 ( k ) + b 0 u + β 1 y ) z 2 ( k + 1 ) = z 2 ( k ) + h z 2 ˙ ( k ) = z 2 ( k ) + h ( − β 2 z 1 ( k ) + β 2 y ) z_1(k+1)=z_1(k)+h\dot{z_1}(k)=z_1(k)+h(-\beta_1z_1(k)+z_2(k)+b_0u+\beta_1y)\\z_2(k+1)=z_2(k)+h\dot{z_2}(k)=z_2(k)+h(-\beta_2z_1(k)+\beta_2y)
z 1 ( k + 1 ) = z 1 ( k ) + h z 1 ˙ ( k ) = z 1 ( k ) + h ( − β 1 z 1 ( k ) + z 2 ( k ) + b 0 u + β 1 y ) z 2 ( k + 1 ) = z 2 ( k ) + h z 2 ˙ ( k ) = z 2 ( k ) + h ( − β 2 z 1 ( k ) + β 2 y )
LSEF
令
e 1 = x 1 − z 1 u 0 = a 1 × e 1 u = u 0 − z 2 b 0 e_1 = x_1 - z_1\\u_0 = a_1 \times e_1\\u=\frac{u_0-z_2}{b_0}
e 1 = x 1 − z 1 u 0 = a 1 × e 1 u = b 0 u 0 − z 2
其中 a 1 a_1 a 1
L S E F ( s ) = s n + a n s n − 1 + … + a 2 s + a 1 L_{SEF}(s)=s^n+a_ns^{n-1}+…+a_2s+a_1
L S E F ( s ) = s n + a n s n − 1 + … + a 2 s + a 1
将特征值统一配置在左半实轴同一位置,得到
L S E F ( s ) = ( s + w c ) n L_{SEF}(s)=(s+w_c)^{n}
L S E F ( s ) = ( s + w c ) n
其中 w c w_c w c
LTD
二阶LTD是由二阶低通滤波器传递函数 r 2 s 2 + 2 r s + r 2 \frac{r^2}{s^2+2rs+r^2} s 2 + 2 r s + r 2 r 2 r r r r r r v v v
令
X = [ x 1 x 2 ] { x 1 = y x 2 = x 1 ˙ X=\begin{bmatrix}x_1\\x_2\end{bmatrix}\\
\left\{\begin{aligned}x_1 = y\\x_2=\dot{x_1}\end{aligned}\right.
X = [ x 1 x 2 ] { x 1 = y x 2 = x 1 ˙
从上式的低通滤波的传递函数可以推导出系统的状态方程
X ˙ = A X + B u = [ 0 1 − r 2 − 2 r ] X + [ 0 r 2 ] u Y = [ 1 0 ] X + [ 0 ] u \dot{X}=AX+Bu=\begin{bmatrix}0&1\\-r^2&-2r\end{bmatrix}X+\begin{bmatrix}0\\r^2\end{bmatrix}u\\Y=\begin{bmatrix}1\\0\end{bmatrix}X+[0]u
X ˙ = A X + B u = [ 0 − r 2 1 − 2 r ] X + [ 0 r 2 ] u Y = [ 1 0 ] X + [ 0 ] u
输出,这里的 u 表示输入的期望值,LTD 是对期望值进行处理的
x 1 ( k + 1 ) = h x 2 ( k ) + x 1 ( k ) x 2 ( k + 1 ) = h ( − r 2 x 1 ( k ) − 2 r x 2 ( k ) + r 2 u ) + x 2 ( k ) x_1(k+1)=hx_2(k)+x_1(k)\\x_2(k+1) =h(-r^2 x_1(k) - 2rx_2(k)+r^2 u)+x_2(k)
x 1 ( k + 1 ) = h x 2 ( k ) + x 1 ( k ) x 2 ( k + 1 ) = h ( − r 2 x 1 ( k ) − 2 r x 2 ( k ) + r 2 u ) + x 2 ( k )
LESO
从上述LTD中可知,这一步实际上是把扰动合并,将输入输出噪声与模型上的误差合并,从而得到下列式子。其中 f f f
y ′ ′ = f ( x 1 ) + b u = f ( x 1 ) + b 0 u − b 0 u + b u = f + b 0 u y''=f(x_1)+bu= f(x_1) + b_0u - b_0u + bu=f+b_0u
y ′ ′ = f ( x 1 ) + b u = f ( x 1 ) + b 0 u − b 0 u + b u = f + b 0 u
在一阶的 ADRC 中,LESO 是二阶的,具体形式为
令
Z = [ z 1 z 2 z 3 ] Z=\begin{bmatrix}z_1\\z_2\\z_3\end{bmatrix}
Z = ⎣ ⎢ ⎡ z 1 z 2 z 3 ⎦ ⎥ ⎤
并且
z 1 → x 1 = y z 2 → x 2 = y ˙ z 3 → f 扰动 z_1\rightarrow x_1=y\\z_2\rightarrow x_2=\dot{y}\\z_3\rightarrow f~扰动
z 1 → x 1 = y z 2 → x 2 = y ˙ z 3 → f 扰 动
得
Z ˙ = A Z + B u + L ( x 1 − z 1 ) y ^ = C Z \dot{Z}=AZ+Bu+L(x_1-z_1)\\\hat{y}=CZ
Z ˙ = A Z + B u + L ( x 1 − z 1 ) y ^ = C Z
其中
L = [ β 1 β 2 β 3 ] L=\begin{bmatrix}\beta_1\\\beta_2\\\beta_3\end{bmatrix}
L = ⎣ ⎢ ⎡ β 1 β 2 β 3 ⎦ ⎥ ⎤
带入得
{ [ z 1 ˙ z 2 ˙ z 3 ˙ ] = [ − β 1 1 0 − β 2 0 1 − β 3 0 0 ] [ z 1 z 2 z 3 ] + [ 0 β 1 b 0 β 2 0 β 3 ] [ u y ] y ^ = [ 1 0 0 0 1 0 0 0 1 ] [ z 1 z 2 z 3 ] \left\{\begin{aligned}\left.\begin{bmatrix}\dot{z_1}\\\dot{z_2}\\\dot{z_3}\end{bmatrix}\right.&=&\left.\begin{bmatrix}-\beta_1&1&0\\-\beta_2&0&1\\-\beta_3&0&0\end{bmatrix}\right.\left.\begin{bmatrix}z_1\\z_2\\z_3\end{bmatrix}\right.+\left.\begin{bmatrix}0&\beta_1\\b_0&\beta_2\\0&\beta_3\end{bmatrix}\right.\left.\begin{bmatrix}u\\y\end{bmatrix}\right.\\\hat{y}&=&\left.\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}\right.\left.\begin{bmatrix}z_1\\z_2\\z_3\end{bmatrix}\right.\end{aligned}\right.
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ ⎣ ⎢ ⎡ z 1 ˙ z 2 ˙ z 3 ˙ ⎦ ⎥ ⎤ y ^ = = ⎣ ⎢ ⎡ − β 1 − β 2 − β 3 1 0 0 0 1 0 ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ z 1 z 2 z 3 ⎦ ⎥ ⎤ + ⎣ ⎢ ⎡ 0 b 0 0 β 1 β 2 β 3 ⎦ ⎥ ⎤ [ u y ] ⎣ ⎢ ⎡ 1 0 0 0 1 0 0 0 1 ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ z 1 z 2 z 3 ⎦ ⎥ ⎤
其中 β \beta β
L E S O ( s ) = s n + 1 + β 1 s n + β 2 s n − 1 + … + β n − 1 L_{ESO}(s)=s^{n+1}+\beta_1 s^n + \beta_2 s^{n-1}+…+\beta_{n-1}
L E S O ( s ) = s n + 1 + β 1 s n + β 2 s n − 1 + … + β n − 1
将极点都配置到左半轴同一位置,可以将调节参数缩减为
L E S O ( s ) = ( s + w o ) n + 1 = 0 L_{ESO}(s)=(s+w_o)^{n+1}=0
L E S O ( s ) = ( s + w o ) n + 1 = 0
其中 w o w_o w o β \beta β
输入为 u , y u, y u , y
输出为
z 1 ( k + 1 ) = z 1 ( k ) + h z 1 ˙ ( k ) = z 1 ( k ) + h ( − β 1 z 1 ( k ) + z 2 ( k ) + β 1 y ) z 2 ( k + 1 ) = z 2 ( k ) + h z 2 ˙ ( k ) = z 2 ( k ) + h ( − β 2 z 1 ( k ) + z 3 ( k ) + b 0 u + β 2 y ) z 3 ( k + 1 ) = z 3 ( k ) + h z 3 ˙ ( k ) = z 3 ( k ) + h ( − β 3 z 1 ( k ) + β 3 y ) z_1(k+1)=z_1(k)+h\dot{z_1}(k)=z_1(k)+h(-\beta_1z_1(k)+z_2(k)+\beta_1y)\\z_2(k+1)=z_2(k)+h\dot{z_2}(k)=z_2(k)+h(-\beta_2z_1(k)+z_3(k)+b_0u+\beta_2y)\\z_3(k+1)=z_3(k)+h\dot{z_3}(k)=z_3(k)+h(-\beta_3z_1(k)+\beta_3y)
z 1 ( k + 1 ) = z 1 ( k ) + h z 1 ˙ ( k ) = z 1 ( k ) + h ( − β 1 z 1 ( k ) + z 2 ( k ) + β 1 y ) z 2 ( k + 1 ) = z 2 ( k ) + h z 2 ˙ ( k ) = z 2 ( k ) + h ( − β 2 z 1 ( k ) + z 3 ( k ) + b 0 u + β 2 y ) z 3 ( k + 1 ) = z 3 ( k ) + h z 3 ˙ ( k ) = z 3 ( k ) + h ( − β 3 z 1 ( k ) + β 3 y )
LSEF
令
e 1 = x 1 − z 1 e 2 = x 2 − z 2 u 0 = a 1 e 1 + a 2 e 2 u = u 0 − z 3 b 0 e_1 = x_1 - z_1\\e_2=x_2-z_2\\u_0 = a_1 e_1+a_2e_2\\u=\frac{u_0-z_3}{b_0}
e 1 = x 1 − z 1 e 2 = x 2 − z 2 u 0 = a 1 e 1 + a 2 e 2 u = b 0 u 0 − z 3
其中 a 1 a_1 a 1
L S E F ( s ) = s n + a n s n − 1 + … + a 2 s + a 1 L_{SEF}(s)=s^n+a_ns^{n-1}+…+a_2s+a_1
L S E F ( s ) = s n + a n s n − 1 + … + a 2 s + a 1
将特征值统一配置在左半实轴同一位置,得到
L S E F ( s ) = ( s + w c ) n L_{SEF}(s)=(s+w_c)^{n}
L S E F ( s ) = ( s + w c ) n
其中 w c w_c w c
LTD
三阶 LTD 是由三阶低通滤波传递函数 r 3 s 3 + 3 r s 2 + 3 r 2 s + r 3 \frac{r^3}{s^3+3rs^2+3r^2s+r^3} s 3 + 3 r s 2 + 3 r 2 s + r 3 r 3
令
X = [ x 1 x 2 x 3 ] { x 1 = y x 2 = x 1 ˙ x 3 = x 2 ˙ X=\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}\\\left\{\begin{aligned}x_1 = y\\x_2=\dot{x_1}\\x_3=\dot{x_2} \end{aligned}\right.
X = ⎣ ⎢ ⎡ x 1 x 2 x 3 ⎦ ⎥ ⎤ ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ x 1 = y x 2 = x 1 ˙ x 3 = x 2 ˙
得
X ˙ = [ 0 1 0 0 0 1 − r 3 − 3 r 2 − 3 r ] X + [ 0 0 r 3 ] u y = [ 1 0 0 ] X + [ 0 ] u \dot{X}=\begin{bmatrix}0&1&0\\0&0&1\\-r^3&-3r^2&-3r\end{bmatrix}X+\begin{bmatrix}0\\0\\r^3\end{bmatrix}u\\y=\begin{bmatrix}1\\0\\0\end{bmatrix}X+\begin{bmatrix}0\end{bmatrix}u
X ˙ = ⎣ ⎢ ⎡ 0 0 − r 3 1 0 − 3 r 2 0 1 − 3 r ⎦ ⎥ ⎤ X + ⎣ ⎢ ⎡ 0 0 r 3 ⎦ ⎥ ⎤ u y = ⎣ ⎢ ⎡ 1 0 0 ⎦ ⎥ ⎤ X + [ 0 ] u
输出,这里的 u 表示输入的期望值,LTD 是对期望值进行处理的
x 1 ( k + 1 ) = h x 2 ( k ) + x 1 ( k ) x 2 ( k + 1 ) = h x 3 ( k ) + x 2 ( k ) x 3 ( k + 1 ) = h ( − r 3 x 1 ( k ) − 3 r 2 x 2 ( k ) − 3 r x 3 ( k ) + r 3 u ) + x 3 ( k ) x_1(k+1)=hx_2(k)+x_1(k)\\x_2(k+1) =hx_3(k)+x_2(k)\\x_3(k+1) =h(-r^3 x_1(k) - 3r^2x_2(k) -3rx_3(k)+r^3 u)+x_3(k)
x 1 ( k + 1 ) = h x 2 ( k ) + x 1 ( k ) x 2 ( k + 1 ) = h x 3 ( k ) + x 2 ( k ) x 3 ( k + 1 ) = h ( − r 3 x 1 ( k ) − 3 r 2 x 2 ( k ) − 3 r x 3 ( k ) + r 3 u ) + x 3 ( k )
LESO
由上式可以得出
y ′ ′ ′ = f ( x 1 , x 2 , x 3 ) + b u = f + b 0 u y^{'''}=f(x_1, x_2, x_3) + bu\\=f+b_0u
y ′ ′ ′ = f ( x 1 , x 2 , x 3 ) + b u = f + b 0 u
此时引入 z z z
{ z 1 → x 1 z 2 → x 2 z 3 → x 3 z 4 → f Z = [ z 1 z 2 z 3 z 4 ] \left\{\begin{aligned}z_1\rightarrow x_1\\z_2\rightarrow x_2\\z_3\rightarrow x_3\\z_4\rightarrow f\end{aligned}\right.\\Z=\begin{bmatrix}z_1\\z_2\\z_3\\z_4\end{bmatrix}
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ z 1 → x 1 z 2 → x 2 z 3 → x 3 z 4 → f Z = ⎣ ⎢ ⎢ ⎢ ⎡ z 1 z 2 z 3 z 4 ⎦ ⎥ ⎥ ⎥ ⎤
可得
Z ˙ = [ 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 ] Z + [ 0 0 b 0 0 ] u + L ( x 1 − z 1 ) y ^ = C Z + D u \dot{Z}=\begin{bmatrix}0&1&0&0\\0&0&1&0\\0&0&0&1\\0&0&0&0\end{bmatrix}Z+\begin{bmatrix}0\\0\\b_0\\0\end{bmatrix}u+L(x_1-z_1)\\\hat{y}=CZ+Du
Z ˙ = ⎣ ⎢ ⎢ ⎢ ⎡ 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 ⎦ ⎥ ⎥ ⎥ ⎤ Z + ⎣ ⎢ ⎢ ⎢ ⎡ 0 0 b 0 0 ⎦ ⎥ ⎥ ⎥ ⎤ u + L ( x 1 − z 1 ) y ^ = C Z + D u
其中
L = [ β 1 β 2 β 3 β 4 ] L=\begin{bmatrix}\beta_1\\\beta_2\\\beta_3\\\beta_4\end{bmatrix}
L = ⎣ ⎢ ⎢ ⎢ ⎡ β 1 β 2 β 3 β 4 ⎦ ⎥ ⎥ ⎥ ⎤
带入得
Z ˙ = [ − β 1 1 0 0 − β 2 0 1 0 − β 3 0 0 1 − β 4 0 0 0 ] Z + [ 0 β 1 0 β 2 b 0 β 3 0 β 4 ] [ u y ] y ^ = C Z + D u = [ 1 0 0 0 ] [ z 1 z 2 z 3 z 4 ] \dot{Z}=\begin{bmatrix}-\beta_1&1&0&0\\-\beta_2&0&1&0\\-\beta_3&0&0&1\\-\beta_4&0&0&0\end{bmatrix}Z+\begin{bmatrix}0&\beta_1\\0&\beta_2\\b_0&\beta_3\\0&\beta_4\end{bmatrix}\begin{bmatrix}u\\y\end{bmatrix}\\\hat{y}=CZ+Du=\begin{bmatrix}1&0&0&0\end{bmatrix}\begin{bmatrix}z_1\\z_2\\z_3\\z_4\end{bmatrix}
Z ˙ = ⎣ ⎢ ⎢ ⎢ ⎡ − β 1 − β 2 − β 3 − β 4 1 0 0 0 0 1 0 0 0 0 1 0 ⎦ ⎥ ⎥ ⎥ ⎤ Z + ⎣ ⎢ ⎢ ⎢ ⎡ 0 0 b 0 0 β 1 β 2 β 3 β 4 ⎦ ⎥ ⎥ ⎥ ⎤ [ u y ] y ^ = C Z + D u = [ 1 0 0 0 ] ⎣ ⎢ ⎢ ⎢ ⎡ z 1 z 2 z 3 z 4 ⎦ ⎥ ⎥ ⎥ ⎤
其中 β \beta β
L E S O ( s ) = s n + 1 + β 1 s n + β 2 s n − 1 + … + β n − 1 L_{ESO}(s)=s^{n+1}+\beta_1 s^n + \beta_2 s^{n-1}+…+\beta_{n-1}
L E S O ( s ) = s n + 1 + β 1 s n + β 2 s n − 1 + … + β n − 1
将极点都配置到左半轴同一位置,可以将调节参数缩减为
L E S O ( s ) = ( s + w o ) n + 1 = 0 L_{ESO}(s)=(s+w_o)^{n+1}=0
L E S O ( s ) = ( s + w o ) n + 1 = 0
其中 w o w_o w o β \beta β
输入为 u , y u, y u , y
输出为
z 1 ( k + 1 ) = z 1 ( k ) + h z 1 ˙ ( k ) = z 1 ( k ) + h ( − β 1 z 1 ( k ) + z 2 ( k ) + β 1 y ) z 2 ( k + 1 ) = z 2 ( k ) + h z 2 ˙ ( k ) = z 2 ( k ) + h ( − β 2 z 1 ( k ) + z 3 ( k ) + β 2 y ) z 3 ( k + 1 ) = z 3 ( k ) + h z 3 ˙ ( k ) = z 3 ( k ) + h ( − β 3 z 1 ( k ) + z 4 ( k ) + b 0 u + β 3 y ) z 4 ( k + 1 ) = z 4 ( k ) + h z 4 ˙ ( k ) = z 4 ( k ) + h ( − β 4 z 1 ( k ) + β 4 y ) z_1(k+1)=z_1(k)+h\dot{z_1}(k)=z_1(k)+h(-\beta_1z_1(k)+z_2(k)+\beta_1y)\\z_2(k+1)=z_2(k)+h\dot{z_2}(k)=z_2(k)+h(-\beta_2z_1(k)+z_3(k)+\beta_2y)\\z_3(k+1)=z_3(k)+h\dot{z_3}(k)=z_3(k)+h(-\beta_3z_1(k)+z_4(k)+b_0u+\beta_3y)\\z_4(k+1)=z_4(k)+h\dot{z_4}(k)=z_4(k)+h(-\beta_4z_1(k)+\beta_4y)
z 1 ( k + 1 ) = z 1 ( k ) + h z 1 ˙ ( k ) = z 1 ( k ) + h ( − β 1 z 1 ( k ) + z 2 ( k ) + β 1 y ) z 2 ( k + 1 ) = z 2 ( k ) + h z 2 ˙ ( k ) = z 2 ( k ) + h ( − β 2 z 1 ( k ) + z 3 ( k ) + β 2 y ) z 3 ( k + 1 ) = z 3 ( k ) + h z 3 ˙ ( k ) = z 3 ( k ) + h ( − β 3 z 1 ( k ) + z 4 ( k ) + b 0 u + β 3 y ) z 4 ( k + 1 ) = z 4 ( k ) + h z 4 ˙ ( k ) = z 4 ( k ) + h ( − β 4 z 1 ( k ) + β 4 y )
LSEF
令
e 1 = x 1 − z 1 e 2 = x 2 − z 2 e 3 = x 3 − z 3 u 0 = a 1 e 1 + a 2 e 2 + a 3 e 3 u = u 0 − z 4 b 0 e_1 = x_1 - z_1\\e_2=x_2-z_2\\e_3=x_3-z_3\\u_0 = a_1 e_1+a_2e_2+a_3e_3\\u=\frac{u_0-z_4}{b_0}
e 1 = x 1 − z 1 e 2 = x 2 − z 2 e 3 = x 3 − z 3 u 0 = a 1 e 1 + a 2 e 2 + a 3 e 3 u = b 0 u 0 − z 4
其中 a 1 a_1 a 1
L S E F ( s ) = s n + a n s n − 1 + … + a 2 s + a 1 L_{SEF}(s)=s^n+a_ns^{n-1}+…+a_2s+a_1
L S E F ( s ) = s n + a n s n − 1 + … + a 2 s + a 1
将特征值统一配置在左半实轴同一位置,得到
L S E F ( s ) = ( s + w c ) n L_{SEF}(s)=(s+w_c)^{n}
L S E F ( s ) = ( s + w c ) n
其中 w c w_c w c
LTD
四阶 LTD 是由三阶低通滤波传递函数 r 4 s 4 + 4 r s 3 + 6 r 2 s 2 + 4 r 3 s + r 4 \frac{r^4}{s^4+4rs^3+6r^2s^2+4r^3s+r^4} s 4 + 4 r s 3 + 6 r 2 s 2 + 4 r 3 s + r 4 r 4
令
X = [ x 1 x 2 x 3 x 4 ] { x 1 = y x 2 = x 1 ˙ x 3 = x 2 ˙ x 4 = x 3 ˙ X=\begin{bmatrix}x_1\\x_2\\x_3\\x_4\end{bmatrix}\\\left\{\begin{aligned}x_1 = y\\x_2=\dot{x_1}\\x_3=\dot{x_2}\\x_4 = \dot{x_3}\end{aligned}\right.
X = ⎣ ⎢ ⎢ ⎢ ⎡ x 1 x 2 x 3 x 4 ⎦ ⎥ ⎥ ⎥ ⎤ ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ x 1 = y x 2 = x 1 ˙ x 3 = x 2 ˙ x 4 = x 3 ˙
得
X ˙ = [ 0 1 0 0 0 0 1 0 0 0 0 1 − r 4 − 4 r 3 − 6 r 2 − 4 r ] X + [ 0 0 0 r 4 ] u y = [ 1 0 0 0 ] X + [ 0 ] u \dot{X}=\begin{bmatrix}0&1&0&0\\0&0&1&0\\0&0&0&1\\-r^4&-4r^3&-6r^2&-4r\end{bmatrix}X+\begin{bmatrix}0\\0\\0\\r^4\end{bmatrix}u\\y=\begin{bmatrix}1\\0\\0\\0\end{bmatrix}X+\begin{bmatrix}0\end{bmatrix}u
X ˙ = ⎣ ⎢ ⎢ ⎢ ⎡ 0 0 0 − r 4 1 0 0 − 4 r 3 0 1 0 − 6 r 2 0 0 1 − 4 r ⎦ ⎥ ⎥ ⎥ ⎤ X + ⎣ ⎢ ⎢ ⎢ ⎡ 0 0 0 r 4 ⎦ ⎥ ⎥ ⎥ ⎤ u y = ⎣ ⎢ ⎢ ⎢ ⎡ 1 0 0 0 ⎦ ⎥ ⎥ ⎥ ⎤ X + [ 0 ] u
输出,这里的 u 表示输入的期望值,LTD 是对期望值进行处理的
x 1 ( k + 1 ) = h x 2 ( k ) + x 1 ( k ) x 2 ( k + 1 ) = h x 3 ( k ) + x 2 ( k ) x 3 ( k + 1 ) = h x 4 ( k ) + x 3 ( k ) x 4 ( k + 1 ) = h ( − r 4 x 1 ( k ) − 4 r 3 x 2 ( k ) − 6 r 2 x 3 ( k ) − 4 r x 4 ( k ) + r 4 u ) + x 4 ( k ) x_1(k+1)=hx_2(k)+x_1(k)\\x_2(k+1) =hx_3(k)+x_2(k)\\x_3(k+1) =hx_4(k)+x_3(k)\\x_4(k+1) =h(-r^4 x_1(k) - 4r^3x_2(k) -6r^2x_3(k)-4rx_4(k)+r^4 u)+x_4(k)
x 1 ( k + 1 ) = h x 2 ( k ) + x 1 ( k ) x 2 ( k + 1 ) = h x 3 ( k ) + x 2 ( k ) x 3 ( k + 1 ) = h x 4 ( k ) + x 3 ( k ) x 4 ( k + 1 ) = h ( − r 4 x 1 ( k ) − 4 r 3 x 2 ( k ) − 6 r 2 x 3 ( k ) − 4 r x 4 ( k ) + r 4 u ) + x 4 ( k )
LESO
由上式可以得出
y ′ ′ ′ ′ = f ( x 1 , x 2 , x 3 , x 4 ) + b u = f + b 0 u y^{''''}=f(x_1, x_2, x_3, x_4) + bu\\=f+b_0u
y ′ ′ ′ ′ = f ( x 1 , x 2 , x 3 , x 4 ) + b u = f + b 0 u
此时引入 z z z
{ z 1 → x 1 z 2 → x 2 z 3 → x 3 z 4 → x 4 z 5 → f Z = [ z 1 z 2 z 3 z 4 z 5 ] \left\{\begin{aligned}z_1\rightarrow x_1\\z_2\rightarrow x_2\\z_3\rightarrow x_3\\z_4\rightarrow x_4\\z_5\rightarrow f\end{aligned}\right.\\Z=\begin{bmatrix}z_1\\z_2\\z_3\\z_4\\z_5\end{bmatrix}
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ z 1 → x 1 z 2 → x 2 z 3 → x 3 z 4 → x 4 z 5 → f Z = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ z 1 z 2 z 3 z 4 z 5 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
可得
Z ˙ = [ 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 ] Z + [ 0 0 0 b 0 0 ] u + L ( x 1 − z 1 ) y ^ = C Z + D u \dot{Z}=\begin{bmatrix}0&1&0&0&0\\0&0&1&0&0\\0&0&0&1&0\\0&0&0&0&1\\0&0&0&0&0\end{bmatrix}Z+\begin{bmatrix}0\\0\\0\\b_0\\0\end{bmatrix}u+L(x_1-z_1)\\\hat{y}=CZ+Du
Z ˙ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ Z + ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 0 0 0 b 0 0 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ u + L ( x 1 − z 1 ) y ^ = C Z + D u
其中
L = [ β 1 β 2 β 3 β 4 β 5 ] L=\begin{bmatrix}\beta_1\\\beta_2\\\beta_3\\\beta_4\\\beta_5\end{bmatrix}
L = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ β 1 β 2 β 3 β 4 β 5 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
带入得
Z ˙ = [ − β 1 1 0 0 0 − β 2 0 1 0 0 − β 3 0 0 1 0 − β 4 0 0 0 1 − β 5 0 0 0 0 ] Z + [ 0 β 1 0 β 2 0 β 3 b 0 β 4 0 β 5 ] [ u y ] y ^ = C Z + D u = [ 1 0 0 0 0 ] [ z 1 z 2 z 3 z 4 z 5 ] \dot{Z}=\begin{bmatrix}-\beta_1&1&0&0&0\\-\beta_2&0&1&0&0\\-\beta_3&0&0&1&0\\-\beta_4&0&0&0&1\\-\beta_5&0&0&0&0 \end{bmatrix}Z+\begin{bmatrix}0&\beta_1\\0&\beta_2\\0&\beta_3\\b_0&\beta_4\\0&\beta_5\end{bmatrix}\begin{bmatrix}u\\y\end{bmatrix}\\\hat{y}=CZ+Du=\begin{bmatrix}1&0&0&0&0\end{bmatrix}\begin{bmatrix}z_1\\z_2\\z_3\\z_4\\z_5\end{bmatrix}
Z ˙ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ − β 1 − β 2 − β 3 − β 4 − β 5 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ Z + ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 0 0 0 b 0 0 β 1 β 2 β 3 β 4 β 5 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ [ u y ] y ^ = C Z + D u = [ 1 0 0 0 0 ] ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ z 1 z 2 z 3 z 4 z 5 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
其中 β \beta β
L E S O ( s ) = s n + 1 + β 1 s n + β 2 s n − 1 + … + β n − 1 L_{ESO}(s)=s^{n+1}+\beta_1 s^n + \beta_2 s^{n-1}+…+\beta_{n-1}
L E S O ( s ) = s n + 1 + β 1 s n + β 2 s n − 1 + … + β n − 1
将极点都配置到左半轴同一位置,可以将调节参数缩减为
L E S O ( s ) = ( s + w o ) n + 1 = 0 L_{ESO}(s)=(s+w_o)^{n+1}=0
L E S O ( s ) = ( s + w o ) n + 1 = 0
其中 w o w_o w o β \beta β
输入为 u , y u, y u , y
输出为
z 1 ( k + 1 ) = z 1 ( k ) + h z 1 ˙ ( k ) = z 1 ( k ) + h ( − β 1 z 1 ( k ) + z 2 ( k ) + β 1 y ) z 2 ( k + 1 ) = z 2 ( k ) + h z 2 ˙ ( k ) = z 2 ( k ) + h ( − β 2 z 1 ( k ) + z 3 ( k ) + β 2 y ) z 3 ( k + 1 ) = z 3 ( k ) + h z 3 ˙ ( k ) = z 3 ( k ) + h ( − β 3 z 1 ( k ) + z 4 ( k ) + β 3 y ) z 4 ( k + 1 ) = z 4 ( k ) + h z 4 ˙ ( k ) = z 4 ( k ) + h ( − β 4 z 1 ( k ) + z 5 ( k ) + b 0 u + β 4 y ) z 5 ( k + 1 ) = z 5 ( k ) + h z 5 ˙ ( k ) = z 5 ( k ) + h ( − β 5 z 1 ( k ) + β 5 y ) z_1(k+1)=z_1(k)+h\dot{z_1}(k)=z_1(k)+h(-\beta_1z_1(k)+z_2(k)+\beta_1y)\\z_2(k+1)=z_2(k)+h\dot{z_2}(k)=z_2(k)+h(-\beta_2z_1(k)+z_3(k)+\beta_2y)\\z_3(k+1)=z_3(k)+h\dot{z_3}(k)=z_3(k)+h(-\beta_3z_1(k)+z_4(k)+\beta_3y)\\z_4(k+1)=z_4(k)+h\dot{z_4}(k)=z_4(k)+h(-\beta_4z_1(k)+z_5(k)+b_0u+\beta_4y)\\z_5(k+1)=z_5(k)+h\dot{z_5}(k)=z_5(k)+h(-\beta_5z_1(k)+\beta_5y)
z 1 ( k + 1 ) = z 1 ( k ) + h z 1 ˙ ( k ) = z 1 ( k ) + h ( − β 1 z 1 ( k ) + z 2 ( k ) + β 1 y ) z 2 ( k + 1 ) = z 2 ( k ) + h z 2 ˙ ( k ) = z 2 ( k ) + h ( − β 2 z 1 ( k ) + z 3 ( k ) + β 2 y ) z 3 ( k + 1 ) = z 3 ( k ) + h z 3 ˙ ( k ) = z 3 ( k ) + h ( − β 3 z 1 ( k ) + z 4 ( k ) + β 3 y ) z 4 ( k + 1 ) = z 4 ( k ) + h z 4 ˙ ( k ) = z 4 ( k ) + h ( − β 4 z 1 ( k ) + z 5 ( k ) + b 0 u + β 4 y ) z 5 ( k + 1 ) = z 5 ( k ) + h z 5 ˙ ( k ) = z 5 ( k ) + h ( − β 5 z 1 ( k ) + β 5 y )
LSEF
令
e 1 = x 1 − z 1 e 2 = x 2 − z 2 e 3 = x 3 − z 3 e 4 = x 4 − z 4 u 0 = a 1 e 1 + a 2 e 2 + a 3 e 3 + a 4 e 4 u = u 0 − z 5 b 0 e_1 = x_1 - z_1\\e_2=x_2-z_2\\e_3=x_3-z_3\\e_4=x_4-z_4\\u_0 = a_1 e_1+a_2e_2+a_3e_3+a_4e_4\\u=\frac{u_0-z_5}{b_0}
e 1 = x 1 − z 1 e 2 = x 2 − z 2 e 3 = x 3 − z 3 e 4 = x 4 − z 4 u 0 = a 1 e 1 + a 2 e 2 + a 3 e 3 + a 4 e 4 u = b 0 u 0 − z 5
其中 a 1 a_1 a 1
L S E F ( s ) = s n + a n s n − 1 + … + a 2 s + a 1 L_{SEF}(s)=s^n+a_ns^{n-1}+…+a_2s+a_1
L S E F ( s ) = s n + a n s n − 1 + … + a 2 s + a 1
将特征值统一配置在左半实轴同一位置,得到
L S E F ( s ) = ( s + w c ) n L_{SEF}(s)=(s+w_c)^{n}
L S E F ( s ) = ( s + w c ) n
其中 w c w_c w c
LTD
形式为:
{ e 1 = x 1 − v d x 1 d t = − r ∗ f a l ( e 1 , α 1 , δ 1 ) \left\{\begin{aligned}e_1&=x_1-v\\\frac{dx_1}{dt}&=-r*fal(e_1,\alpha_1,\delta_1)\end{aligned}\right.
⎩ ⎪ ⎨ ⎪ ⎧ e 1 d t d x 1 = x 1 − v = − r ∗ f a l ( e 1 , α 1 , δ 1 )
离散化处理之后为
{ e 1 ( k ) = x 1 ( k ) − v ( k ) x 1 ( k + 1 ) = − r T f a l ( e 1 ( k ) , α 1 , δ 1 ) + x 1 ( k ) \left\{\begin{aligned}e_1(k)&=x_1(k)-v(k)\\x_1(k+1)&=-rTfal(e_1(k),\alpha_1,\delta_1)+x_1(k)\end{aligned}\right.
{ e 1 ( k ) x 1 ( k + 1 ) = x 1 ( k ) − v ( k ) = − r T f a l ( e 1 ( k ) , α 1 , δ 1 ) + x 1 ( k )
其中
f a l ( e , α , δ ) = { ∣ e ∣ α s i g n ( e ) ∣ e ∣ > δ e δ 1 − α ∣ e ∣ ≤ δ fal(e, \alpha,\delta)=\left\{\begin{aligned}&{|e|}^{\alpha}sign(e) && |e| > \delta\\&\frac{e}{\delta^{1-\alpha}} && |e| \leq \delta\end{aligned}\right.
f a l ( e , α , δ ) = ⎩ ⎪ ⎨ ⎪ ⎧ ∣ e ∣ α s i g n ( e ) δ 1 − α e ∣ e ∣ > δ ∣ e ∣ ≤ δ
其中, f a l fal f a l α \alpha α α > 1 \alpha>1 α > 1 0 < α < 1 0<\alpha<1 0 < α < 1 α \alpha α δ \delta δ δ \delta δ δ \delta δ
LESO
形式为:
{ e 2 = z 21 − y d z 21 d t = z 22 − β 21 f a l ( e 2 , α 2 , δ 2 ) + b u d z 22 d t = − β 22 f a l ( e 2 , α 2 , δ 2 ) \left\{\begin{aligned}e_2&=z_{21}-y\\\frac{dz_{21}}{dt}&=z_{22}-\beta_{21}fal(e_2, \alpha_2,\delta_2)+bu\\\frac{dz_{22}}{dt} &= -\beta_{22}fal(e_2, \alpha_2,\delta_2)\end{aligned}\right.
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ e 2 d t d z 2 1 d t d z 2 2 = z 2 1 − y = z 2 2 − β 2 1 f a l ( e 2 , α 2 , δ 2 ) + b u = − β 2 2 f a l ( e 2 , α 2 , δ 2 )
其中
{ β 21 = 2 ∗ ω 0 β 22 = ω 0 2 \left\{\begin{aligned}\beta_{21}&=2*\omega_0\\\beta_{22}&=\omega_0^2\end{aligned}\right.
{ β 2 1 β 2 2 = 2 ∗ ω 0 = ω 0 2
离散化处理之后
{ e 2 ( k ) = z 21 ( k ) − y ( k ) z 21 ( k + 1 ) = T ( z 22 ( k ) − β 21 f a l ( e 2 , α 2 , δ 2 ) + b u ) + z 21 ( k ) z 22 ( k + 1 ) = − T β 22 f a l ( e 2 , α 2 , δ 2 ) + z 22 ( k ) \left\{\begin{aligned}e_2(k)&=z_{21}(k)-y(k)\\z_{21}(k+1)&=T(z_{22}(k)-\beta_{21}fal(e_2,\alpha_2,\delta_2)+bu)+z_{21}(k)\\z_{22}(k+1)&=-T\beta_{22}fal(e_2,\alpha_2,\delta_2)+z_{22}(k)\end{aligned}\right.
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ e 2 ( k ) z 2 1 ( k + 1 ) z 2 2 ( k + 1 ) = z 2 1 ( k ) − y ( k ) = T ( z 2 2 ( k ) − β 2 1 f a l ( e 2 , α 2 , δ 2 ) + b u ) + z 2 1 ( k ) = − T β 2 2 f a l ( e 2 , α 2 , δ 2 ) + z 2 2 ( k )
{ z 21 → y z 22 → f \left\{\begin{aligned}z_{21}→y\\z_{22}→f\end{aligned}\right.
{ z 2 1 → y z 2 2 → f
输出为
{ z 21 ( k + 1 ) z 22 ( k + 1 ) \left\{\begin{aligned}z_{21}(k+1)\\z_{22}(k+1)\end{aligned}\right.
{ z 2 1 ( k + 1 ) z 2 2 ( k + 1 )
LSEF
形式为:
{ e 3 = x 1 − z 21 u 0 = k p ∗ f a l ( e 3 , α 3 , δ 3 ) u = u 0 − z 22 b u = u 0 − z 22 b \left\{\begin{aligned}e_3&=x_1-z_{21}\\u_0&=kp*fal(e_3,\alpha_3,\delta_3)\\u&=\frac{u_0-z_{22}}{b}\\u&=u_0-\frac{z_{22}}{b}\end{aligned}\right.
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ e 3 u 0 u u = x 1 − z 2 1 = k p ∗ f a l ( e 3 , α 3 , δ 3 ) = b u 0 − z 2 2 = u 0 − b z 2 2
输出 u u u
离散化处理:这里应当是依据于最新状态来计算的
{ e 3 ( k ) = x 1 ( k ) − z 21 ( k ) u 0 ( k ) = k p ∗ f a l ( e 3 ( k ) , α 3 , δ 3 ) u ( k ) = u 0 ( k ) − z 22 ( k ) b u ( k ) = u 0 ( k ) − z 22 ( k ) b \left\{\begin{aligned}e_3(k)&=x_1(k)-z_{21}(k)\\u_0(k)&=kp*fal(e_3(k),\alpha_3,\delta_3)\\u(k)&=\frac{u_0(k)-z_{22}(k)}{b}\\u(k)&=u_0(k)-\frac{z_{22}(k)}{b}\end{aligned}\right.
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ e 3 ( k ) u 0 ( k ) u ( k ) u ( k ) = x 1 ( k ) − z 2 1 ( k ) = k p ∗ f a l ( e 3 ( k ) , α 3 , δ 3 ) = b u 0 ( k ) − z 2 2 ( k ) = u 0 ( k ) − b z 2 2 ( k )
LTD
{ d x 1 d t = x 2 d x 2 d t = − r ∗ s i g n ( x 1 − v + x 2 ∣ x 2 ∣ 2 r ) \left\{\begin{aligned}\frac{dx_1}{dt}&=x_2\\\frac{dx_2}{dt}&=-r*sign(x_1-v+\frac{x_2|x_2|}{2r})\end{aligned}\right.
⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ d t d x 1 d t d x 2 = x 2 = − r ∗ s i g n ( x 1 − v + 2 r x 2 ∣ x 2 ∣ )
为了避免在原点附近的颤振,将符号函数 s i g n sign s i g n s a t sat s a t
{ d x 1 d t = x 2 d x 2 d t = − r ∗ s a t ( x 1 − v + x 2 ∣ x 2 ∣ 2 r , δ ) \left\{\begin{aligned}\frac{dx_1}{dt}&=x_2\\\frac{dx_2}{dt}&=-r*sat(x_1-v+\frac{x_2|x_2|}{2r}, \delta)\end{aligned}\right.
⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ d t d x 1 d t d x 2 = x 2 = − r ∗ s a t ( x 1 − v + 2 r x 2 ∣ x 2 ∣ , δ )
其中
s a t ( x , δ ) = { s i g n ( x ) ∣ x ∣ ≥ δ x δ ∣ x ∣ < δ sat(x, \delta)=\left\{\begin{aligned}&sign(x)&&|x|\geq\delta\\&\frac{x}{\delta}&&|x|<\delta\end{aligned}\right.
s a t ( x , δ ) = ⎩ ⎪ ⎨ ⎪ ⎧ s i g n ( x ) δ x ∣ x ∣ ≥ δ ∣ x ∣ < δ
对应的离散化函数为
{ x 1 ( k + 1 ) = x 1 ( k ) + h ∗ x 2 ( k ) x 2 ( k + 1 ) = x 2 ( k ) + h ∗ f s t ( x 1 ( k ) − v ( k ) , x 2 ( k ) , r , h 1 ) \left\{\begin{aligned}x_1(k+1)&=x_1(k)+h*x_2(k)\\x_2(k+1)&=x_2(k)+h*fst(x_1(k)-v(k),x_2(k),r,h1)\end{aligned}\right.
{ x 1 ( k + 1 ) x 2 ( k + 1 ) = x 1 ( k ) + h ∗ x 2 ( k ) = x 2 ( k ) + h ∗ f s t ( x 1 ( k ) − v ( k ) , x 2 ( k ) , r , h 1 )
其中 r r r h 1 h_1 h 1
{ d = r ∗ h 1 d 0 = h 1 ∗ d y = x 1 ( k ) + h 1 ∗ x 2 ( k ) − v ( k ) a 0 = d 2 + 8 r ∣ y ∣ a = { x 2 ( k ) + a 0 − d 2 s i g n ( y ) ∣ y ∣ > d 0 x 2 ( k ) + y h 1 ∣ y ∣ ≤ d 0 f s t ( x 1 ( k ) − v ( k ) , x 2 , r , h 1 ) = { − r ∗ s i g n ( a ) ∣ a ∣ > d − r a d ∣ a ∣ ≤ d \left\{\begin{aligned}d&=r*h_1\\d_0&=h_1*d\\y&=x_1(k)+h_1*x_2(k)-v(k)\\a_0&=\sqrt{d^2+8r|y|}\\a&=\left\{\begin{aligned}x_2(k)+\frac{a_0-d}{2}sign(y)&&|y|>d_0\\x_2(k)+\frac{y}{h_1}&&|y|\leq d_0\end{aligned}\right.\\fst(x_1(k)-v(k),x_2,r,h_1)&=\left\{\begin{aligned}-r*sign(a)&&|a|>d\\-r\frac{a}{d}&&|a|\leq d\end{aligned}\right.\end{aligned}\right.
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ d d 0 y a 0 a f s t ( x 1 ( k ) − v ( k ) , x 2 , r , h 1 ) = r ∗ h 1 = h 1 ∗ d = x 1 ( k ) + h 1 ∗ x 2 ( k ) − v ( k ) = d 2 + 8 r ∣ y ∣ = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ x 2 ( k ) + 2 a 0 − d s i g n ( y ) x 2 ( k ) + h 1 y ∣ y ∣ > d 0 ∣ y ∣ ≤ d 0 = ⎩ ⎪ ⎨ ⎪ ⎧ − r ∗ s i g n ( a ) − r d a ∣ a ∣ > d ∣ a ∣ ≤ d
其中 r r r h 1 h_1 h 1
当 h 1 > h h_1>h h 1 > h
通过查阅资料(自抗扰控制技术)离散化函数也可以写成这样:
{ x 1 ( k + 1 ) = x 1 ( k ) + h x 2 ( k ) x 2 ( k + 1 ) = x 2 ( k ) + h ∗ f h a n ( x 1 ( k ) − v ( k ) , x 2 ( k ) , r , h 1 ) \left\{\begin{aligned}x_1(k+1)&=x_1(k)+hx_2(k)\\x_2(k+1)&=x_2(k)+h*fhan(x_1(k)-v(k),x_2(k),r,h1)\end{aligned}\right.
{ x 1 ( k + 1 ) x 2 ( k + 1 ) = x 1 ( k ) + h x 2 ( k ) = x 2 ( k ) + h ∗ f h a n ( x 1 ( k ) − v ( k ) , x 2 ( k ) , r , h 1 )
这里的 h 1 h_1 h 1 h h h
f s t ( x 1 ( k ) − v ( k ) , x 2 , r , h 1 ) = { d = r ∗ h 1 2 a 0 = h 1 ∗ x 2 y = x 1 ( k ) − v ( k ) + a 0 a 1 = d ( d + 8 ∣ y ∣ ) a 2 = a 0 + a 1 − d 2 s i g n ( y ) a = ( a 0 + y ) f s g ( y , d ) + a 2 ( 1 − f s g ( y , d ) ) f h a n = − r a d f s g ( a , d ) − r ∗ s i g n ( a ) ( 1 − f s g ( a , d ) ) f s g ( x , d ) = s i g n ( x + d ) − s i g n ( x − d ) 2 fst(x_1(k)-v(k),x_2,r,h_1)=\left\{\begin{aligned}d&=r*h_1^2\\a_0&=h_1*x_2\\y&=x_1(k)-v(k)+a_0\\a_1&=\sqrt{d(d+8|y|)}\\a_2&=a_0+\frac{a_1-d}{2}sign(y)\\a&=(a_0+y)fsg(y,d)+a_2(1-fsg(y,d))\\fhan&=-r\frac{a}{d}fsg(a,d)-r*sign(a)(1-fsg(a,d))\\fsg(x,d)&=\frac{sign(x+d)-sign(x-d)}{2}\end{aligned}\right.
f s t ( x 1 ( k ) − v ( k ) , x 2 , r , h 1 ) = ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ d a 0 y a 1 a 2 a f h a n f s g ( x , d ) = r ∗ h 1 2 = h 1 ∗ x 2 = x 1 ( k ) − v ( k ) + a 0 = d ( d + 8 ∣ y ∣ ) = a 0 + 2 a 1 − d s i g n ( y ) = ( a 0 + y ) f s g ( y , d ) + a 2 ( 1 − f s g ( y , d ) ) = − r d a f s g ( a , d ) − r ∗ s i g n ( a ) ( 1 − f s g ( a , d ) ) = 2 s i g n ( x + d ) − s i g n ( x − d )
LESO
{ e 2 = z 21 − y d z 21 d t = z 22 − β 21 ∗ e 2 d z 22 d t = z 23 − β 22 ∗ f a l ( e 2 , α 2 , δ 2 ) + b ∗ u d z 23 d t = − β 23 ∗ f a l ( e 2 , α 3 , δ 3 ) \left\{\begin{aligned}e_2&=z_{21}-y\\\frac{dz_{21}}{dt}&=z_{22}-\beta_{21}*e_2\\\frac{dz_{22}}{dt}&=z_{23}-\beta_{22}*fal(e_2,\alpha_2,\delta_2)+b*u\\\frac{dz_{23}}{dt}&=-\beta_{23}*fal(e_2,\alpha_3,\delta_3)\end{aligned}\right.
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ e 2 d t d z 2 1 d t d z 2 2 d t d z 2 3 = z 2 1 − y = z 2 2 − β 2 1 ∗ e 2 = z 2 3 − β 2 2 ∗ f a l ( e 2 , α 2 , δ 2 ) + b ∗ u = − β 2 3 ∗ f a l ( e 2 , α 3 , δ 3 )
式中的 β \beta β α 3 < α 2 \alpha_3<\alpha_2 α 3 < α 2 δ 2 \delta_2 δ 2 5 T ≤ δ 2 ≤ 10 T 5T\leq \delta_2\leq 10T 5 T ≤ δ 2 ≤ 1 0 T
{ β 21 = 3 ∗ ω o β 22 = 3 ∗ ω o 2 β 23 = ω o 3 \left\{\begin{aligned}\beta_{21}&=3*\omega_o\\\beta_{22}&=3*\omega_o^2\\\beta_{23}&=\omega_o^3\end{aligned}\right.
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ β 2 1 β 2 2 β 2 3 = 3 ∗ ω o = 3 ∗ ω o 2 = ω o 3
离散化处理
{ z 21 ( k + 1 ) = h ( z 22 ( k ) − β 21 ∗ e 2 ( k ) ) + z 21 ( k ) z 22 ( k + 1 ) = h ( z 23 ( k ) − β 22 f a l ( e 2 ( k ) , α 2 , δ 2 ) + b u ( k ) ) + z 22 ( k ) z 23 ( k + 1 ) = h ( − β 23 ∗ f a l ( e 2 ( k ) , α 3 , δ 3 ) ) + z 23 ( k ) \left\{\begin{aligned}z_{21}(k+1)&=h(z_{22}(k)-\beta_{21}*e_2(k)) + z_{21}(k)\\z_{22}(k+1)&=h(z_{23}(k)-\beta_{22}fal(e_2(k),\alpha_2,\delta_2)+bu(k)) + z_{22}(k)\\z_{23}(k+1)&=h(-\beta_{23}*fal(e_2(k),\alpha_3,\delta_3)) + z_{23}(k)\end{aligned}\right.
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ z 2 1 ( k + 1 ) z 2 2 ( k + 1 ) z 2 3 ( k + 1 ) = h ( z 2 2 ( k ) − β 2 1 ∗ e 2 ( k ) ) + z 2 1 ( k ) = h ( z 2 3 ( k ) − β 2 2 f a l ( e 2 ( k ) , α 2 , δ 2 ) + b u ( k ) ) + z 2 2 ( k ) = h ( − β 2 3 ∗ f a l ( e 2 ( k ) , α 3 , δ 3 ) ) + z 2 3 ( k )
其中
f a l ( e , α , δ ) = { ∣ e ∣ α s i g n ( e ) ∣ e ∣ > δ e δ 1 − α ∣ e ∣ ≤ δ fal(e, \alpha,\delta)=\left\{\begin{aligned}&{|e|}^{\alpha}sign(e) && |e| > \delta\\&\frac{e}{\delta^{1-\alpha}} && |e| \leq \delta\end{aligned}\right.
f a l ( e , α , δ ) = ⎩ ⎪ ⎨ ⎪ ⎧ ∣ e ∣ α s i g n ( e ) δ 1 − α e ∣ e ∣ > δ ∣ e ∣ ≤ δ
LSEF
总共有三种非线性的反馈控制规律
u 0 = { β 1 e 1 + β 2 e 2 ∑ i = 1 n β i f a l ( x i − z i , α i , d ) − f h a n ( e 1 , e 2 , r , h ) − f h a n ( e 1 , c e 2 , r , h ) u_0=\left\{\begin{aligned}&\beta_1e_1+\beta_2e_2\\&\sum_{i=1}^n\beta_ifal(x_i-z_i,\alpha_i,d)\\&-fhan(e_1,e_2,r,h)\\&-fhan(e_1,ce_2,r,h)\end{aligned}\right.
u 0 = ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ β 1 e 1 + β 2 e 2 i = 1 ∑ n β i f a l ( x i − z i , α i , d ) − f h a n ( e 1 , e 2 , r , h ) − f h a n ( e 1 , c e 2 , r , h )
其中
e 0 = ∫ 0 t e 1 ( t ) d t e_0=\int^{t}_{0}{e_1(t)dt}
e 0 = ∫ 0 t e 1 ( t ) d t
这里的 u 0 u_0 u 0
其中
f h a n ( e 1 , e 2 , r , h ) = { d = r ∗ h 2 a 0 = h 1 ∗ e 2 y = e 1 + a 0 a 1 = d ∗ ( d + 8 ∣ y ∣ ) a 2 = a 0 + a 1 − d 2 s i g n ( y ) a = ( a 0 + y ) f s g ( y , d ) + a 2 ( 1 − f s g ( y , d ) ) f h a n = − r a d f s g ( a , d ) − r ∗ s i g n ( a ) ( 1 − f s g ( a , d ) ) f s g ( x , d ) = s i g n ( x + d ) − s i g n ( x − d ) 2 fhan(e_1,e_2,r,h)=\left\{\begin{aligned}d&=r*h^2\\a_0&=h_1*e_2\\y&=e_1+a_0\\a_1&=\sqrt{d*(d+8|y|)}\\a_2&=a_0+\frac{a_1-d}{2}sign(y)\\a&=(a_0+y)fsg(y,d)+a_2(1-fsg(y,d))\\fhan&=-r\frac{a}{d}fsg(a,d)-r*sign(a)(1-fsg(a,d))\\fsg(x,d)&=\frac{sign(x+d)-sign(x-d)}{2}\end{aligned}\right.
f h a n ( e 1 , e 2 , r , h ) = ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ d a 0 y a 1 a 2 a f h a n f s g ( x , d ) = r ∗ h 2 = h 1 ∗ e 2 = e 1 + a 0 = d ∗ ( d + 8 ∣ y ∣ ) = a 0 + 2 a 1 − d s i g n ( y ) = ( a 0 + y ) f s g ( y , d ) + a 2 ( 1 − f s g ( y , d ) ) = − r d a f s g ( a , d ) − r ∗ s i g n ( a ) ( 1 − f s g ( a , d ) ) = 2 s i g n ( x + d ) − s i g n ( x − d )
u u u
u = { u 0 − z 23 b u 0 − z 23 b u=\left\{\begin{aligned}&\frac{u_0-z_{23}}{b}\\&u_0-\frac{z_{23}}{b}\end{aligned}\right.
u = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ b u 0 − z 2 3 u 0 − b z 2 3
离散化处理之后
{ u 0 = { β 1 e 1 + β 2 e 2 ∑ i = 1 n β i f a l ( x i − z i , α i , d ) − f h a n ( e 1 , e 2 , r , h ) − f h a n ( e 1 , c e 2 , r , h ) u ( k ) = { u 0 ( k ) − z 23 ( k ) b u 0 ( k ) − z 23 ( k ) b \left\{\begin{aligned}u_0&=\left\{\begin{aligned}&\beta_1e_1+\beta_2e_2\\&\sum_{i=1}^n\beta_ifal(x_i-z_i,\alpha_i,d)\\&-fhan(e_1,e_2,r,h)\\&-fhan(e_1,ce_2,r,h)\end{aligned}\right.\\u(k)&=\left\{\begin{aligned}&\frac{u_0(k)-z_{23}(k)}{b}\\&u_0(k)-\frac{z_{23}(k)}{b}\end{aligned}\right.\end{aligned}\right.
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ u 0 u ( k ) = ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ β 1 e 1 + β 2 e 2 i = 1 ∑ n β i f a l ( x i − z i , α i , d ) − f h a n ( e 1 , e 2 , r , h ) − f h a n ( e 1 , c e 2 , r , h ) = ⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ b u 0 ( k ) − z 2 3 ( k ) u 0 ( k ) − b z 2 3 ( k )