github仓库

前言

Linear Quadratic Gaussian

在实际系统中，噪声是不可避免的，在噪声的影响下，系统状态方程可以写作

{X˙=AX+Bu+Gwy=CX+Du+Hw+v\left\{\begin{aligned}&\dot{X}=AX+Bu+Gw\\&y=CX+Du+Hw+v\end{aligned}\right.

其中 w,vw,v 均被当作为白噪声

如果我们假设噪声是均值为0高斯分布（事实上很多时候确实近似服从高斯分布，想想为什么呢？）由于系统噪声和输出噪声的存在，状态不能完美的衰减为0。我们就希望优化损失函数的期望，即

J=E{lim⁡T→∞1T∫0T[XTQX+UTRU]dt}J=E\{\underset{T\rightarrow\infty}{\lim}\frac{1}{T}\int_0^T[X^TQX+U^TRU]dt\}

LQG 控制器实际上就是一个最优二次型线性调节器+一个最优状态估计器（卡尔曼滤波器）而得到的一个控制器，即 LQR+KF

而 LQG 控制器相当于是将两个系统分离，LQR 与 KF 分离，而 LQR 是依旧是依据原系统所建立的一个控制系统，不过系统的观测值需要经过 KF 预估

KF

在 LQG 框观测器架中的卡尔曼滤波器，指的是一个最优状态观测器，这里的观测器是现代控制理论—状态空间方程中的最常见的观测器——龙伯格观测器，但是后者极点是自由配置的，并且没有考虑噪声的影响，并不是最优

对于一个系统

x˙=Ax+Bu+Gwy=Cx+Du+Hw+v\dot{x}=Ax+Bu+Gw\\y=Cx+Du+Hw+v

其中 ww 是过程噪声， vv 是观测噪声，它们被假设是符合高斯（Gauss）分布的。 G,HG,H 是常系数矩阵，用于描述 xx 中各部分受到噪声强度不一致的情况，很多地方 HH 被认为是一个 0 矩阵，区别不大

假设

  • 系统可观测
  • 噪声符合高斯分布，且协方差矩阵为 E(wwT)=Qk,E(vvT)=Rk,E(wvT)=NkE(ww^T)=Q_k,E(vv^T)=R_k,E(wv^T)=N_k

对于给定观测器动态和代价函数

x^˙=Ax^+Bu+L(y−Cx^−Du)y^=x^J′=lim⁡t→∞E{(x−x^)(x−x^)T}\dot{\hat x}=A\hat{x}+Bu+L(y-C\hat{x}-Du)\\\\ \hat{y}=\hat{x}\\\\ J'=\underset{t\rightarrow \infty}{\lim}E\{(x-\hat{x})(x-\hat x)^T\}

需要寻找一个常系数矩阵使得 J′J' 最小，最后得到

L=(PCT+N‾)R‾−1L=(PC^T+\overline{N})\overline{R}^{-1}

其中

R‾=Rk+HNk+NkTHT+HQkHTN‾=G(QkHT+Nk)\overline{R}=R_k+HN_k+N_k^TH^T+HQ_kH^T\\\overline{N}=G(Q_kH^T+N_k)

同时 PP 是以下 Riccati 方程的解，并且 PP 是一个对称正定矩阵

ATP+PA−(PB+Nk)Rk−1(BTP+NkT)+Qk=0A^TP+PA-(PB+N_k)R_k^{-1}(B^TP+N_k^T)+Q_k=0

使用得到的这个 LL 的最优观测器，就是 LQG 框架使用的卡尔曼滤波器

LQG

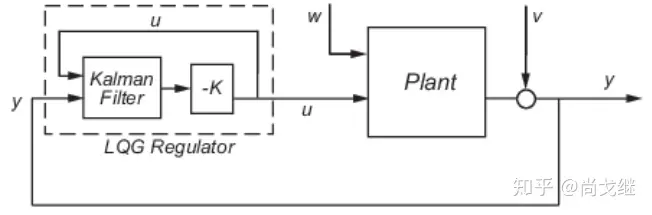
v2-08a6922f338cace58c7b03b433517171_720w.webp

其中的 -K 就是 LQR 控制器，而 w 是过程噪声， v 是观测噪声

分离性原理

假设系统可控可观测

LQR 是一种最优的线性状态反馈， KF 是一种最优的状态估计，直接将两级串联闭环系统可以写作

[x˙x^˙]=Alqg[xx^]+Glqg[wv]y=Clqg[xx^]+Hlqg[wv]\begin{bmatrix}\dot{x}\\\dot{\hat x}\end{bmatrix}=A_{lqg}\begin{bmatrix}x\\\hat x\end{bmatrix}+G_{lqg}\begin{bmatrix}w\\v\end{bmatrix}\\\\ y=C_{lqg}\begin{bmatrix}x\\\hat x\end{bmatrix}+H_{lqg}\begin{bmatrix}w\\v\end{bmatrix}

其中

Alqg=[A−BFLCA−BF−LC]Glqg=[G0LHL]Blqg=[BB−LD]Clqg=[C−DF00]Hlqg=[H00I]A_{lqg}=\begin{bmatrix}A&-BF\\LC&A-BF-LC\end{bmatrix}\\\\ G_{lqg}=\begin{bmatrix}G&0\\LH&L\end{bmatrix}\\\\ B_{lqg}=\begin{bmatrix}B\\B-LD\end{bmatrix}\\\\ C_{lqg}=\begin{bmatrix}C&-DF\\0&0\end{bmatrix}\\\\ H_{lqg}=\begin{bmatrix}H&0\\0&I\end{bmatrix}

此时引入观测器误差 δ=x−x^\delta=x-\hat{x}，可以得到

[xδ]=[I0I−I][xx^]⇓[I0I−I][xδ]=[xx^]Ctransform=[I0I−I]\begin{bmatrix}x\\\delta\end{bmatrix}=\begin{bmatrix}I&0\\I&-I\end{bmatrix}\begin{bmatrix}x\\\hat x\end{bmatrix}\\\\ \Downarrow\\\\ \begin{bmatrix}I&0\\I&-I\end{bmatrix}\begin{bmatrix}x\\\delta\end{bmatrix}=\begin{bmatrix}x\\\hat x\end{bmatrix}\\\\ C_{transform}=\begin{bmatrix}I&0\\I&-I\end{bmatrix}

所以带入上式可以得到

[x˙δ˙]=CtransformAlqgCtransform[xδ]+CtransformGlqg[wv]y=ClqgCtransform[xδ]+Hlqg[wv]⇓[x˙δ˙]=[A−BFBF0A−LC][xδ]+CtransformBlqg[wv]⇓xa˙=Aaxa+GaWy=Caxa+HaW\begin{bmatrix}\dot{x}\\\dot{\delta}\end{bmatrix}=C_{transform}A_{lqg}C_{transform}\begin{bmatrix}x\\\delta\end{bmatrix}+C_{transform}G_{lqg}\begin{bmatrix}w\\v\end{bmatrix}\\\\ y=C_{lqg}C_{transform}\begin{bmatrix}x\\\delta\end{bmatrix}+H_{lqg}\begin{bmatrix}w\\v\end{bmatrix}\\\\ \Downarrow\\\\ \begin{bmatrix}\dot{x}\\\dot{\delta}\end{bmatrix}=\begin{bmatrix}A-BF&BF\\0&A-LC\end{bmatrix}\begin{bmatrix}x\\\delta\end{bmatrix}+C_{transform}B_{lqg}\begin{bmatrix}w\\v\end{bmatrix}\\\\ \Downarrow\\\\ \dot{x_a}=A_ax_a+G_aW\\\\ y=C_ax_a+H_aW

由于 A−BFA-BF 和 A−LCA-LC 都是稳定的，即它们的特征值都严格小于 0，根据分块矩阵的特征值得计算规则，这个大的矩阵也是稳定的。这就意味着可以使 LQR 和 KF 级联，得到一个稳定的系统，这就是分离性原理。

例子

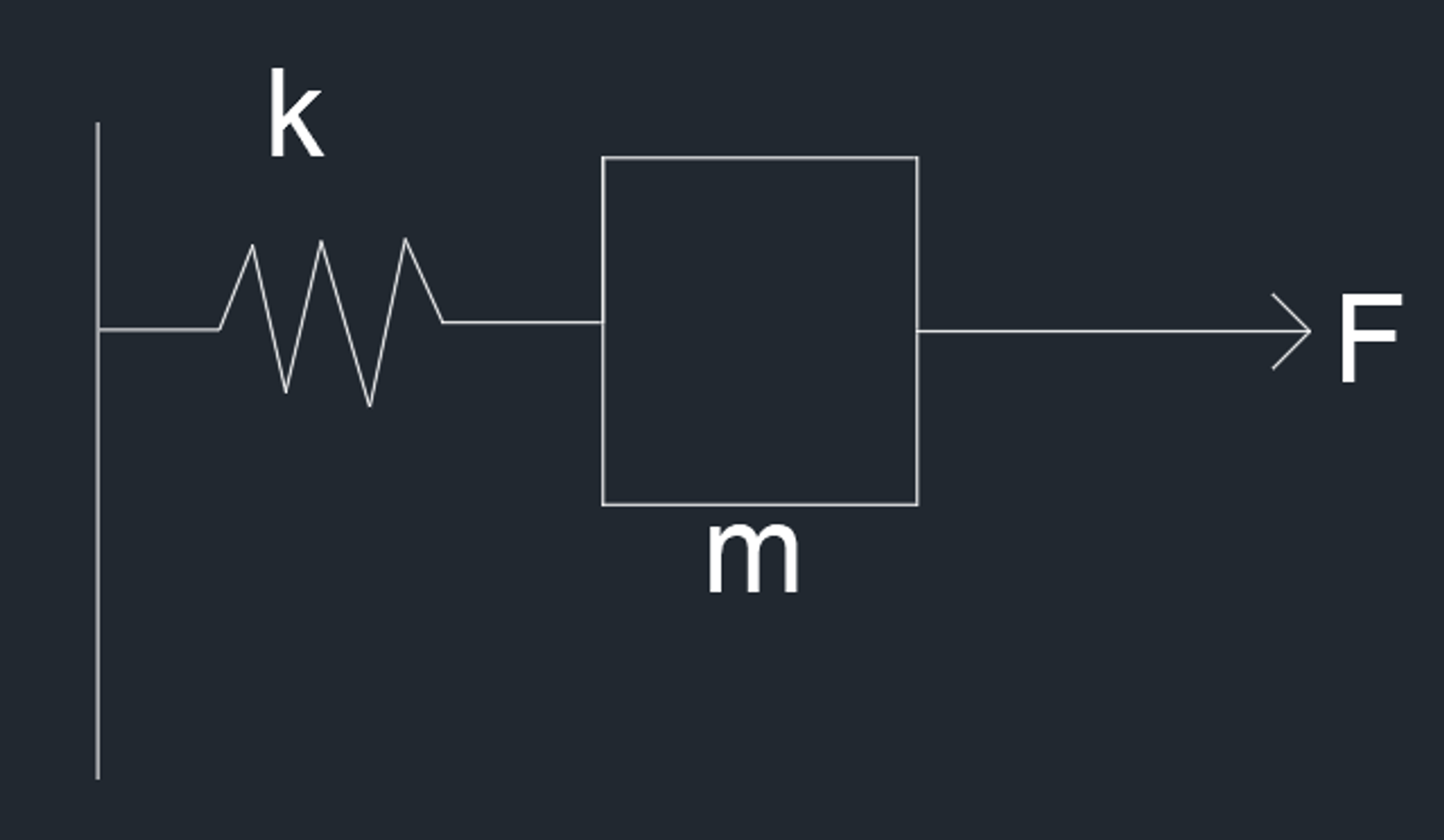
Untitled

由此图列出系统状态方程

[x1˙x2˙]=[01km0][x1x2]+[01m]u+[11]wy=[10][x1x2]+[0]w+v\begin{bmatrix}\dot{x_1}\\\dot{x_2}\end{bmatrix}=\begin{bmatrix}0&1\\\frac{k}{m}&0\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}+\begin{bmatrix}0\\\frac{1}{m}\end{bmatrix}u+\begin{bmatrix}1\\1\end{bmatrix}w\\\\ y=\begin{bmatrix}1&0\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}+\begin{bmatrix}0\end{bmatrix}w+v

首先是建立 LQR 控制器，先不考虑噪声

[x1˙x2˙]=[01km0][x1x2]+[01m]uy=[10][x1x2]\begin{bmatrix}\dot{x_1}\\\dot{x_2}\end{bmatrix}=\begin{bmatrix}0&1\\\frac{k}{m}&0\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}+\begin{bmatrix}0\\\frac{1}{m}\end{bmatrix}u\\\\ y=\begin{bmatrix}1&0\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}

根据系统代价函数

J=∫0∞[xTQx+uTRu]dtJ=\int^\infty_0[x^TQx+u^TRu]dt

设定相应的权重系数矩阵 Q 和 R，并且在matlab中可以直接调用函数 lqr 来获得对应的线性反馈控制器

1
K = lqr(A, B, Q, R);

推导过程可以查看 LQR线性二次调节器——系统输入线性化

建立 KF 滤波器

x^k∣k−1=Fkx^k−1∣k−1Pk∣k−1=FkPk−1∣k−1FkT+QkKk=Pk∣k−1HkT(HkPk∣k−1HkT+Rk)−1x^k∣k=x^k∣k−1+Kk(zk−Hkx^k∣k−1)Pk∣k=(I−KkHk)Pk∣k−1\hat{x}_{k|k-1}=F_k\hat{x}_{k-1|k-1}\\\\ P_{k|k-1}=F_kP_{k-1|k-1}F_k^T+Q_k\\\\ K_k=P_{k|k-1}H_k^T(H_kP_{k|k-1}H_k^T+R_k)^{-1}\\\\ \hat{x}_{k|k}=\hat{x}_{k|k-1}+K_k(z_k-H_k\hat{x}_{k|k-1})\\\\ P_{k|k}=(I-K_kH_k)P_{k|k-1}

根据公式，可以得到 x^\hat{x}，然后与 lqr 的线性反馈控制器作用，得到对系统的控制

关于 KF 可以看 卡尔曼滤波 KF

参考

线性二次积分控制 - MATLAB lqg - MathWorks 中国