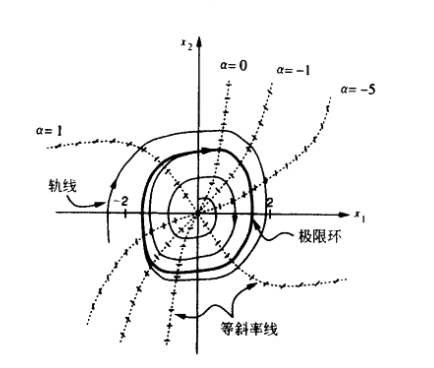
控制器原理
对于一个系统
x˙=ax2+ux→xd
可以设定 e=xd−x,并且使 e→0,定义李雅普诺夫函数
V(e)=21e2:PD
得到
V˙(e)=ee˙=e(x˙d−ax2−u)
要使得上式负定,可以令 e˙=−ke ,就可以设置 u=x˙d−ax2+ke,化简上式为
V˙(e)=−ke2:ND
但是对于上述例子,如果 a 是未知的,或者是缓慢变化的数字(a˙=0)就难以控制,所以需要自适应控制器,可以引入估计值 a^ 和估计误差 a=a−a^,所以 a˙=a˙−a^˙=−a^˙ 。可以设置李雅普诺夫函数
V(e,a)=21e2+21a2
求导得
V˙(e,a)=ee˙+aa˙=e(x˙d−ax2−u)−aa^˙
所以可以令 u=x˙d−a^x2+ke,带入之后得
V˙(e,a)=−ke2−a(ex2+a^˙)−ke2:ND−a(ex2+a^˙):未知
要保证其负定,但是不能保证第二项负定,但是可以令第二项为 0
−a(ex2+a^˙)=0⇓a^˙=−ex2V˙(e,a)=−ke2:NSD
引入一个引理
1◯ V≥02◯ g(t)≥0 V˙≤−g(t)3◯ g˙(t)∈L∞有界→g(t)连续⇓t→∞lim g(t)=0
可以用于验证上式
1◯ V≥02◯ V=−ke2≤−(ke2)=−g(t)g(t)=ke2≥03◯ g˙(t)=2kee˙有界⇓t→∞lim g(t)=0⇓e→0
由于 a^˙=−ex2⇒a^=−∫0tex2dτ ,可得
u=x˙d+x2∫0tex2dτ+ke
例子
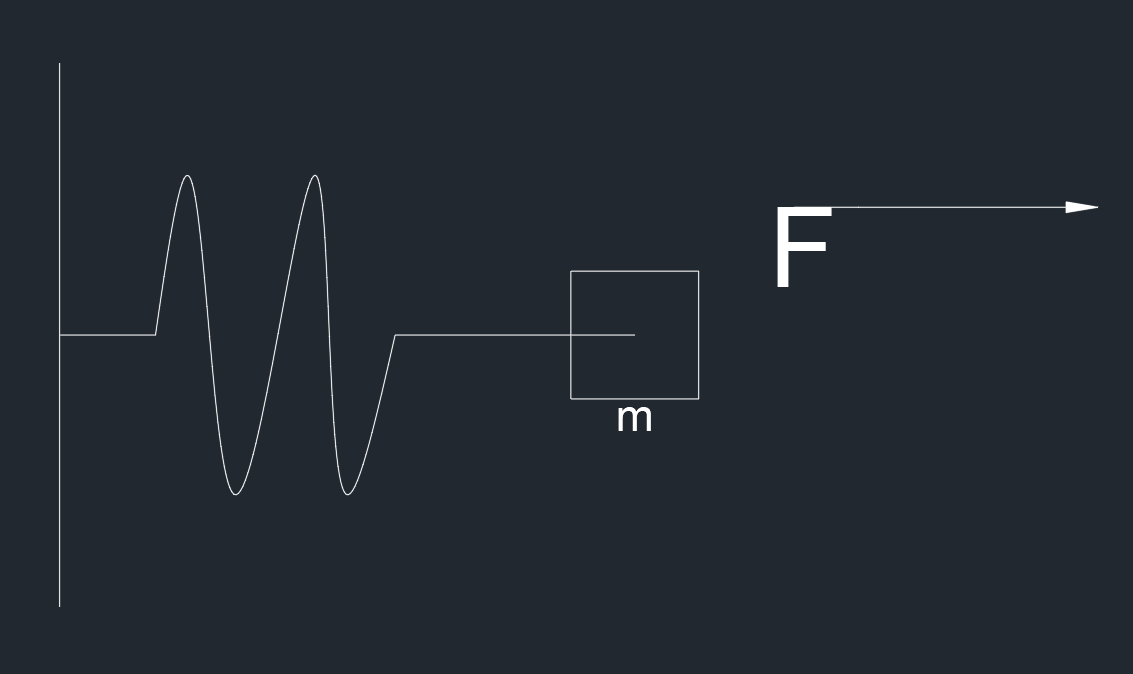
对于一个非线性弹簧滑块的系统,假设弹簧的力的与拉伸长度的关系为 F=αx3,其中 α 是一个未知数,可以列出该系统的状态方程为
mx¨+αx3=F
系统的输入为 F,滑块位移为 x,质量为 m
规定滑块的目标轨迹为 x1d ,令
x1=xx2=x˙
所以得到
x˙1=x2 1◯x˙2=−mαx13+mu 2◯
所以可以通过控制输入来控制 x˙2 进而控制 x2,从而控制 x1
引入误差 e
e=x1d−x1 3◯
从而目标变为 e→0
求导得到
e˙=x˙1d−x˙1=x˙1d−x2 4◯
可以找到一个李雅普诺夫函数 V(e) 使之渐进稳定,从而实现目标,设
V1(e)=21e2 5◯
V1 是一个正定的函数,求导得到
V˙1=e(x˙1d−x2) 6◯⇓x˙1d−x2=−k1eV˙1=−k1e2:ND
根据上述期望,可以设置x2 的期望值
x2d=x˙1d+k1e 7◯
所以目标变为 x2→x2d,令
δ=x2d−x2 8◯
将 8 带入到 6 中,得到
V˙1=e(x˙1d−(x2d−δ))
带入 7 式
V˙1=−k1e2+eδ 9◯
由于 δ˙=x˙2d−x˙2,带入 2 式和 7 式,得
δ˙=x¨1d+k1e˙−(−mαx13+mu)
带入 4 式
δ˙=x¨1d+k1(x1d−x2)+mαx13−mu 10◯
此时就需要 δ→0,e→0,需要找到新的李雅普诺夫函数 V(e,δ) 使之满足渐进稳定的条件了
V2=V1+21δ2:PD
对上式求导得到
V˙2=V˙1+δδ˙=−k1e2+eδ+δδ˙=−k1e2+δ(e+δ˙)
为使之负定,可以设计使 e+δ˙=−k2δ,带入 10 式得
e+x¨1d+k1(x1d−x2)+mαx13−mu=−k2δ
最终得到
u=me+mx¨1d+mk1(x˙1d−x2)+αx13+mk2δ 11◯
由于上述中 α 未知,所以引入一个预测值 α^ 和预测差值 α=α−α^→0
设定一个新的李雅普诺夫方程
V3=21e2+21δ2+21α2:PD
求导得到
V˙3=ee˙+δδ˙+αα˙
并且有
u=me+mx¨1d+mk1(x˙1d−x2)+α^x13+mk2δ 11◯
带入其中得到
V˙3=−k1e2−k2δ2+α(α^˙+mδx13)
已知前两项为负定,不能保证第三项为负定,所以可以使第三项为 0
α^˙=−mδx13⇓α^=−∫0tmδx13dt
则求出
u=me+mx¨1d+mk1(x˙1d−x2)−x13∫0tmδx13dt+mk2δ 11◯