对于一个非线性系统

x˙=f(x,u)\dot{x}=f(x,u)

假设 u 是 x 的函数

u=ϕ(x)u=\phi (x)

所以得到系统状态图

1
2
3
graph LR
A((u))-->B[f]-->C((x))
C-->D[Φ]-->A

反馈线性化

就是将传递函数 f(x,u)f(x,u) 中的非线性部分通过调整 ϕ(x)\phi (x) 来抵消，最终得到的是一个线性的关系

例子

x˙=f(x,u)=ax2+u\dot{x}=f(x,u)=ax^2+u

可以使得 u=ϕ(x)=−ax2−xu=\phi(x)=-ax^2-x，其中 −ax2-ax^2 用于抵消系统的非线性量，而 −x-x 用于将系统保持平稳，得到

x˙=−x↓x=e−t\dot{x}=-x\\\\ \downarrow\\\\ x=e^{-t}

当 t→∞t→\infty 时， x→0x→0

李雅普诺夫直接办法

需要选取李雅普诺夫函数来判断

例子

x˙=f(x,u)=x2−x3+u\dot{x}=f(x,u)=x^2-x^3+u

选定

V=12x2V=\frac{1}{2}x^2

由于

V(0)=0V(x)>0  x≠0V˙=x3−x4+xuV(0)=0\\\\ V(x)>0~~x\not=0\\\\ \dot{V}=x^3-x^4+xu

所以就需要设计 u 使 V˙\dot{V} 负定

已知

x3:非负定−x4:负定x^3:\text{非负定}\\\\ -x^4:\text{负定}

所以就需要选定 u 来消除 x3x^3

可以选择 u=−x2−xu=-x^2-x，消除非负定项

最终得到

x˙=−x3−x\dot{x}=-x^3-x

根据仿真的结果，可以看出，设计 uu 时一定要慎重考虑能耗和收敛速度的平衡关系

反步法

对于一个假定的系统

x˙1=f1=x12+x2x2˙=f2=x1+u\dot{x}_1=f_1=x_1^2+x_2\\\\ \dot{x_2}=f_2=x_1+u

由于控制输入并不能直接作用到目标 x1x_1 上，所以控制时就需要控制 u→x˙2→x2→x˙1→x1u\rightarrow\dot{x}_2→x_2→\dot{x}_1→x_1，但是在设计时需要反过来设计，使之不断地满足李雅普诺夫的渐近稳定条件

步骤

  1. 设计一个 x2→x2dx_2\rightarrow x_{2d} 使得 x1→x1dx_1→x_{1d}

    引入一个误差 e=x1d−x1e=x_{1d}-x_1，并且使 e→0e→0

    需要设计一个李雅普诺夫函数 V1(e)=12e2V_1(e)=\frac{1}{2}e^2，是个正定的函数，要想满足李雅普诺夫渐进稳定的条件，就保证导数负定就可以了

    要使 V˙1(e)=ee˙\dot{V}_1(e)=e\dot e 负定，可以使 V˙1(e)=−k1e2\dot{V}_1(e)=-k_1e^2，也就是

    e˙=x˙1d−x˙1=x˙1d−(x12+x2)=−k1e\dot{e}=\dot{x}_{1d}-\dot{x}_1=\dot{x}_{1d}-(x_1^2+x_2)=-k_1e

    根据上述假定的系统，要使上一步实现，就需要设定 x2dx_{2d}，使该系统有一个这样的表现

    x2d=k1e+x˙1d−x12x_{2d}=k_1e+\dot{x}_{1d}-x_1^2

  2. 设计 u 使得 x2→x2dx_2→x_{2d}

    引入一个误差 δ=x2d−x2\delta=x_{2d}-x_2，并且使 δ→0\delta→0，带入到 V˙1\dot{V}_1 中得到

    V˙1=−k1e2\dot{V}_1=-k_1e^2

    此时设计一个李雅普诺夫函数 V2(e,δ)=V1(e)+12δ2V_2(e,\delta)=V_1(e)+\frac{1}{2}\delta^2，可知它是一个正定的函数，要想满足李雅普诺夫渐进稳定的条件，就保证导数负定就可以了，其中 x2=x2d−δx_2=x_{2d}-\delta

    V˙2=ee˙+δδ˙=e(x˙1d−x12−(k1e+x˙1d−x12−δ))+δδ˙=−k1e2+eδ+δδ˙↓V˙2=−k1e2+δ(e+δ˙)\dot{V}_2=e\dot{e}+\delta\dot{\delta}=e(\dot{x}_{1d}-x_1^2-(k_1e+\dot{x}_{1d}-x_1^2-\delta))+\delta\dot\delta=-k_1e^2+e\delta+\delta\dot\delta\\\\ \downarrow\\\\ \dot{V}_2=-k_1e^2+\delta(e+\dot\delta)

    所以要使之负定，就需要保证 e+δ˙=−k2δe+\dot\delta=-k_2\delta，带入之后得到

    e+(k1e˙+x¨1d−2x1(x12+x2)−x1−u)=−k2(k1e+x˙1d−x12−x2)e+(k_1\dot{e}+\ddot{x}_{1d}-2x_1(x_1^2+x_2)-x_1-u)=-k_2(k_1e+\dot{x}_{1d}-x_1^2-x_2)

    最终得到

    u=e+k1e˙+x¨1d−2x1(x12+x2)−x1+k2(k1e+x˙1d−x12−x2)u=e+k_1\dot{e}+\ddot{x}_{1d}-2x_1(x_1^2+x_2)-x_1+k_2(k_1e+\dot{x}_{1d}-x_1^2-x_2)

一个反步法控制非线性系统的例子

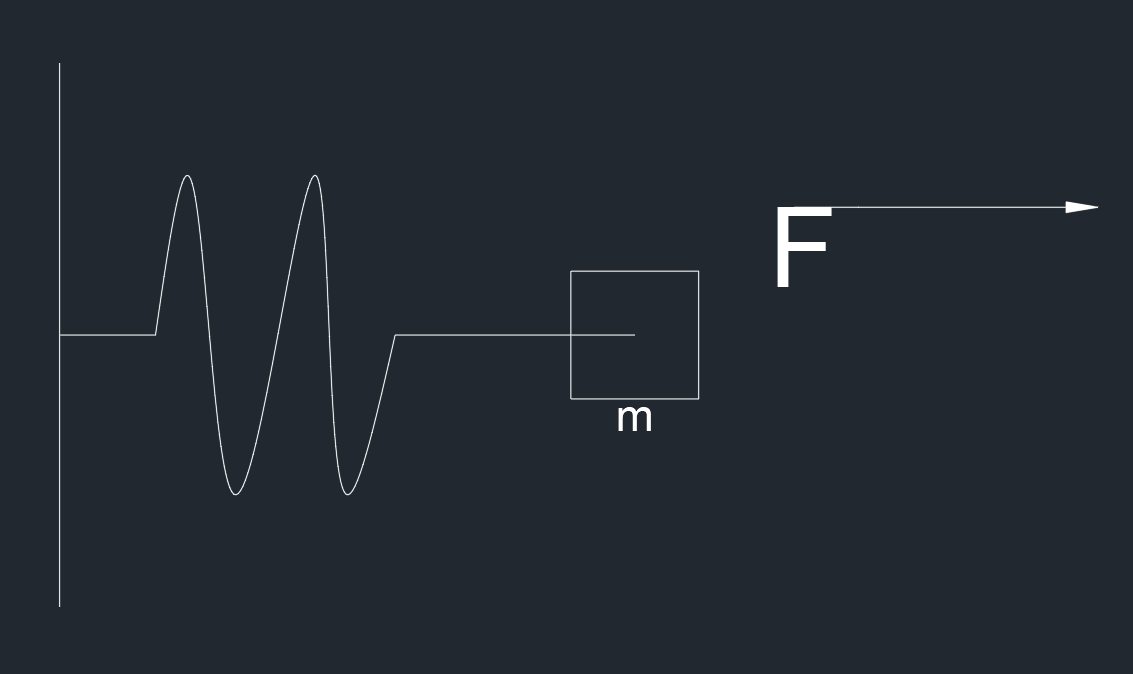
1708437413726.png

对于一个非线性弹簧滑块的系统，假设弹簧的力的与拉伸长度的关系为 F=αx3F=\alpha x^3

所以该系统的状态方程为

mx¨+αx3=Fm\ddot{x}+\alpha x^3=F

系统的输入为 FF，滑块位移为 xx，质量为 mm

规定滑块的目标轨迹为 x1dx_{1d}

令

x1=xx2=x˙x_1=x\\x_2=\dot{x}

所以得到

x˙1=x2  1◯x˙2=−αmx13+um  2◯\dot{x}_1=x_2~~\text{\textcircled{1}}\\\\ \dot{x}_2=-\frac{\alpha}{m}x_1^3+\frac{u}{m}~~\text{\textcircled{2}}

所以可以通过控制输入来控制 x˙2\dot{x}_2 进而控制 x2x_2，从而控制 x1x_1

引入误差 ee

e=x1d−x1  3◯e=x_{1d}-x_1~~\text{\textcircled{3}}

从而目标变为 e→0e→0

求导得到

e˙=x˙1d−x˙1=x˙1d−x2  4◯\dot{e}=\dot{x}_{1d}-\dot{x}_1=\dot{x}_{1d}-x_2~~\text{\textcircled{4}}

可以找到一个李雅普诺夫函数 V(e)V(e) 使之渐进稳定，从而实现目标，设

V1(e)=12e2  5◯V_1(e)=\frac{1}{2}e^2~~\text{\textcircled{5}}

V1V_1 是一个正定的函数，求导得到

V˙1=e(x˙1d−x2)  6◯⇓x˙1d−x2=−k1eV˙1=−k1e2:ND\dot{V}_1=e(\dot{x}_{1d}-x_2)~~\text{\textcircled{6}}\\\\ \Downarrow\\\\ \dot{x}_{1d}-x_2=-k_1e\\\\ \dot{V}_1=-k_1e^2:ND

根据上述期望，可以设置x2x_2 的期望值

x2d=x˙1d+k1e  7◯x_{2d}=\dot{x}_{1d}+k_1e~~\text{\textcircled{7}}

所以目标变为 x2→x2dx_2→x_{2d}，令

δ=x2d−x2  8◯\delta=x_{2d}-x_2~~\text{\textcircled{8}}

将 8 带入到 6 中，得到

V˙1=e(x˙1d−(x2d−δ))\dot{V}_1=e(\dot{x}_{1d}-(x_{2d}-\delta))

带入 7 式

V˙1=−k1e2+eδ  9◯\dot{V}_1=-k_1e^2+e\delta~~\text{\textcircled{9}}

由于 δ˙=x˙2d−x˙2\dot{\delta}=\dot{x}_{2d}-\dot{x}_2，带入 2 式和 7 式，得

δ˙=x¨1d+k1e˙−(−αmx13+um)\dot{\delta}=\ddot{x}_{1d}+k_1\dot{e}-(-\frac{\alpha}{m}x_1^3+\frac{u}{m})

带入 4 式

δ˙=x¨1d+k1(x1d−x2)+αmx13−um  10◯\dot{\delta}=\ddot{x}_{1d}+k_1(x_{1d}-x_2)+\frac{\alpha}{m}x_1^3-\frac{u}{m}~~\text{\textcircled{10}}

此时就需要 δ→0,e→0\delta→0,e→0，需要找到新的李雅普诺夫函数 V(e,δ)V(e,\delta) 使之满足渐进稳定的条件了

V2=V1+12δ2:PDV_2=V_1+\frac{1}{2}\delta^2:PD

对上式求导得到

V˙2=V˙1+δδ˙=−k1e2+eδ+δδ˙=−k1e2+δ(e+δ˙)\dot{V}_2=\dot{V}_1+\delta\dot\delta=-k_1e^2+e\delta+\delta\dot\delta=-k_1e^2+\delta(e+\dot\delta)

为使之负定，可以设计使 e+δ˙=−k2δe+\dot\delta=-k_2\delta，带入 10 式得

e+x¨1d+k1(x1d−x2)+αmx13−um=−k2δe+\ddot{x}_{1d}+k_1(x_{1d}-x_2)+\frac{\alpha}{m}x_1^3-\frac{u}{m}=-k_2\delta

最终得到

u=me+mx¨1d+mk1(x˙1d−x2)+αx13+mk2δ  11◯u=me+m\ddot{x}_{1d}+mk_1(\dot{x}_{1d}-x_2)+\alpha x_1^3+mk_2\delta~~\text{\textcircled{11}}

检验

将 8 式带入 4 式

e˙=x˙1d−(x2d−δ)=−k1e+δ\dot{e}=\dot{x}_{1d}-(x_{2d}-\delta)=-k_1e+\delta

将 11 式带入 10 式

δ˙=−e−k2δ\dot{\delta}=-e-k_2\delta

所以得到一个线性关系的系统

[e˙δ˙]=[−k11−1−k2][eδ]\begin{bmatrix}\dot{e}\\\dot{\delta}\end{bmatrix}=\begin{bmatrix}-k_1&1\\-1&-k_2\end{bmatrix}\begin{bmatrix}e\\\delta\end{bmatrix}

可以分析一下系数矩阵的特征值

λ1+λ2=−k1−k2<0λ1λ2=k1k2+1>0↓k1,k2<0\lambda_1+\lambda_2=-k_1-k_2 < 0\\\\ \lambda_1\lambda_2=k_1k_2+1 > 0\\\\ \downarrow\\\\ k_1,k_2<0

由于平衡点在零点，而且特征值均小于 0 ，是一个渐近稳定的系统