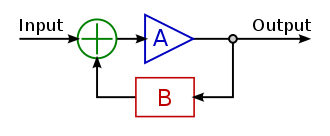
系统的可观测性
对于一个开环系统
X˙=AXy=CX
可以得到系统的状态转移方程
X=eAtX(0)
根据状态方程的解,可以知道
y=CX=CeAtX(0)
根据矩阵质数定义的状态转移矩阵有
eAt=I+At+2!1A2t2+...
取前 n 项
eAt=I+At+2!1A2t2+...+(n−1)!1An−1tn−1
带入到上面 y 的式子中
y=(CI+CAt+...+(n−1)!1CAn−1tn−1)X(0)=[It...(n−1)!1tn−1]⎣⎢⎢⎢⎡CCA…CAn−1⎦⎥⎥⎥⎤X(0)
这是一个非齐次线性方程组,要从上面的式子中唯一的解出 n 阶初始状态 x(0) 的充要条件就是下面这个矩阵为满秩。实际的意义就是保证从任意状态来说都能推导出一个唯一的初始状态
定义一个矩阵 O
O=⎣⎢⎢⎢⎡CCA…CAn−1⎦⎥⎥⎥⎤
当 Rank(O)=n 就称该系统是可观测的
观测器原理
对于系统的状态,一般都是可以直接测定的,但是有些情况,系统的状态不能够直接测定,所以要根据系统的输入和输出来估计系统的状态
对于一个系统
X˙=AX+Buy=CX+Du
设定 X^ 为系统状态的估计值, y^ 为输出的估计值
X^˙=AX^+Bu+L(y−y^)y^=CX^+Du
两式合并得
X^˙=(A−LC)X^+(B−LD)u+Ly
这就是观测器形式
可以得到
X˙−X^˙=AX+Bu−((A−LC)X^+(B−LD)u+Ly)⇓X˙−X^˙=(A−LC)X−(A−LC)X^=(A−LC)(X−X^)
此时,令
ex=X−X^
是估计值与实际值之间的误差
由于我们的目标肯定是使得实际值与估计值是一致的,所以误差值的期望是变小的,也就是 ex→0
所以根据上式可以得到一个这样的式子
ex˙=(A−LC)ex
所以就需要 A−LC 的特征值小于 0 ,才能使得该误差值逐渐趋近于 0
所以需要建立一个新的反馈系统使得 ex→0
所以,令
L=[l1l2]
带入之后选取适当的数值可以使得系统稳定
例子
一个倒立摆模型
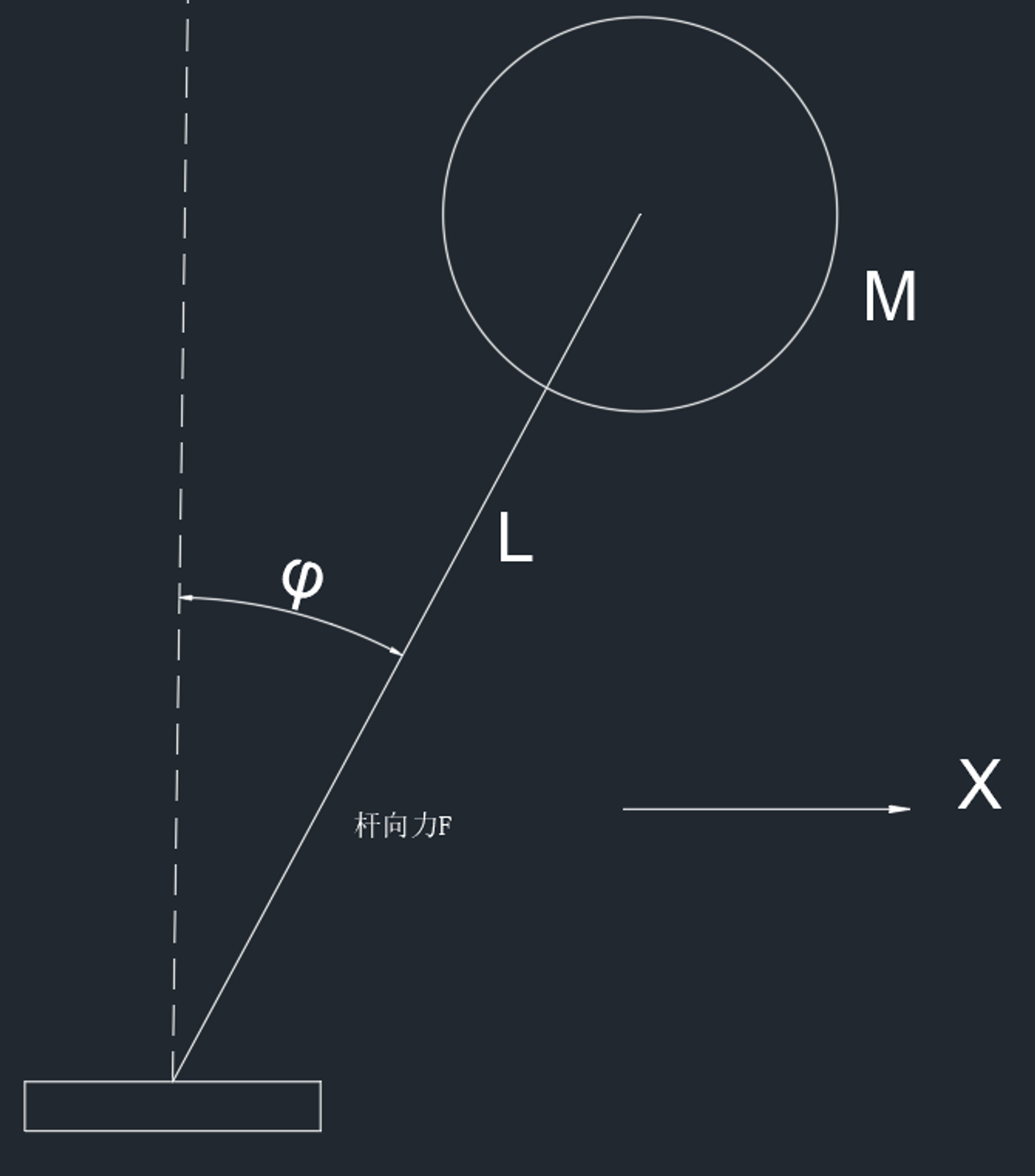
建立系统状态空间方程,令
X=[x1x2]x1=ϕx2=ϕ˙(不可测)u=L1x¨block
则从上式可以得到状态空间方程
X˙=[0Lg10]X+[0−1]uy=[10]X+[0]u
可以得到
A−LC=[0Lg10]−[l1l2][10]=[−l1Lg−l210]
可以假设
g=10 N/m2L=1 m
带入后得到
A−LC=[−l110−l210]
求其特征方程为
∣λI−(A−LC)∣=0↓λ2+l1λ+l2−10=0
所以,令该特征方程的两个根都为 -1 ,可以得到
l1=2l2=11
所以带入到估计值的方程中可以得到
X^˙=(A−LC)X^+(B−LD)u+Ly⇓X^˙=[−2−110]X^+[0−1]u+[211]y