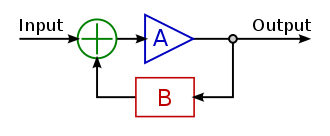
系统控制

对于一个开环控制器来说

X˙=AX\dot{X}=AX

这里的 AA 的特征值 λ\lambda 决定系统的表现，稳定性

当引入一个输入量时，控制器变为

X˙=AX+Bu\dot{X}=AX+Bu

其中由于 uu 是 XX 的函数，所以系统形成了一个闭环控制

对于线性控制器来说，输入 uu 满足

u=−KXu=-KX

代入到控制器中可以得到

X˙=AX−BKX=(A−BK)X\dot{X}=AX-BKX=(A-BK)X

可以选择 KK 的数值来使得 XX 前的系数的特征值 λi\lambda_i 处于一个期望的位置上，一般来说，需要保证其特征值均 ≤0≤0 才能使得系统稳定

选取 λi\lambda_i 的原则

  • 如果选取 λ\lambda 为虚数，那么一定会有共轭解存在，将一定会引入一个反复的振动
  • λ\lambda 决定收敛的速度，最后的解的形式会变为 c1eλ1+c2eλ2+...c_1e^{\lambda_1}+c_2e^{\lambda_2}+...
  • 考虑输入 uu，有些控制理论中会引入代价函数 J=∫0∞(XTQX+UTRU)dtJ=\int_0^{\infty}(X^TQX+U^TRU)dt ，用于调节参数平衡 u 与系统稳定的关系

控制器设计之前一定要判断一下系统的可控性，一般来说 先可控，再稳定

一个小栗子

对于一阶倒立摆模型，下面的小块也能移动

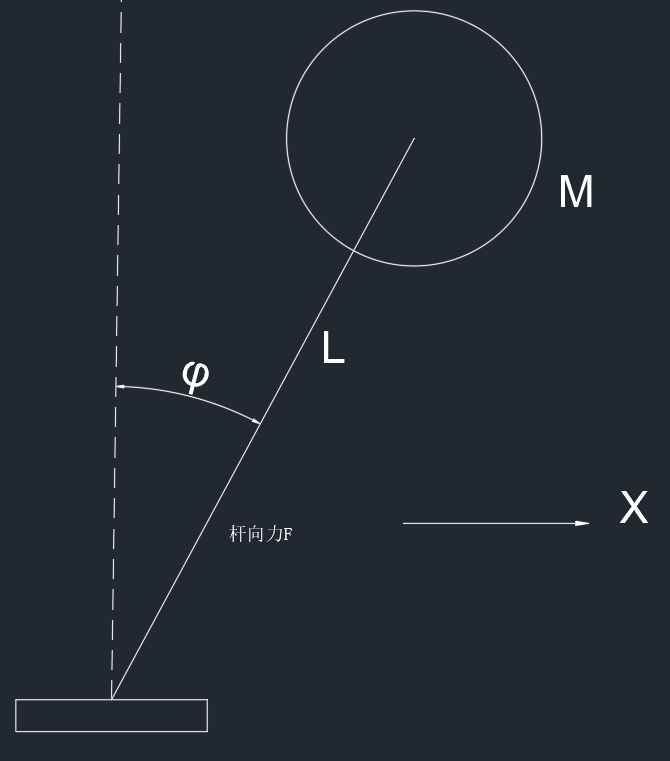
1708349286931.png

当小球在运动中的运动学方程（初始位置为竖直点）

xball=Lsin(ϕ)+xblock→xball=Lϕ+xblockyball=L(1−cos(ϕ))=0x_{ball}=Lsin(\phi)+x_{block}\rightarrow x_{ball}=L\phi+x_{block}\\y_{ball}=L(1-cos(\phi))=0

小球的动力学方程

Fx=mx¨ball=Fsin(ϕ)=Fϕ=MLϕ¨+mx¨blockFy=Fcos(ϕ)=F=MgF_x=m\ddot{x}_{ball}=Fsin(\phi)=F\phi=ML\ddot{\phi}+m\ddot{x}_{block}\\F_y=Fcos(\phi)=F=Mg

动力学方程化简得到

Mgϕ=MLϕ¨+Mx¨block⇓ϕ¨−gLϕ+1Lx¨block=0Mg\phi=ML\ddot{\phi}+M\ddot{x}_{block}\\\Downarrow\\\ddot{\phi}-\frac{g}{L}\phi+\frac{1}{L}\ddot{x}_{block}=0

建立系统状态空间方程，令

X=[x1x2]x1=ϕx2=ϕ˙u=1Lx¨blockX=\begin{bmatrix}x_1\\x_2\end{bmatrix}\\x_1=\phi\\x_2=\dot{\phi}\\u=\frac{1}{L}\ddot{x}_{block}

则从上式可以得到状态空间方程

X˙=[01gL0]X+[0−1]uy=[10]X+[0]u\dot{X}=\begin{bmatrix}0&1\\\frac{g}{L}&0\end{bmatrix}X+\begin{bmatrix}0\\-1\end{bmatrix}u\\y=\begin{bmatrix}1&0\end{bmatrix}X+[0]u

  • 对于开环系统，也就是没有输入 u

    A=[01gL0]A=\begin{bmatrix}0&1\\\frac{g}{L}&0\end{bmatrix}

    特征值中有一个大于 0 的特征值，不稳定

  • 对于闭环系统

    系统的可控性，由系统的可控性中可知

    Co=[BAB]=[0−1−10]Rank(Co)=2Co=\begin{bmatrix}B&AB\end{bmatrix}=\begin{bmatrix}0&-1\\-1&0\end{bmatrix}\\Rank(Co)=2

    所以系统可控，令

    u=−[k1k2]Xu=-\begin{bmatrix}k_1&k_2\end{bmatrix}X

    带入之后得到

    X˙=[01gL+k1k2]X=AdX\dot{X}=\begin{bmatrix}0&1\\\frac{g}{L}+k_1&k_2\end{bmatrix}X=A_dX

    求系数矩阵的特征根

    ∣λI−Ad∣=0⇓λ2−k2λ−gL−k1=0|\lambda I-A_d|=0\\\Downarrow\\\lambda^2-k_2\lambda-\frac{g}{L}-k_1=0

    为了使得系统稳定，所以一般使其特征根位于负半轴上，所以可以将该式子定义为

    λ2−k2λ−gL−k1=0=λ2+2λ+1\lambda^2-k_2\lambda-\frac{g}{L}-k_1=0=\lambda^2+2\lambda+1

    得到

    k1=−1−gLk2=−2k_1=-1-\frac{g}{L}\\k_2=-2

    带入之后得到

    u=[1+gL2]Xu=\begin{bmatrix}1+\frac{g}{L}&2\end{bmatrix}X

线性控制器——状态跟踪

对于上面所设计的控制器，如果想要使系统状态稳定再某一个位置时，就需要使用状态跟踪了

所以引入一个期望值，这里不对 x2x_2 进行跟踪

x1dx_{1d}

令

e1=x1d−x1E=[e1x2]e_1=x_{1d}-x_1\\\\E=\begin{bmatrix}e_1\\x_2\end{bmatrix}

一般来说，系统的期望值是不变的，所以可以得到

e1˙=−x˙1\dot{e_1}=-\dot{x}_1

所以可以得到，这里的 a11a_{11} 是矩阵 A 中的一个元素

E˙=AE+Bu−[0a11]x1d\dot{E}=AE+Bu-\begin{bmatrix}0\\a_{11}\end{bmatrix}x_{1d}

可以设计控制器，目的是稳定系统和调整平衡点

u=−KE−Bd−1GXdu=-KE-B_d^{-1}GX_d

带入得到

E˙=(Ad−BdK)E\dot{E}=(A_d-B_dK)E

所以需要选择合适的 KK 使系统稳定

还是上面那个倒立摆的例子

对于上面所设计的控制器，如果想要使系统状态稳定再某一个位置时，就需要使用状态跟踪了

所以引入一个期望值，这里不对 x2x_2 进行跟踪

x1dx_{1d}

令

e1=x1d−x1E=[e1x2]e_1=x_{1d}-x_1\\\\E=\begin{bmatrix}e_1\\x_2\end{bmatrix}

一般来说，系统的期望值是不变的，所以可以得到

e1˙=−x˙1\dot{e_1}=-\dot{x}_1

对于上面的系统

A=[01gL0]B=[0−1]A=\begin{bmatrix}0&1\\\frac{g}{L}&0\end{bmatrix}\\B=\begin{bmatrix}0\\-1\end{bmatrix}

带入得到

E˙=[0−1−gL0]E+[0−1]u+[0gL]x1d\dot{E}=\begin{bmatrix}0&-1\\-\frac{g}{L}&0\end{bmatrix}E+\begin{bmatrix}0\\-1\end{bmatrix}u+\begin{bmatrix}0\\\frac{g}{L}\end{bmatrix}x_{1d}

所以可以设计

u=−KE+gLx1du=-KE+\frac{g}{L}x_{1d}

带入之后得到

A−BK=[01−gL+k1k2]A-BK=\begin{bmatrix}0&1\\-\frac{g}{L}+k_1&k_2\end{bmatrix}

求得特征方程为

λ2−k2λ+k1−gL=0\lambda^2-k_2\lambda+k_1-\frac{g}{L}=0

令

λ2−k2λ−gL+k1=0=λ2+2λ+1\lambda^2-k_2\lambda-\frac{g}{L}+k_1=0=\lambda^2+2\lambda+1

得到

k2=−2k1=1+gLk_2=-2\\k_1=1+\frac{g}{L}

也就是

u=[−1−gL2]E+gLx1d=−x1d+(1+gL)x1+2x2u=\begin{bmatrix}-1-\frac{g}{L}&2\end{bmatrix}E+\frac{g}{L}x_{1d}=-x_{1d}+(1+\frac{g}{L})x_1+2x_2