状态空间

对于一个系统的状态空间方程，可以使用 laplace 变换来得到系统的运行状态方程

状态空间方程——一个包含输入，输出，状态变量的集合的一阶微分方程，但是对于高阶的系统，可以选择合适的状态量来消除高阶的系数

根据下式求出的状态空间方程中，对于矩阵 A 的特征值是决定系统极点的位置，可能会决定系统的稳定性

状态空间方程的解

过程不再写了，直接结论

X(t)=eA(t−t0)X(t0)+∫t0teA(t−τ)Bu(τ)dτX(t)=e^{A(t-t_0)}X(t_0)+\int_{t_0}^t{e^{A(t-\tau)}Bu(\tau)}d\tau

其中 eA(t−t0)e^{A(t-t_0)} 是状态转移矩阵，表示系统状态转移变化的规律，是一个实时变化的矩阵，A 矩阵对其有着重要的作用，当 A 的特征值小于0时， X(t)X(t) 是不断趋近于 0 的，是系统稳定性分析的一个重要方式，但是 A 矩阵的特征值中含有虚数就表示该系统是有震荡的（根据欧拉公式，引入虚数相当于是引入了 sint 和 cost，实际上是引入了震荡），要保证系统稳定，一定要保证特征值的实部小于零

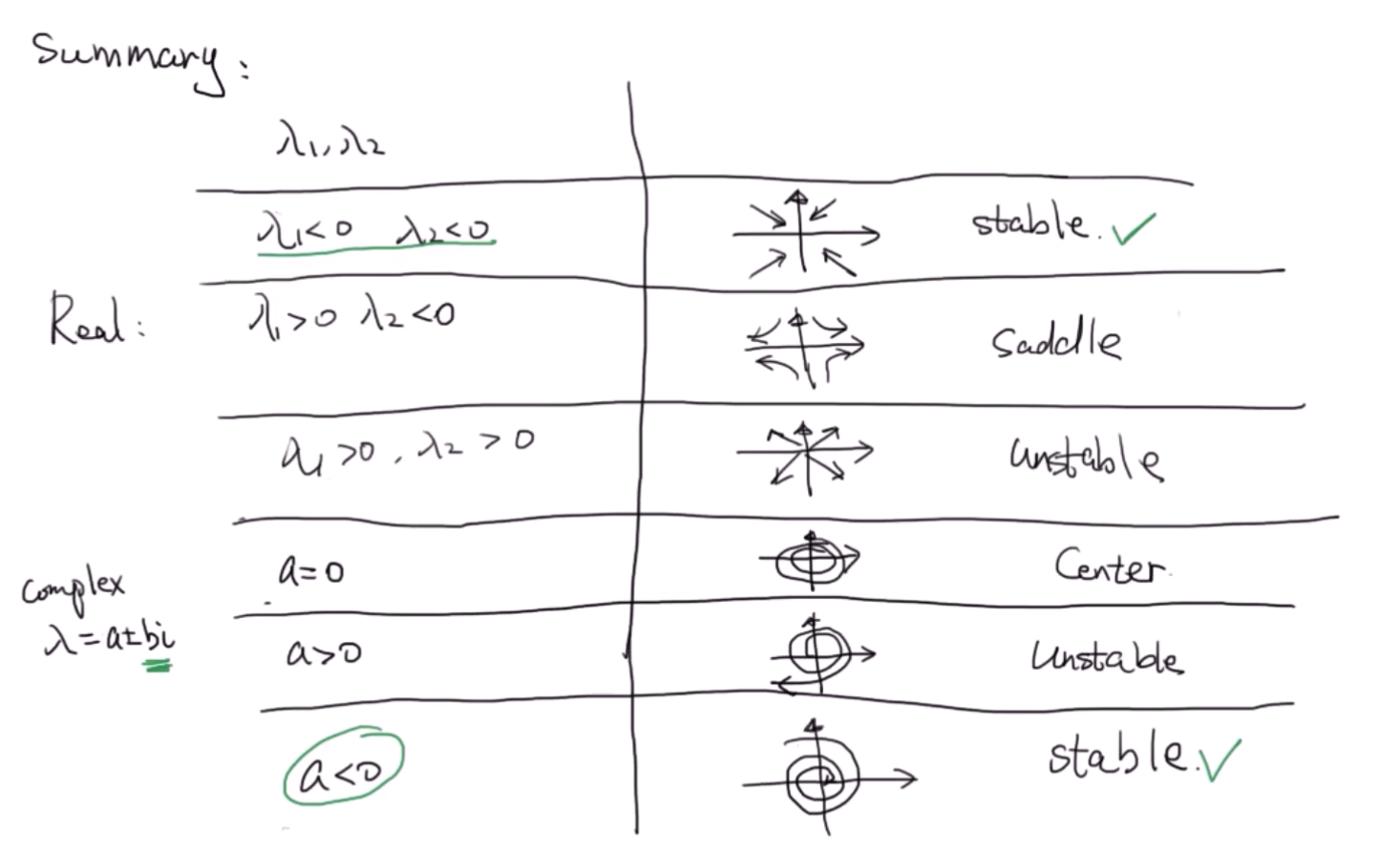
1708342322241.png

第二项是一个卷积，表示输入与输出之间的动态变化的关系

传递函数→状态空间方程

一阶系统

假设传递函数为

G(s)=Y(s)U(s)=a0b0s+b1G(s)=\frac{Y(s)}{U(s)}=\frac{a_0}{b_0s+b_1}

可以写作

Y(s)(b0s+b1)=a0U(s)Y(s)(b_0s+b_1)=a_0U(s)

即

b0y˙+b1y=a0ub_0\dot{y}+b_1y=a_0u

则可设

x1=yx_1=y

则有

x1˙=−b1b0x1+a0b0uy=x1\dot{x_1}=-\frac{b_1}{b_0}x_1+\frac{a_0}{b_0}u\\\\ y=x_1

得到状态方程

A=−b1b0B=a0b0C=1A=-\frac{b_1}{b_0}\\\\ B=\frac{a_0}{b_0}\\\\ C=1

二阶系统

设传递函数为

G(s)=Y(s)U(s)=a0s+a1b0s2+b1s+b2G(s)=\frac{Y(s)}{U(s)}=\frac{a_0s+a_1}{b_0s^2+b_1s+b_2}

写作

Y(s)(b0s2+b1s+b2)=(a0s+a1)U(s)Y(s)(b_0s^2+b_1s+b_2)=(a_0s+a_1)U(s)

b0y¨+b1y˙+b2y=a0x˙+a1xb_0\ddot{y}+b_1\dot{y}+b_2y=a_0\dot{x}+a_1{x}

令

b0y1¨+b1y1˙+b2y1=uy=a0x1˙+a1x1b_0\ddot{y_1}+b_1\dot{y_1}+b_2y_1=u\\\\ y=a_0\dot{x_1}+a_1x_1

{x1=y1x2=y1˙\left\{\begin{aligned}&x_1=y_1\\&x_2=\dot{y_1}\end{aligned}\right.

{[x1˙x2˙]=[01−b2b0−b1b0][x1x2]+[01b0]uy=[a1a0][x1x2]\left\{\begin{aligned}&\begin{bmatrix}\dot{x_1}\\\dot{x_2}\end{bmatrix}=\begin{bmatrix}0&1\\-\frac{b_2}{b_0}&-\frac{b_1}{b_0}\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}+\begin{bmatrix}0\\\frac{1}{b_0}\end{bmatrix}u\\&y=\begin{bmatrix}a_1&a_0\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}\end{aligned}\right.

则

A=[01−b2b0−b1b0]B=[01b0]C=[a1a0]A=\begin{bmatrix}0&1\\-\frac{b_2}{b_0}&-\frac{b_1}{b_0}\end{bmatrix}\\\\ B=\begin{bmatrix}0\\\frac{1}{b_0}\end{bmatrix}\\\\ C=\begin{bmatrix}a_1&a_0\end{bmatrix}

高阶系统

G(s)=Y(s)X(s)=∑i=0N−1aisi∑i=0NbisiG(s)=\frac{Y(s)}{X(s)}=\frac{\sum_{i=0}^{N-1}a_is^i}{\sum_{i=0}^{N}b_is^i}

则

{X˙=AX+BUY=CX\left\{\begin{aligned}&\dot{X}=AX+BU\\&Y=CX\end{aligned}\right.

其中

A=[010000100001−b0bN−b1bN−b2bN−bN−1bN]B=[001bN]C=[a0a1a2aN−1]A=\begin{bmatrix}0&1&0&&0\\0&0&1&&0\\\\0&0&0&&1\\-\frac{b_0}{b_N}&-\frac{b_1}{b_N}&-\frac{b_2}{b_N}&&-\frac{b_{N-1}}{b_N}\end{bmatrix}\\\\ B=\begin{bmatrix}0\\0\\\\\frac{1}{b_N}\end{bmatrix}\\\\ C=\begin{bmatrix}a_0&a_1&a_2&&a_{N-1}\end{bmatrix}

状态空间方程→传递函数

对于一个状态空间方程

{X˙=AX+BUY=CX+Du\left\{\begin{aligned}&\dot{X}=AX+BU\\&Y=CX+Du\end{aligned}\right.

对方程两侧进行 laplace 变换，得

L(X˙)=L(AX+Bu)sX(s)=AX(s)+Bu(s)(sI−A)X(s)=Bu(s)L(\dot{X})=L(AX+Bu)\\\\ sX(s)=AX(s)+Bu(s)\\\\ (sI-A)X(s)=Bu(s)

其中 II 是单位对角阵，所以可以得出

X(s)=(SI−A)−1Bu(s)X(s)=(SI-A)^{-1}Bu(s)

对另一个式子进行 laplace 变换得到

L(Y)=L(CX+Du)Y(s)=CX(s)+Du(s)L(Y)=L(CX+Du)\\\\ Y(s)=CX(s)+Du(s)

带入得

Y(s)=(C(SI−A)−1B+D)u(s)Y(s)=(C(SI-A)^{-1}B+D)u(s)

所以得到传递函数

G(s)=C(sI−A)−1B+DG(s)=C(sI-A)^{-1}B+D

连续系统离散化

对于传递函数

x˙=Ax+Bu\dot{x}=Ax+Bu

该系统进行离散化之后可以得到

x(k+1)=A‾x(k)+B‾u(k)x(k+1)=\overline Ax(k)+\overline{B}u(k)

其中

A‾=eATB‾=∫\overline{A}=e^{AT}\\\\ \overline{B}=\int

对 eATe^{AT} 进行泰勒级数展开，得到

eAT=I+AT+12!A2T2+e^{AT}=I+AT+\frac{1}{2!}A^2T^2+

一般来说可以只取前三项