不变性原理

前言

李雅普诺夫的不变性原理（LaSalle’s Invariance Principle，也称为李雅普诺夫-拉塞尔不变性原理）是动力系统和控制理论中用于分析系统长期行为的重要工具。它是对经典李雅普诺夫稳定性理论的扩展，尤其在处理非线性系统时非常有用。

示例

对于一个简单的倒立摆

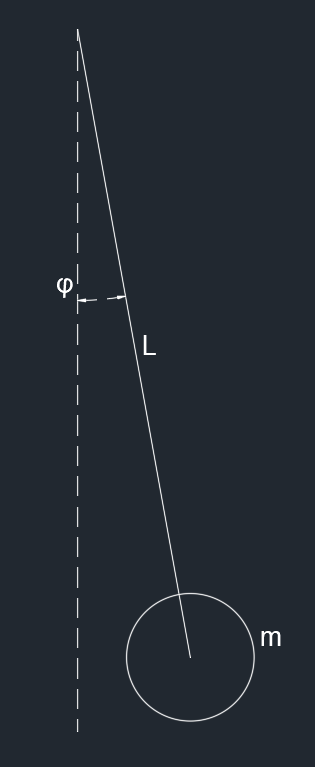
可以求出系统状态空间方程是

$L\ddot{\phi}+gsin\phi=0$

设

$x=\begin{bmatrix}x_1\\x_2\end{bmatrix}\\ x_1=\phi\\ x_2=\dot{\phi}$

求导之后可以得到

$\dot{x}_1=x_2\\ \dot{x}_2=-\frac{g}{L}sinx_1$

寻找李雅普诺夫函数，可以使用能量方程来求解

$E=K+P\\ =\frac{1}{2}mv^2+mgh=\frac{1}{2}m(L\dot{\phi})^2+mgL(1-cos\phi)$

其中 $K$ 是动能， $P$ 是势能，所以可以得到李雅普诺夫函数

$V(x)=\frac{1}{2}m(Lx_2)^2+mgL(1-cosx_1)$

开始分析，看得出来

$V(0)=0$

并且，对于任意 $x_1,x_2$，可以得到

$V(x)>0$

是满足正定条件的，对上述公式求导得到

$\dot{V}=\triangledown V f(x)=\begin{bmatrix}\frac{\partial V}{\partial x_1}&\frac{\partial V}{\partial x_2}\end{bmatrix}\begin{bmatrix}f_1\\f_2\end{bmatrix}=\begin{bmatrix}mgLsinx_1&mL^2x_2\end{bmatrix}\begin{bmatrix}x_2\\-\frac{g}{L}sinx_1\end{bmatrix}=0$

所以满足半负定

$\dot{V}=0\leq 0$

所以这个系统稳定，并且 $\dot{V}=0$ 表明这个系统能量不变

当引入阻力之后，可以得到

$mL\ddot{\phi}=-mgsin\dot{\phi}-kL\dot{\phi}\\\\ V(x)=\frac{1}{2}m(Lx_2)^2+mgL(1-cosx_1)\\\\ \dot{V}(x)=-kL^2x_2^2$

在这里出现一个很离谱的情况，也就是 $\dot{V}(x)$ 在 $\begin{bmatrix}x_1&0\end{bmatrix}$ 处总是为 0 的，这导致该函数并不是一个负定的，而是一个半负定系统。

这个系统是一个稳定系统，不是一个渐进稳定系统

动机

在上述的例子中

$mL\ddot{\phi}=-mgsin\dot{\phi}-kL\dot{\phi}\\\\ V(x)=\frac{1}{2}m(Lx_2)^2+mgL(1-cosx_1)\\\\ \dot{V}(x)=-kL^2x_2^2$

所以可以得到

$V(0)=0~:~PD\\\\ V(x)>0\\\\ \dot{V}\leq 0~:~NSD$

系统是一个稳定系统，但不是一个渐进稳定系统，根据物理学，这个系统最终会停下来，但是数学上并没有证明，所以引入不变性原理，用来扩大李雅普诺夫的判定

不变性原理

核心思想

不变性原理通过结合李雅普诺夫函数和系统动态特性，确定系统状态最终会收敛到某个特定的集合，不仅仅是稳定的平衡点

即对于一个自治的系统

$\dot{x}=f(x)$

其中 $f$ 是局部利普希茨连续的，则假设存在一个李雅普诺夫函数 $V(x)$ 满足

正定性，即 $V(x)\geq0$ ，且仅当 $x=0$ 时 $$V(x)=0$
非增性：沿系统的轨迹中有 $\dot{V}(x)\leq0$

定义集合

$S=\{x|\dot{V}(x)=0\}$

并且设 $M$ 为 $S$ 内的最大不变集，则所有有界的系统轨迹最终都会收敛到 $M$ 。不变集即系统状态一旦进入到该集合内，将永远停留在其中

结论

$V(x):PD$
$\dot{V}(x):NSD$
当且仅当 $X=0$ 时， $\dot{V}=0$

满足系统在平衡点渐进稳定

例子

对于上述的例子，已知 $V(x):PD,\dot{V}(x):NSD$

所以可以令 $\dot{V}=0$，此时 $x_2=0$。

当 $\dot{V}$ 恒为 0 时， $x_2$ 恒为 0，也就是 $\dot{x}_2$ 恒为 0

由于

$\dot{x}_2=-\frac{g}{L}sinx_1$

所以 $x_1$ 恒为 0，也就证明了只有当 $X=0$ 时， $\dot{V}=0$ ，也就是系统是渐进稳定的