前馈神经网络

前言

前馈神经网络是人工神经网络的一种，研究始于20世纪60年代。其结构由输入层、隐含层和输出层单向连接组成，信号通过有向无环图单向传播，各层神经元仅与相邻层建立连接。前馈神经网络的核心特征就是信息的单向传递，即输入数据从输入层流向隐藏层，最终到达输出层，不存在层与层之间的反向连接或循环连接。

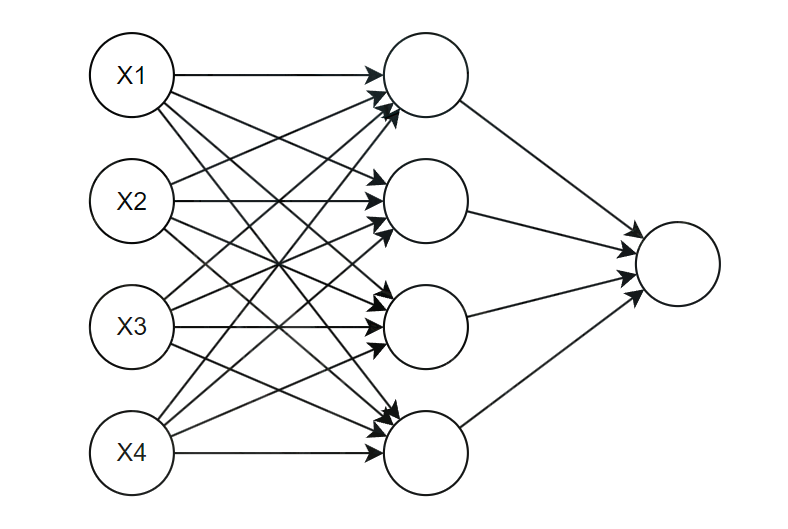
如图中所示，每个圆圈都是一个神经元，神经元是模拟生物神经元的接收-处理-输出的结构，通过接收来自于上一层的信号，每个输入对于一个可学习的权重和偏置参数，输出结果为 $z=\vec{w}\vec{x}+b$ 。之后加上激活函数，激活函数对上述的线性输出结果进行非线性变换，输出结果为 $a=f(z)$ ，这个主要是向网络中引入非线性，让网络能拟合复杂的函数模型。神经网络学习的本质就是不断调整这些权重和偏置的过程。

网络结构

输入层

输入层是网络的数据入口，接收原始的特征数据，不进行任何计算操作，神经元数量等于输入数据的特征维度。输入层的神经元只起到数据传递的作用，无激活函数

隐藏层

隐藏层是位于输入层和输出层之间的核心计算层

• 层数与神经元数量：隐藏层的层数和每层的神经元数量是 FNN 的核心超参数。
• 隐藏层的每个神经元都会接收上一层的所有神经元的输出，进行加权求和之后，再通过激活函数引入非线性变换

$$z_i=\sum_jw_{ij}x_j+b_i\\a_i=\sigma(z_i)$$

其中 $\sigma$ 是激活函数，如果没有激活函数，无论多少层隐藏层，整个网络的输出都只是输入的线性组合，无法解决非线性问题

输出层

输出层是网络的结果输出端，其神经元的数量由具体的任务确定，输出值对应着任务的预测结果，同时会根据任务类型选择不同的激活函数。

• 回归任务中的输出神经元的数量一般为 1，通常无激活函数，输出结果为连续值
• 多分类任务中输出层的数量一般等于类别数，激活函数一般用 softmax，且概率之和为 1。二分类任务中输出层神经元数量为 1，激活函数使用 sigmoid

激活函数

激活函数是神经网络能学习复杂模型的核心，如果没有激活函数，多层的神经网络就可以简化为单层线性的模型。

• 阈值函数（Threshold Function）

  • 输出为二值（0 或 1），根据输入是否超过某个阈值来决定

    $$f(x)=\left\{\begin{aligned}1&&x\geq\theta\\0&&x<\theta\end{aligned}\right.$$

• Sigmoid 函数

  • Sigmoid 函数将任意输入映射到 $(0, 1)$ 之间，常用于二分类问题

  • Sigmoid 函数的平滑性使得它在梯度下降等优化算法中表现较好

    $$f(x)=\frac{1}{1+e^{-x}}$$

• Tanh 函数（双曲正切函数）

  • Tanh 函数将输入映射到 $(-1, 1)$ 之间

  • Tanh 函数在某些情况下比 Sigmoid 表现更好，因为它关于原点对称。

    $$f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$

• ReLU 函数（Rectified Linear Unit）

  • ReLU 函数是目前深度学习中最常用的激活函数之一

  • ReLU 函数计算简单，梯度下降时收敛速度快，但在输入为负值时存在梯度消失问题

    $$f(x)=\max(0,x)$$

• Leaky ReLU

  • Leaky ReLU 是 ReLU 的改进版本，允许输入为负值时有小的梯度

  • 其中 $\alpha$ 是一个很小的常数

    $$f(x)=\left\{\begin{aligned}x&&x\geq0\\\alpha x&&x<0\end{aligned}\right.$$

• Parametric ReLU（PReLU）

  • PReLU 是 Leaky ReLU 的进一步扩展，其中的 $\alpha$ 是一个可学习的参数，数学表达式类似于 Leaky ReLU，但 $\alpha$ 在训练过程中可以调整

• Sigmoid Linear Unit（SiLU）

  $$f(x)=x\times Sigmoid(x)$$

网络层级

多层神经元按照功能分为三类层级

• 输入层：接收原始数据，不做计算
• 隐藏层：核心特征抽象层，层数越多就能学习越复杂的特征。深度学习就是拥有多个隐藏层，浅层隐藏层学习低级特征，深层隐藏层学习高级或者抽象的特征。
• 输出层：输出任务结果，具体的纬度由学习任务来决定
  • 回归任务：预测一个数值，通常有 1 个神经元，无激活函数，或者使用线性函数
  • 二分类任务：只有一个神经元，使用 Sigmoid 函数作为激活函数
  • 多分类任务：神经元数量等于类别数，使用 Softmax 作为激活函数

损失函数

深度学习的损失函数是一个至关重要的东西，不仅是衡量模型好坏的标准，也能引导模型学习方向。一个将模型的预测值和真实值映射到一个函数，这个数值就是这个模型的错误程度，之后通过优化算法来最小化这个损失值。

交叉熵损失函数

交叉熵损失函数是分类任务的标准损失函数，是衡量模型预测的概率分布与真实概率分布之间的差异

• 二分类交叉熵损失 $L=-\frac{1}{N}\sum_i^N[y_i\log(\hat{y})+(1-y_i)\log(1-\hat{y})]$ 。输出层使用 Sigmoid 激活函数，这个激活函数输出一个 0 到 1 之间的概率
• 多分类交叉熵损失 $L=-\frac{1}{N}\sum_i^Ny_i\log(\hat{y}_i)$ ，输出层使用 Softmax 激活函数，输出一个所有类别的概率分布，这些概率之和为 1。
• 平衡交叉熵损失 $L=-\frac{1}{N}\sum_i^N[\gamma y_i\log(\hat{y})+(1-\gamma)(1-y_i)\log(1-\hat{y})]$ ，就是在损失函数中添加权重因子 $\gamma\in[0,1]$ ，其中 $\frac{\gamma}{1-\gamma}=\frac{n}{m}$ ，其中正样本数量为 $n$ ，负样本数量为 $m$

交叉熵损失很适合配合 Softmax 和 Sigmoid 函数使用，在反向传播时，能传递一个很有效的梯度值

合页损失函数

在传统的 SVM 中使用，公式为 $L=\sum_i^N\max(0,1-y_i\hat{y}_i)$ ，其中 $y_i$ 是 $\plusmn1$ 的标签

使用中不如交叉熵损失使用的普遍，但是在一些特定的对比学习中会使用

Focal Loss 函数

这是深度学习中为了解决类别不平衡问题而专门设计的一个变体，例如在目标检测中图像中大部分都是背景，只有少量区域是需要检测的物体。它可以动态降低训练过程中易于区分的样本的权重，从而将中心快速聚焦在那些难以区分的样本上。

对于二分类交叉熵的损失，对于单个样本的损失函数，可以写作如下形式

$$L=\left\{\begin{aligned}&-\log(p)&&p=1\\&-\log(1-p)&&otherwise\end{aligned}\right.$$

在上述的二分类交叉熵的公式中，其中 $y$ 的取值为 1 和 -1，分别代表正样本和负样本，而预测的概率 $p=\hat{y}$ 取值范围为 $0\sim1$ ，是模型预测属于目标的概率，然后定义一个关于 $p$ 的函数。

$$p_t=\left\{\begin{aligned}&p&&y=1\\&1-p&&otherwise\end{aligned}\right.$$

结合上述二分类交叉熵的公式可以得到简化之后的公式

$$L=-\log(p_t)$$

在 focal loss 中引入了一个调制因子 $\gamma\in[0,5]$ ，用于聚焦难分的样本

$$FL=-(1-p_t)^\gamma\log(p_t)$$

这里举两个例子，当 $\gamma=5$ 时，若有两个样本都是正样本也就是 $y=1$ ，此时对两个样本的预测结果为 $p_1=0.2$ 和 $p_2=0.8$ ，此时计算两个样本的 $FL$ 和 $L$

$$L_1=-\log(0.2)\\L_2=-\log(0.8)\\FL_1=-(0.8)^5\log(0.2)\\FL_2=-(0.2)^5\log(0.8)$$

很明显可以看出 2 号样本是易于区分的样本，而 1 号样本是不易于区分的样本，两个样本在总体损失函数中所占的比例之比从 $\frac{L_1}{L_2}=3.1324$ 变成了 $\frac{FL_1}{FL_2}=3207.6$ 可以看出，不易区分的样本在整体损失函数中的比例增大了，而易于区分的样本在整体损失函数中比例减小了，这就能让损失函数更好的聚焦于不易于区分的样本上。

均方误差损失

用于回归任务，公式为 $L=\frac{1}{N}\sum_i^N(y_i-\hat{y}_i)$ ，它对异常值很敏感，会放大误差造成的影响。

平均绝对误差损失

用于回归任务，公式为 $L=\frac{1}{N}\sum_i^N\vert y_i-\hat{y}_i\vert$ ，对异常值比均方误差更稳健，但是在误差为 0 处不可导

Huber Loss

用于回归任务，结合了上述的两种损失函数的思想，误差较小时就类似于均方误差损失，而误差较大时就类似于平均绝对误差损失。

$$L=\left\{\begin{aligned}&\frac{1}{2}(y-\hat{y})^2&&\vert y-\hat{y}\vert\leq\delta\\&\delta\vert y-\hat{y}\vert-\frac{1}{2}\delta^2&&otherwise\end{aligned}\right.$$

他对异常值不敏感，如果数据中有异常值，就可以选择使用这个函数

优化器

深度学习中的优化器是至关重要的，优化器决定了模型如何基于损失函数的梯度来更新权重和偏置，直接影响到模型的收敛速度和最终性能。在使用优化器时往往会遇到很多问题，例如学习率太小导致收敛速度慢，训练时间长，而学习率太大导致模型在最优点附近震荡，甚至发散从而无法收敛。

• 批量梯度下降 SGD：每次迭代时，使用所有的训练数据来计算损失函数的梯度，然后根据这个梯度更新模型的参数

  • 理想状态下经过足够多次数的迭代，可以得到全局最优解，具有误差梯度和聚合性

  • 计算量大

    $$J(w,b)=\frac{\sum_{i=0}^n(\hat y_i-y_i)^2}{2n}\\w_{i}=w_{i-1}-\alpha\frac{\partial}{\partial w}J(w_{i-1},b_{i-1})\\b_{i}=b_{i-1}-\alpha\frac{\partial}{\partial b}J(w_{i-1},b_{i-1})\\w_0=w_{initial}\\b_0=b_{initial}$$

• 随机梯度下降：每次迭代使用一个样本来计算梯度

  • 计算效率高，随机性大，可能有利于跳出局部最优解

  • 更新过程具有较大的波动性，无法保证梯度更新的稳定性，容易受到学习率的影响

    $$J(w,b)=\frac{(\hat y_i-y_i)^2}{2}\\w_{i}=w_{i-1}-\alpha\frac{\partial}{\partial w}J(w_{i-1},b_{i-1})\\b_{i}=b_{i-1}-\alpha\frac{\partial}{\partial b}J(w_{i-1},b_{i-1})\\w_0=w_{initial}\\b_0=b_{initial}$$

• 小批量梯度下降：每次迭代使用一小部分数据来计算梯度，并更新参数

  • 减少了计算开销，比批量梯度下降更快，波动性比随机梯度下降小，因此更新更平稳，批量大小可调节

  • 仍具有一定随机性，可能导致收敛不稳定

    $$J(w,b)=\frac{\sum(\hat y_i-y_i)^2}{2n}\\w_{i}=w_{i-1}-\alpha\frac{\partial}{\partial w}J(w_{i-1},b_{i-1})\\b_{i}=b_{i-1}-\alpha\frac{\partial}{\partial b}J(w_{i-1},b_{i-1})\\w_0=w_{initial}\\b_0=b_{initial}$$

• 动量梯度下降 SGDM：在普通梯度下降的基础上引入动量的概念。动量会在每次更新时保留一部分上一次的更新方向，并在下次迭代中加以利用，从而加速收敛，尤其是在有很多局部最小值的非凸优化问题中。公式中 $\beta$ 为动量参数

  • 减少了梯度更新中的震荡，尤其是在凹凸形状的表面上；能加速梯度下降的收敛，特别是在长而平的曲面上

  • 需要调节额外的动量系数，并且对初始化较为敏感

    $$J(w,b)=\frac{\sum_{i=0}^n(\hat y_i-y_i)^2}{2n}\\p_{w,i}=\beta_wp_{w,i-1}+(1-\beta_w)\alpha\frac{\partial}{\partial w}J(w_{i-1},b_{i-1})\\w_{i}=w_{i-1}-p_{w,i}\\p_{b,i}=\beta_bp_{b,i-1}+(1-\beta_b)\alpha\frac{\partial}{\partial b}J(w_{i-1},b_{i-1})\\b_{i}=b_{i-1}-p_{b,i}\\w_0=w_{initial}\\b_0=b_{initial}$$

• 内斯特洛夫加速梯度 NAG：与上述的动量梯度下降法类似，但是它加入了前瞻性，也就是在计算当前的梯度时，会根据先前积累的动量向前迈一步，然后在那个未来的位置上计算梯度，然后利用这个前瞻的梯度来进行修正

  • 它通过提前修正，NAG 在接近最优点时不会像标准动量那样来回震荡，具有更稳定的收敛性

  • 在理论分析和许多实践中，NAG被证明具有比标准动量更优的收敛速率，尤其是在解决凸优化问题时

    $$J(w,b)=\frac{\sum_{i=0}^n(\hat y_i-y_i)^2}{2n}\\p_{w,i}=\beta_wp_{w,i-1}+(1-\beta_w)\alpha\frac{\partial}{\partial w}J(w_{i-1}-\beta_wp_{w,i},b_{i-1}-\beta_bp_{b,i})\\w_{i}=w_{i-1}-p_{w,i}\\p_{b,i}=\beta_bp_{b,i-1}+(1-\beta_b)\alpha\frac{\partial}{\partial b}J(w_{i-1}-\beta_wp_{w,i},b_{i-1}-\beta_bp_{b,i})\\b_{i}=b_{i-1}-p_{b,i}\\w_0=w_{initial}\\b_0=b_{initial}$$

• RMSProp：通过对过去的梯度平方进行指数加权平均，来动态调整学习率，使得参数更新更加平滑

  • 自适应学习率，有效应对学习率不适的问题，在非凸优化问题中表现优异，通常能够更快地收敛
  • 超参数 $\gamma$ 和 $\alpha$ 仍需要调节

  • 公式中 $\varepsilon$ 为一个小常数，防止除零错误，一般选择 $10^{-8}$

    $$p_{w,i} = \gamma_w p_{w,i-1} + (1 - \gamma_w)(\frac{\partial}{\partial w} J(w_i,b_i))^2\\w_{i+1} = w_i - \frac{\alpha}{\sqrt{p_{w,i}} + \varepsilon}\frac{\partial}{\partial w} J(w_i,b_i)\\p_{b,i} = \gamma_b p_{b,i-1} + (1 - \gamma_b)(\frac{\partial}{\partial b} J(w_i,b_i))^2\\b_{i+1} = b_i - \frac{\alpha}{\sqrt{p_{b,i}} + \varepsilon}\frac{\partial}{\partial b} J(w_i,b_i)$$

• Adam（Adaptive Moment Estimation）:结合了动量法和 RMSProp 的优点，既使用了梯度的一阶矩估计（动量），也使用了梯度的二阶矩估计（RMSProp 中的平方梯度）。通过对一阶和二阶矩进行修正，Adam 可以提供一个更平滑的更新过程

  • 具有自适应学习率，可以处理稀疏梯度，结合动量和 RMSProp 的优点，更新更加平滑和稳定，是目前深度学习中最常用的优化算法之一
  • 在某些情况下可能会产生较大的步长，导致模型的过拟合

  • 其中 $\beta_1$ 是控制一阶矩估计的指数衰减率（常用为 0.9）， $\beta_2$ 是控制二阶矩估计的指数衰减率（常用值为0.999）

    $$g_{w,i}=\frac{\partial}{\partial w} J(w_i,b_i)\\m_{w,i}=\beta_{w,1}m_{w,i-1}+(1-\beta_{w,1})g_{w,i}\\v_{w,i}=\beta_{w,2}v_{w,i-1}+(1-\beta_{w,2})g_{w,i}^2\\\hat{m}_{w,i}=\frac{m_{w,i}}{1-\beta_{w,1}^i}\\\hat{v}_{w,i}=\frac{v_{w,i}}{1-\beta_{w,2}^i}\\w_i=w_{i-1}-\alpha\frac{\hat{m}_{w,i}}{\sqrt{\hat{v}_{w,i}}+\varepsilon}$$

• Nadam：一种结合了 Nesterov 动量和 Adam 的优化算法。与 Adam 相比，Nadam 添加了 Nesterov 动量的修正，可以更好地处理稀疏梯度问题。在每次对梯度进行计算时，Nadam 算法会先获得一个参数临时更新量，对参数进行临时更新后计算获得临时梯度，利用临时梯度对一阶矩与二阶矩进行估计，并使用这些临时矩来计算参数的更新量

  • Nadam 算法通过结合 Nesterov 动量法，使得在更新参数时能够考虑前一步的速度，从而在某些情况下能够比 Adam 算法更快地收敛

  • 其中第二个值是修正之后的结果

    $$g_{w,i}=\frac{\partial}{\partial w} J(w_i,b_i)\\m_{w,i}=\beta_{w,1}m_{w,i-1}+(1-\beta_{w,1})g_{w,i}\\v_{w,i}=\beta_{w,2}v_{w,i-1}+(1-\beta_{w,2})g_{w,i}^2\\\hat{m}_{w,i}=\frac{m_{w,i}}{1-\beta_{w,1}^i}\\\hat{v}_{w,i}=\frac{v_{w,i}}{1-\beta_{w,2}^i}\\\bar{m}_{w,i}=\beta_{w,1}m_{w,i-1}+\frac{(1-\beta_{w,1})g_{w,i}}{1-\beta_{w,1}^i}\\w_i=w_{i-1}-\alpha\frac{\hat{m}_{w,i}}{\sqrt{\hat{v}_{w,i}}+\varepsilon}\\w_i=w_{i-1}-\alpha\frac{\bar{m}_{w,i}}{\sqrt{\hat{v}_{w,i}}+\varepsilon}$$

• Adadelta：一种自适应学习率算法，它通过动态调整每个参数的学习率来平衡学习速度和稳定性

  • Adadelta 可以自适应地调整每个参数的学习率，并且能够自动调整参数的动量，从而在收敛速度和精度方面表现出色
  • 通过自适应地调整学习率，Adadelta 算法通常能够加速模型的收敛过程

  • 其中 $\delta_p$ 表示参数更新量， $\delta$ 是累积更新量的指数加权平均（初始化为 0 或很小的值）， $\varepsilon$ 为一个小常数，通常选择 $10^{-8}$

    $$g_{w,i}=\frac{\partial}{\partial w} J(w_i,b_i)\\s_i=\rho s_{i-1}+(1-\rho)g_{w,i}^2\\\delta_p=-\frac{\sqrt{\delta_{i}+\varepsilon}}{\sqrt{s_{i}+\varepsilon}}g_{w,i}\\w_i=w_{i-1}+\delta_p\\\delta_i=\rho\delta_{i-1}+(1-\rho)\delta_p^2$$

典型类型

感知机网络

感知机网络是最简单的前馈神经网络，核心作用就是解决线性可分的二分类问题。感知机的本质就是单层的 FNN，仅包含输入层和输出层，无隐藏层

• 输入层由多个输入神经元组成，数量等于输入特征维度
• 输出层仅一个神经元，是感知机的核心计算单元，实现加权求和，后续连接一个激活函数

感知机网络的训练

感知机网络的训练核心是梯度下降法的简化版，通过误差修正更新权重和偏置，直到分类的误差收敛。

• 初始化权重和偏置项，一般权重初始化为一个小的随机数，偏置可以初始化为 0
• 通过前向传播计算预测结果 $\hat{y}$

• 权重更新，更新公式为

  $$w_i=w_i+\eta(y-\hat{y})x_i\\b_i=b_i+\eta(y-\hat{y})$$

• 之后重复迭代，直到满足需求

多层感知机 MLP

多层感知机是机器学习中一种基本且重要的神经网络模型，多层感知机由多个全连接层组成，即每一层的神经元与相邻层的所有神经元都相连。

多层感知机从输入层开始，经过隐藏层，最终到达输出层，每一层的神经元只接收来自前一层的输出作为输入，在每一个隐藏层之后都可以引入非线性激活函数，使得神经网络可以学习复杂的非线性

BP 网络

BP 神经网络的架构与上述的多层感知机一致，在更新和学习参数时，使用梯度下降法，并且利用反向传播的方法。通过前向传播计算损失，反向传播传递梯度，梯度下降更新参数，实现高效训练。

前向传播

数据从输入层开始，沿着设计好的神经网络，逐层计算直到在输出层得到一个预测的结果。这个过程是纯粹的计算过程，模型会利用它当前的参数，即权重和偏置，对输入的数据进行加工，最终输出一个结果。详细步骤如下：

• 将数据的样本送入网络的输入层
• 逐层计算：每一层都对上一层传输进来的数据进行处理
  • 线性变换：将上一层的输出与当前层的权重进行矩阵乘法并且加上偏置 $z=\vec{w}\vec{x}+b$
  • 激活函数：将线性变换的结果传入一个非线性的激活函数，得到当前层的最终输出 $a=f(z)$
  • 这个过程会一层接一层地进行下去，每一层的输出都将作为下一层地输入
• 最终输出：当所有数据流经过所有的隐藏层之后，最终到达输出层时，网络会生成一个最终的预测结果 $\hat{y}$

反向传播

反向传播的主要目的就是学习，是一个计算误差、计算梯度和更新参数的过程。

• 计算损失：首先是设计一个损失函数，损失函数就是定义的一个用于衡量模型预测结果好坏的标准，用于计算预测结果 $\hat{y}$ 和真实结果 $y$ 之间的差距
• 计算梯度：这是反向传播的关键一步，目标是更新网络中的每一个参数，让损失函数变得更小。利用微积分中链式法则，反向计算出损失函数对于网络中每一个参数的梯度，即 $\frac{\partial L}{\partial w}$ 和 $\frac{\partial L}{\partial b}$ 。
• 更新参数：有了每个参数的梯度，就可以利用优化器，来更新参数，更新的规则就是朝着损失下降最快的方向也就是梯度的反方向移动，移动的步长利用学习率 $\alpha$ 来控制，参数更新的规则为 $w=w-\alpha\frac{\partial L}{\partial w}$ 和 $b=b-\alpha\frac{\partial L}{\partial b}$

微积分的链式法则专门用于处理复合函数求导的问题。例如函数 $z=f(x,y),x=g(t),y=h(t)$

$$\frac{\partial z}{\partial t}=\frac{\partial z}{\partial x}\frac{\partial x}{\partial t}+\frac{\partial z}{\partial y}\frac{\partial y}{\partial t}$$

但是 BP 神经网络存在着梯度消失、过拟合、训练慢等问题

• 梯度消失
  • 可以选择其他的激活函数，例如使用 ReLU 代替 Sigmoid 或 Tanh
  • 使用 Adam 或 RMSprop 等自适应学习率优化器
• 过拟合
  • 加入 Dropout 层，训练时随机丢弃部分隐藏层神经元
  • 权重正则化，损失函数中加入正则化，限制权重大小
  • 监控验证集损失，及时停止，限制权重大小
• 训练效率低
  • 利用小批量梯度下降法
  • 训练后期降低学习率，避免权重震荡，促进收敛

RBF 网络

径向基（RBF）网络是一种以径向基函数为激活函数的神经网络，通过局部逼近的方式拟合非线性函数，与传统多层 FNN 的全局逼近不同。

RBF 函数

每个隐藏层的神经元对应着一个中心向量 $c_i$ ，维度与输入向量的维度一致，表示该神经元对输入空间的响应中心。而径向基函数的输出仅与输入向量 $x$ 和中心 $c$ 的欧式距离 $r=\Vert x-c\Vert$ 有关，是距离的一个单调函数

• 高斯 RBF 函数，其中 $\sigma^2$ 是方差

  $$f(r)=e^{-\frac{r^2}{2\sigma^2}}$$

• 反常 S 型函数

  $$f(r)=\frac{1}{1+e^{\frac{x^2}{\sigma^2}}}$$

• 多项式函数，其中 $d$ 是次数

  $$f(r)=(r+\sigma)^d$$

• 多重调和样条

  $$f(r)=\left\{\begin{aligned}&r^k&k=1,3,5,...\\&r^k\log(r)&k=2,4,6,...\end{aligned}\right.$$

• 薄板样条函数

  $$f(r)=r^2\log(r)$$

• 多二次函数

  $$f(r)=\sqrt{r^2+\sigma^2}$$

• 逆多二次函数

  $$f(r)=\frac{1}{\sqrt{r^2+\sigma^2}}$$

传统的 FNN 是全局逼近，任意一个输入的变化都会影响所有隐藏层的神经元的输出，而 RBF 网络是局部逼近的，只有输入靠近某个 RBF 神经元的中心时，该神经元才会产生显著的响应，其余神经元的输出接近 0

另外 RBF 的网络训练过程分为两步

• 学习隐藏层的中心 $c_i$ 和标准差 $\sigma_i$ ，标准差即宽度。常用的方法就是 K-Means 聚类，将聚类中心作为 RBF 的中心，宽度设置为聚类中心之间的平均距离
• 学习输出层的权重，由于输出层一般是线性的，所以可以通过最小二乘法直接求解，无需梯度下降迭代

深度神经网络 DNN

深度神经网络时多层前馈神经网络的延神，核心定义就是隐藏层数量至少为 2 的神经网络。它通过堆叠多层隐藏层，实现对数据的层次化特征提取，从而具备强大的复杂非线性拟合能力，也是深度学习的核心基础模型。深度神经网络通过多层的非线性变换，能从输入数据中自动学习并提取多层次和抽象的特征表示。

深度神经网络的训练与 BP 神经网络类似，都是使用前向传播+反向传播的方法来训练的，这里就不再赘述了，这些内容都算是比较简单的。

后记

FNN 是一种最基础的神经网络了吧，网络结构很简单。感知机模型只有输入输出层，而深度神经网络除此以外还有多个隐藏层，相应的，越复杂的网络结构对复杂信息的学习效果就越好，相应的训练的难度和参数数量也就越高。