循环神经网络

前言

循环神经网络 RNN 是一种对具有序列特性的数据非常有效，它能挖掘数据中的时序信息以及语义信息。它的核心特点就是网络中存在循环，可以使得信息可以从当前步骤传递到下一步骤，从而能够记住之前的信息。相当于是它是一个有记忆的网络，特别适合处理句子、时间序列等有前后依赖关系的数据。

传统的神经网络都有一个主要局限：假设输入是相互独立的，没有记忆功能，每次输入单独处理。循环神经网络中引入了上下文信息，作为当前时间步下网络的输出，传递给下一个时间步

模型识别评估方法

ACF 自相关函数

自相关指的是一个时间序列与其自身在不同时间点上的相似度，自相关系数范围为 $[-1,1]$

ACF 的作用：

• 周期性检测：通过观察 ACF 图中是否有显著的周期性波动，可以判断时间序列是否存在周期性
• 趋势分析：ACF 图可以帮助识别时间序列中的趋势，如果 ACF 随滞后增加而逐渐减小，说明序列存在趋势
• 随机性判断：如果 ACF 在所有滞后下都接近于 0，说明时间序列是随机的，可能不存在显著的自相关性

ACF 的自相关系数的计算公式如下

$$ACF(k)=\frac{\sum_{t=1}^{T-p}(x_t-\bar{x})(x_{t+p}-\bar{x})}{\sum_{t=1}^T(x_t-\bar{x})^2}$$

其中

• $x_t$ 是时间序列在 $t$ 时刻的值
• $\bar{x}$ 是时间序列的均值
• $p$ 是滞后阶数
• $T$ 是时间序列的长度

ACF 图是将不同滞后下的自相关系数绘制成图，其中 $x$ 轴表示滞后阶数， $y$ 轴表示对应的自相关系数。ACF 图在模型中主要用于确定自回归的阶数和移动平均阶数

在分析图时，会用到拖尾和截尾两个概念

• 拖尾是指序列以指数率单调递减或震荡衰减
• 截尾指序列从某个时点变得非常小

PACF 偏自相关函数

PACF 是偏自相关函数，偏自相关系数构成的序列。相较于 ACF 是衡量 $x_t$ 与 $x_{t-p}$ 之间的总相关性，PACF 是在移除了中间滞后项 $x_{t-1},\cdots,x_{t-p+1}$ 后 $x_t$ 与 $x_{t-p}$ 之间的直接相关性。

对于如下模型

$$x_t=\phi_0+\sum_{i=1}^p\phi_ix_{t-i}+\varepsilon_t$$

当求解 $x_t$ 与 $x_{t-p}$ 之间的直接关系，但是由于一般 $x_{t-1},\cdots,x_{t-p+1}$ 都是受到 $x_{t-p}$ 的影响的，所以在计算的时候需要排除掉这些其他的影响，下面是它的一些计算方法，这里不细说

• 最小二乘法
• 尤尔-沃克方程
• 伯格算法

AIC 赤池信息准则

AIC 信息准则是衡量统计模型拟合优良性的一种标准，它建立在熵的概念基础上，可以权衡所估计模型的复杂度和此模型拟合数据的优良性。

AIC 的标准公式如下

$$AIC=2k-2\ln(\hat{L})$$

其中

• $k$ 是模型中可自由估计的参数总数，而在 $AR(p)$ 中的参数数量为 $p+2$ 个
• $\hat{L}$ 是模型在给定数据之下的最大似然值，是模型对观测数据拟合优度的度量，它越大说明模型拟合得越好
• $\ln(\hat{L})$ 是最大似然值得自然对数

它的核心思想就是在模型拟合得优度和模型复杂度之间寻找平衡，上述的公式就分为两个部分

• $2k$ 即模型的参数数量，也就是模型的复杂度，它是模型复杂度的惩罚项，防止过拟合
• $-2\ln(\hat{L})$ 是衡量拟合优度，鼓励模型能更好的拟合数据

整体的逻辑就是，AIC 的值越小，整个模型的综合表现性能越好

BIC 贝叶斯信息准则

BIC 是统计学中用于模型选择的评价标准，与赤池信息准则同为模型选择的重要基准。

BIC 的标准公式如下

$$BIC=k\ln(n)-2\ln(\hat{L})$$

其中

• $k$ 是要估计的自由参数的数量
• $n$ 是用于拟合模型的有效样本观测数
• $\hat{L}$ 是模型的最大似然值

BIC 的结构与 AIC 相似，但是它们对模型复杂度的惩罚机制不同

• $k\ln(n)$ 即模型的参数数量，也就是模型的复杂度，它是模型复杂度的惩罚项，防止过拟合。另外当模型的样本量越多时，它对模型的惩罚力度就越强
• $-2\ln(\hat{L})$ 是衡量拟合优度，鼓励模型能更好的拟合数据

与 AIC 一样，BIC 的值越小，模型综合表现性能越好

DF 检验

全称是 Dickey-Fuller 检验，是一种基础的单位根检验方法，核心用法就是判断单变量时间序列是否平稳。它通过估计一个简单的自回归模型 $x_t=\rho x_{t-1}+\varepsilon_t$ 来检验滞后一阶的系数是否显著等于 1，检验模型有 3 种形式

• 无常数项和趋势项 $\Delta x_t=\lambda x_{t-1}+\varepsilon_t$
• 常数项 $\Delta x_t=\lambda x_{t-1}+\varepsilon_t+c$
• 有常数项和趋势项 $\Delta x_t=\lambda x_{t-1}+\varepsilon_t+\beta t+c$

检验假设

• 原假设 $H_0:\lambda=0$ ，则序列存在单位根，非平稳
• 备择假设 $H_1:\lambda<0$ ，则序列无单位根，平稳

ADF 检验

全称为 Augmented Dickey-Fuller 检验，由于上述的 DF 检验仅适用于 $AR(1)$ 序列，若序列是高阶自回归过程，那残差 $\varepsilon_t$ 可能会存在自相关性。导致 DF 检验结果失真。为了解决这种局限，衍生出 ADF 检验，在 DF 检验的回归方程的基础上加入了 $\Delta x_t$ 的滞后项，来消除残差的自相关性

与 DF 检验一致，ADF 检验根据序列的趋势特征分为三种模型形式，需通过时间序列可视化选择合适的形式，避免因模型选择错误导致检验偏差

• 无常数项和趋势项 $\Delta x_t=\lambda x_{t-1}+\sum_{i=1}^k\alpha_i\Delta x_{t-i}+\varepsilon_t$
• 常数项 $\Delta x_t=\lambda x_{t-1}+\sum_{i=1}^k\alpha_i\Delta x_{t-i}+\varepsilon_t+c$
• 有常数项和趋势项 $\Delta x_t=\lambda x_{t-1}+\sum_{i=1}^k\alpha_i\Delta x_{t-i}+\varepsilon_t+\beta t+c$

其中 $k$ 是滞后项，决定了残差自相关的消除效果，常用确定的方法如下

• 信息准则法：AIC、BIC 准则
• 逐步回归法：从较大的 $k$ 开始，逐步剔除不显著的滞后项

检验假设

• 原假设 $H_0:\lambda=0$ ，则序列存在单位根，非平稳
• 备择假设 $H_1:\lambda<0$ ，则序列无单位根，平稳

PP 检验

PP 检验全称为 Phillips-Perron 检验，是一种非参数化的单位根检验方法，核心用途是判断时间序列是否存在单位根，作为时间序列平稳性检验的重要手段。PP 检验的本质是改进后的 DF 检验，解决了 DF 检验无法处理残差自相关和异方差的问题，但是它的思路与 ADF 检验的思路不同

PP 检验不引入滞后项，直接对 DF 检验的统计量进行非参数修正，以此来同时处理残差的自相关性和异方差性，因此 PP 检验对残差存在异方差的时间序列的适应性更强

• 无常数项和趋势项 $\Delta x_t=\lambda x_{t-1}+\varepsilon_t$
• 常数项 $\Delta x_t=\lambda x_{t-1}+\varepsilon_t+c$
• 有常数项和趋势项 $\Delta x_t=\lambda x_{t-1}+\varepsilon_t+\beta t+c$

它的回归方程与 DF 检验的完全一致，而且它的检验假设也与 DF 的一致，但是她的判断规则有些改变，它的判断规则如下

1. 拟合对应的 DF 回归方程，计算未修正的 DF 统计量
2. 用核估计的方式修正 DF 统计量，得到 PP 统计量
3. 对比 PP 统计量与其临界值
   • 若 PP 统计量 $<$ 临界值：拒绝原假设，序列平稳
   • 若 PP 统计量 $\geq$ 临界值：接收原假设，序列非平稳

KPSS 检验

KPSS 检验的全称是 Kwiatkowski-Phillips-Schmidt-Shin 检验，是一种常用的单位根检验方法，核心特点与 ADF 和 PP 检验相反。

KPSS 将时间序列 $x_t$ 分解为确定性趋势项、随机游走项和平稳扰动项三个部分，分为两种模型形式

• 水平平稳 $x_t=\beta_0+r_t+e_t$
• 趋势平稳 $x_t=\beta_0+\beta_1t+r_t+e_t$

其中

• $\beta_0+\beta_1t$ 和 $\beta_0$ 为确定性趋势项
• $r_t=r_{t-1}+u_t$ 随机性游走项
• $e_t$ 平稳扰动项

检验假设

• 原假设 $H_0:Var(u_t)=0$ ，随机游走项不存在，序列平稳
• 备择假设 $H_0:Var(u_t)>0$ ，存在随机游走项，序列非平稳

简单来说，KPSS 检验是证明序列平稳，而 ADF/PP 检验是证明序列非平稳，两者结合使用可避免单一检验的误判

原始序列平稳性检验

在时间序列分析中，平稳性验证是建模前的核心步骤，非平稳序列会破坏时间序列模型的核心假设，导致伪回归和预测失效。

• 用非平稳序列构建回归模型时，即使两个序列没有实际关联，也可能得到显著的回归系数和高拟合优度，但是这种回归结果是虚假的
• 传统的时间序列建模要求序列平稳，非平稳序列的均值和方差随时间变化，会导致模型参数的估计值不具有一致性，无法反应序列的真实规律
• 非平稳序列的趋势或波动会随时间持续扩大，模型预测时会放大这种趋势偏差，用非平稳的经济增长序列预测未来值，会出现严重的高估或低估

平稳性分为严平稳（联合分布不随时间平移变化）和宽平稳（均值、方差恒定，自协方差仅与时间间隔有关），实际建模中主要验证宽平稳，常用方法如下

• 图形检验法
  • 时序图检验：绘制原始序列的折线图，观察均值和方差的变化。平稳序列中，折线图无明显上升或下降的趋势，波动范围稳定
  • 自相关函数 ACF 图检验：平稳序列的 ACF 值会快速衰减到置信区间内
• 统计检验法
  • DF 检验（Dickey-Fuller Test）
  • ADF 检验（Augmented Dickey-Fuller Test）：最常用的平稳性检验方法。
  • PP 检验（Phillips-Perron Test）
  • KPSS 检验（Kwiatkowski-Phillips-Schmidt-Shin Test）

当序列不平稳时，需要将非平稳序列平稳化处理，处理非平稳序列的核心思路是消除趋势性和季节性，常用方法如下

• 差分法：本质是计算序列相邻时刻的差值，消除线性趋势或随机游走趋势
  • 一阶差分：对于序列 $x_t$ 来说，一阶差分序列定义为 $\Delta x_t=x_t-x_{t-1}$
  • 高阶差分；若一阶差分后仍非平稳，可进行二阶差分 $\Delta^2x_t=\Delta x_t-\Delta x_{t-1}$ ，以此类推，直到序列平稳
  • 差分阶数不宜太高，否则会丢失序列的有效信息，通常 1-2 阶即可
• 季节性差分：适用于含周期性的非平稳序列
  • 对于存在季节性波动的序列，需要进行季节性差分 $\Delta_sx_t=x_t-x_{t-s}$ ，其中 $s$ 是季节周期长度
  • 如果同时存在趋势性和季节性，可先做季节性差分，再做普通差分
• 对数变换：适用于方差随时间扩大的序列
  • 对指数增长或方差递增的序列，先对序列取对数，可以压缩数据的波动幅值，使方差趋于稳定
  • 对数变换要求序列值均为正值，若存在 0 或负数，可先做平移处理
• 平滑法：适用于消除短期波动
  • 采用移动平均或指数平滑的方法，消除序列的随机波动，保留趋势项，再对趋势项进行差分处理
• 分解法：适用于趋势+季节+随机成分的序列
  • 将非平稳序列分解为趋势项、季节项和随机项三个部分，剔除趋势项和季节项之后，剩余的随机项通常是平稳的

传统时间序列模型

AR 自回归预测

自回归预测算法指的是利用预测目标的历史时间数列在不同时期取值之间存在的依存关系，建立起回归方程进行预测，即当前时刻的值是由过去若干时刻线性组合而成的。另外 AR 模型要求输入的时间序列必须是平稳的。整个工作流程如下

• 数据准备与理解：
  • 收集时间序列数据，确保数据是按时间排列的
  • 数据可视化：绘制时间序列图，检查数据的趋势性、季节性、异常值等
• 模型识别与模型阶数的确定
• 模型参数估计
• 模型检验：拟合模型之后检查是否充分合适
  • 残差分析：模型拟合的残差（实际值-预测值）应该类似于白噪声，可以利用绘制残差图、残差的 ACF 图、统计检验
  • 模型比较：尝试多个不同的阶数，利用信息准则来比较权衡阶数
  • 如果检验不通过，则需要重新调整阶数或者考虑复杂的模型
• 模型预测：模型通过检验之后，即可用于预测未来的值
  • 使用估计的参数和过去 $p$ 的实际值，带入模型公式进行递归计算
  • 除了给出点预测值，还应提供预测区间或置信区间，这给出了预测的不确定性范围
  • 对于多步预测，当需要预测的值超出已有的历史数据时，会用之前预测的值作为输入，进行递归预测。因此，预测步长越长，不确定性通常越大

AR 模型的公式定义如下，设时间序列为 $x_t$ ，而 $AR(p)$ 表示使用 $p$ 阶滞后项

$$x_t=\phi_0+\sum_{i=1}^p\phi_ix_{t-i}+\varepsilon_t$$

其中

• $p$ 是模型阶数，表示预测当前值需要用到的历史值得最大滞后阶数
• $c$ 是常数项
• $\phi_i$ 是自回归系数，表示过去各个时间点对当前值的影响程度
• $\varepsilon_t$ 是白噪声，并且 $\varepsilon_t\sim N(0,\sigma^2)$ ，代表模型无法使用历史数据解释的部分，通常假设其均值为 0，方差恒定，且各个时刻的误差相互独立

定阶数是 AR 模型中的关键步骤，定阶数的方法如下

• 自相关函数与偏自相关函数法，是最常用的定阶数的方法
  • ACF 自相关函数：衡量 $x_t$ 与 $x_{t-p}$ 之间的总相关性，包含了通过中间变量的间接影响
  • PACF 偏自相关函数：衡量在排除中间滞后项影响后的 $x_t$ 与 $x_{t-p}$ 之间的直接相关性，即在控制了中间变量之后 $x_{t-p}$ 对 $x_t$ 的额外影响
• 信息准则法：通过量化模型拟合优度与复杂度，选择最优阶数。遍历可能的取值，计算对应的 AIC 或 BIC 的值，最小值对应的阶数就是最优阶数
  • 赤池信息准则 $AIC=2k-2\ln(L)$ ，其中 $L$ 为似然函数值，参数总数为 $k=p+2$
  • 贝叶斯信息准则 $BIC=p\ln(n)-2\ln(L)$ ，其中 $n$ 为样本量

AR 模型必须满足平稳性条件才有良好的统计性质，它的特征方程如下

$$1-\sum_{i=1}^p\phi_iz^i=0$$

而 AR 模型的平衡条件就是特征方程的所有根的模大于 1。模型参数的常用估计方法

• 最小二乘法：通过最小二乘法通过最小化误差项的平方和来估计参数
  • 构建目标函数 $S(\phi)=\sum_{t=p+1}^T(X_t-c-\sum_{i=1}^p\phi_iX_{t-i})^2$
  • 对目标函数求偏导，并令其等于 0，求解方程组得到参数估计值
• 极大似然估计法：通过极大似然估计函数来估计参数
  • 似然函数 $L(\phi,c,\sigma^2)=\prod_{t=p+1}^T\frac{1}{\sqrt{2\pi\sigma^2}}exp(-\frac{(X_t-c-\sum_{i=1}^p\phi_iX_{t-i})^2}{2\sigma^2})$
  • 最大化对数似然函数得到估计值

VAR 向量自回归模型

VAR 模型是一种用于分析多变量时间序列关系的计量经济模型，核心特点是所有变量均被视作内生变量，每个变量的当前值由自身及其其他所有变量的历史滞后值共同解释，模型记作 $VAR(p)$ ，其中 $p$ 表示滞后阶数

假设存在 $k$ 个平稳的时间序列变量 $x_{1t},x_{2t},\cdots,x_{kt}$ ，将其组成 $k\times1$ 的向量

$$X_t=\begin{bmatrix}x_{1t}\\x_{2t}\\\cdots\\x_{kt}\end{bmatrix}$$

则 $VAR(p)$ 的完整公式如下

$$X_t=\phi_0+\sum_{i=1}^p\phi_iY_{t-i}+\varepsilon_t$$

其中

• $\phi_0$ 是 $k\times1$ 的常数向量
• $\varepsilon_t$ 是 $k\times1$ 的随机扰动向量

MA 移动平均模型

移动平均模型是传统时间序列分析中最基础的模型之一，核心聚焦于误差项的累积影响，与自回归模型的历史数据依赖形成互补。MA 模型假设：时间序列的当前值由当前的随机误差和过去 $q$ 个时刻的随机误差线性组合而成的，而非直接依赖历史观测值，适合平稳且误差项存在自相关的时间序列

对于平稳时间序列， $q$ 阶移动平均模型记作 $MA(q)$ ，数学表达式为

$$x_t=\theta_0+\sum_{i=1}^p\theta_i\varepsilon_{t-i}+\varepsilon_t$$

其中

• $\theta_0$ 为常数项，也就是序列的均值水平
• $\varepsilon_t$ 是在 t 时刻的白噪声，并且 $\varepsilon_t\sim N(0,\sigma^2)$ ，并且在不同时刻的 $\varepsilon$ 相互独立
• $\theta_i$ 是移动平均系数，是模型的待估计参数
• $q$ 是模型的阶数

模型的阶数 $q$ 的确定是构建 MA 模型的关键步骤，它的核心方法如下。

• 绘制 ACF 图，观察自相关系数的衰减规律，如果 ACF 图在滞后 $q$ 阶滞后突然截尾，即自相关系数趋近于 0，且落在置信区间内，则判定模型阶数为 $q$
• 利用信息准则：可结合信息准则遍历不同的 $q$ 值，选择最优阶数
  • AIC 信息准则
  • BIC 信息准则

在选定 $q$ 后，拟合 $MA(q)$ 模型，检验残差是否为白噪声（即残差的 ACF 无显著自相关）。若残差不是白噪声，说明 $q$ 选择不合理，需调整阶数。

MA 模型的核心特点如下

• 关注误差的滞后影响，本质是对预测误差的平滑，即过去某一时刻的随机的误差不会仅影响当期，还会持续影响后续 $q$ 个时刻的序列值
• 有限记忆性：模型的记忆长度为 $q$ ，当滞后阶数超过 $q$ 时，过去的误差项不再对当前值产生影响，而 AR 模型理论上是由无限记忆的
• 可逆性：当 MA 模型的特征方程的所有根的绝对值都大于 1 时，MA 模型可以转化为无穷阶的 AR 模型，同时确保参数估计的唯一性

MA 模型的特征方程为

$$1+\sum_i^p\theta_iz^i=0$$

但是 MA 模型仅能捕捉误差项的线性依赖，无法处理非线性关系，要求序列必须平稳，非平稳的序列需要先做差分处理。另外就是高阶的 MA 模型，参数估计的计算量会显著增加

ARMA 自回归移动平均模型

ARMA 时自回归滑动平均模型，是研究时间序列的重要方法，由 AR 自回归模型和 MA 移动平均模型为基础混合而成。它的核心就是同时捕捉时间序列的历史观测值依赖和历史误差项依赖，仅适用于平稳的时间序列

对于平稳的时间序列 $x_t$ ， $ARMA(p,q)$ 就是 $p$ 阶自回归 + $q$ 阶移动平均的模型，公式如下

$$x_t=c+\varepsilon_t+\sum_{i=1}^p\phi_ix_{t-i}+\sum_{i=1}^q\theta_i\varepsilon_{t-i}$$

其中

• $x_t$ 是时间序列在 $t$ 时刻的观测值
• $c$ 是模型的常数项，代表序列的均值水平
• $p$ 是自回归部分的阶数
• $\phi_i$ 是自回归系数，表示过去各个时间点对当前值的影响程度
• $q$ 是移动平均部分的阶数
• $\theta_i$ 是移动平均系数，是模型的待估计参数
• $\varepsilon$ 是 $t$ 时刻的白噪声，满足 $\varepsilon\sim N(0,\sigma^2)$

$ARMA(p,q)$ 的自相关函数和偏自相关函数均出现拖尾特性

• AR 模型：PACF 截尾，ACF 拖尾
• MA 模型：ACF 截尾，PACF 拖尾
• ARMA 模型：ACF 和 PACF 均拖尾

因此在确定 ARMA 模型的阶数时，无法仅通过 ACF 或 PACF 图来精确判断，通常需要结合 AIC 或 BIC 信息准则遍历参数组合。另外与 MA 模型类似， ARMA 模型也需要满足可逆性，即保证模型参数的唯一性，避免同一组观测数据对应多组参数接，可逆性的核心是 MA 部分的特征方程根的绝对值大于 1

ARIMA 自回归积分移动平均模型

ARIMA 模型时时间序列预测领域的经典模型，核心结构由自回归、差分、移动平均三个部分组成，模型记作 $ARIMA(p,d,q)$ 。ARIMA 的完整模型公式如下

$$\Delta^dx_t=c+\varepsilon_t+\sum_{i=1}^p\phi_i\Delta^dx_{t-i}-\sum_{i=1}^q\theta_i\varepsilon_{t-i}$$

其中的三个部分如下

• 自回归部分：当前时刻的序列值与前 $p$ 个时刻的序列值线性相关
• 差分部分：差分的作用是消除时间序列的趋势性和季节性，使其转化为平稳序列，其中 $d$ 表示对原始序列的差分次数
  • 一阶差分 $\Delta x_t=x_t-x_{t-1}$ ，消除线性趋势
  • 二阶差分 $\Delta^2x_t=\Delta x_t-\Delta x_{t-1}$ 用于消除二次趋势
  • 如果原始序列本身是平稳的，则设置 $d=0$
• 移动平均部分：当前时刻的序列值与前 $q$ 个时刻的白噪声扰动线性相关

SARIMA 季节性自回归积分移动平均模型

SARIMA 是 ARIMA 模型的扩展，专门用于处理同时包含趋势性和季节性的非平稳时间序列，模型记作 $SARIMA(p,d,q)(P,D,Q)_s$ ，其中包含非季节性参数和季节性参数两组核心参数。它的核心思想就是对时间序列同时进行非季节性差分和季节性差分，再结合非季节性、季节性的自回归和移动平均项建模。完整的计算公式如下

$$\phi_p(B)\Phi_P(B^s)\Delta^d\Delta^D_sx_t=c+\theta_q(B)\Theta_Q(B^s)\varepsilon_t$$

其中

• $B$ 是滞后算子，如 $B^kx_t=x_{t-k}$
• $\phi_p(B)=1-\sum_{i=1}^p\phi_iB^i$ 是非季节性 AR 算子
• $\Phi_P(B^s)=1-\sum_{i=1}^P\Phi_iB^{is}$ 是季节性 AR 算子
• $\theta_q(B)=1-\sum_{i=1}^q\theta_iB^i$ 是非季节性 MA 算子
• $\Theta_Q(B^s)=1-\sum_{i=1}^Q\Theta_iB^{is}$ 是季节性 MA 算子

ARIMAX 带有外部变量的自回归积分移动平均模型

ARIMAX 是 ARIMA 模型的扩展，核心是在原有结构中引入了外部解释变量，用于受理外部因素影响的时间序列预测问题，模型记作 $ARIMAX(p,d,q)$ 。ARIMAX 是在 ARIMA 模型的基础上加上外部变量项，核心思想就是，时间序列的当前值不仅与自身历史值和历史扰动项相关，还与一个或多个外部变量的当前值或历史值相关

$$\Delta^dx_t=c+\varepsilon_t+\sum_{i=1}^p\phi_i\Delta^dx_{t-i}-\sum_{i=1}^q\theta_i\varepsilon_{t-i}+\sum_{i=1}^k\beta_kx_{t,k}$$

它的核心参数数量与 ARIMA 完全一致，设外部变量为 $x_{t,k}$ ，其中 $t$ 为时间戳， $k$ 是外部变量的个数。外部变量需要满足与时间序列相关，但不受时间序列影响的条件。上述的公式中包含 4 个部分

• 自回归部分：当前时刻的序列值与前 $p$ 个时刻的序列值线性相关
• 差分部分：差分的作用是消除时间序列的趋势性和季节性，使其转化为平稳序列，其中 $d$ 表示对原始序列的差分次数
  • 一阶差分 $\Delta x_t=x_t-x_{t-1}$ ，消除线性趋势
  • 二阶差分 $\Delta^2x_t=\Delta x_t-\Delta x_{t-1}$ 用于消除二次趋势
  • 如果原始序列本身是平稳的，则设置 $d=0$
• 移动平均部分：当前时刻的序列值与前 $q$ 个时刻的白噪声扰动线性相关
• 外部变量项：外部引入的变量 $x_{t,k}$ 需要是平稳序列，如果不平稳需要先进行差分处理

引入外部的变量项在实际使用中，外部变量的影响可能存在滞后，此时可以引入外部变量的滞后项来缓解，将公式扩展为

$$\Delta^dx_t=c+\varepsilon_t+\sum_{i=1}^p\phi_i\Delta^dx_{t-i}-\sum_{i=1}^q\theta_i\varepsilon_{t-i}+\sum_{i=1}^k\sum_{j=0}^l\beta_{k,j}x_{t-l,k}$$

其中的 $l$ 为外部变量的最大滞后阶数。

另外如果同时引入季节性因素和外部变量的话，则可扩展为 SARIMAX 模型 $SARIMAX(p,d,q)(P,D,Q)_s$

一些经典的 RNN

Elman RNN

Elman RNN 是最早的 RNN 架构之一，目的就是为了处理时间序列数据并且学习其中的时间依赖模式。最核心的创新就是引入了上下文单元，也就隐藏状态，这个状态会在时间步之间循环传递，作为网络的记忆。

RNN 的核心是循环单元，单步循环单元的输入输出关系如下

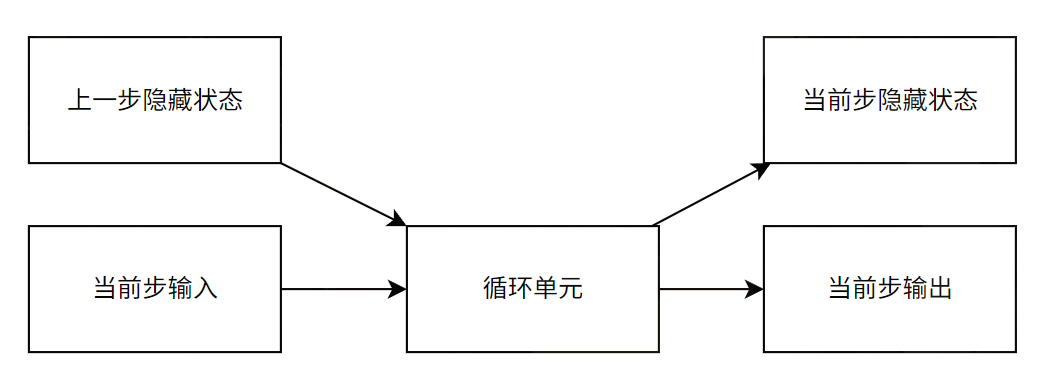
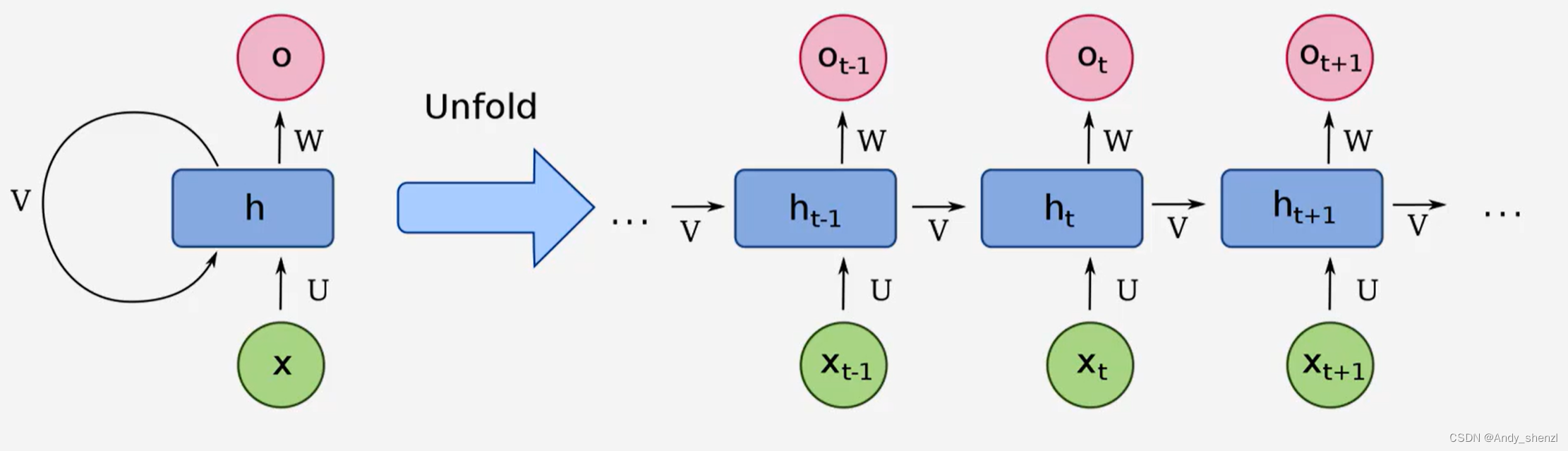
将循环神经网络的隐藏层展开，展开的示意图如下所示

如图中所示，其中 $x(t)$ 是 t 时刻的输入向量， $h(t)$ 是 t 时刻的隐藏状态， $y(t)$ 是 t 时刻的输出，每个时刻都是共享同一组参数。对于单个时间步 $t$ 来说，在 $t$ 时刻中

$$h(t)=\tanh(Wh(t-1)+Ux(t)+b_h)\\y(t)=Vh(t)+b_y$$

其中 $W$ 是隐藏状态到隐藏状态的权重矩阵， $U$ 是输入到隐藏状态的权重矩阵， $V$ 是隐藏状态到输出的权重矩阵， $b_y,b_h$ 是偏置项，在 RNN 中的激活函数通常采用 $\tanh$ 函数或者 $ReLU$ 函数。

Elman RNN 使用 BPTT 算法进行训练，网络的先过程如下

• 前向传播整个序列，计算每个时间步的损失
• 从最后一个时间步开始，反向计算损失对每个参数在每个时间步的梯度，由于参数在所有时间步共享，所以梯度会沿着时间轴一直向后传播
• 将所有时间步的梯度累加，然后更新参数

Elman RNN 的结构比较简单，清晰的展示了循环神经网络的核心思想，就是利用循环连接维护网络状态。而且 RNN 的模型参数很少，使其能泛化到不同步长的序列。

但是 Elman RNN 最大的缺陷就是梯度消失或梯度爆炸的问题，在 BPTT 过程中，梯度需要沿着时间步连续相乘，对于长序列，梯度会发生梯度消失或梯度爆炸，导致网络无法学习到长距离的依赖关系。而且由于更新机制比较简单，隐藏状态在每次更新的时候都会被重写，难以长期保存精确信息。

Jordan RNN

Jordan RNN 网络是最早，最简单的循环神经网络之一，它为解决序列处理问题提供了一种基础的反馈机制。它的核心思想就是将网络的输出在下一个时间步反馈到输入层，这使得网络能够记住自己之前的决策，从而处理与时间相关的模式。

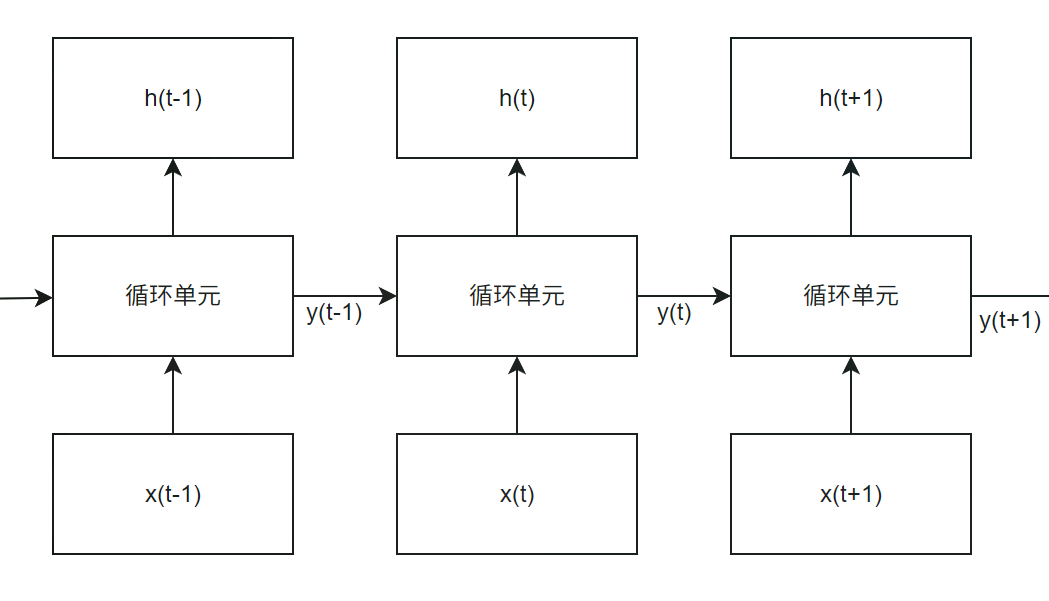
在每一步运行时，除了接收外部输入以外，还会接收来自网络的上一时间步的输出作为额外的输入。将当前外部输入和上一时间步的输出连接起来，形成扩展的输入向量，计算隐藏状态时，通常将反馈的输出直接作为额外的输入接入隐藏层的。

$$h(t)=\tanh(W_{xh}x(t)+W_{ch}y(t-1)+b_h)\\y(t)=W_{hy}h(t)+b_y$$

Jordan RNN 的反馈的信息是输出层的信息，记忆的并非是隐藏状态，而是之前的决策。由于它反馈的只是当前时间步下的最终输出，而不是更丰富的隐藏状态，这就限制了 RNN 的记忆的能力。

RNN Encoder-Decoder

RNN Encoder-Decoder 的核心思想就是将输入序列编码成一个固定维度的上下文向量，然后再用这个向量解码成目标序列，它完美的解决了从序列到序列之间的映射问题。整体结构如下

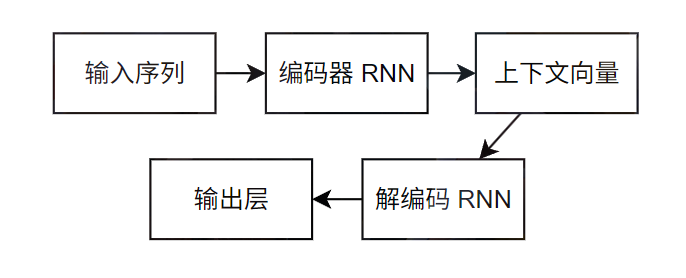
• 编码器 RNN：通常是一个循环神经网络
  • 输入一个可变长度的原始序列，编码器按顺序逐个读取原序列的每个元素，在每一步都更新其隐藏状态，这个隐藏状态包含了到目前为止的所读序列的信息。
  • 读完最后一个输入之后，编码器的最终隐藏状态就作为整个输入序列的上下文向量输出。如果中间的编码器是双向的 RNN，那通常就是两个 RNN 的拼接。
• 上下文向量：是整个模型的关键，是一个固定大小的向量，所有输入序列的信息，无论多长都需要流经这个固定的维度的向量
• 解码器 RNN：另一个独立的循环神经网络，将上下文向量按顺序输入到 RNN 中。基于上一步的隐藏状态和输出，计算出新的隐藏状态，并且预测当前步的输出作为下一步的输入。当前步的输出就是当前预测的概率最大的结果。

RNN Encoder-Decoder 将所有的输入信息都压缩进一个固定长度的上下文向量中，可以处理输入和输出长度不同的任务，但是当序列过长就导致难以保留全部细节信息，导致性能下降。

长短期记忆神经网络 LSTM

长短期记忆神经网络，是一种特殊的循环神经网络，是循环神经网络的重要突破。传统简单的 RNN，只能处理较接近的上下文情况，能获取的上下文的信息很短，有些时候需要非常远的上下文信息，但是 RNN 导致长时间前的有用的信息被忽略掉了。LSTM 的设计就是为了解决这个问题的，同时 LSTM 也能解决 RNN 中的梯度消失或者梯度爆炸的问题。

LSTM 的核心创新就是引入了门控单元，能够有选择地保留、遗忘和更新信息，通过设计流程来传递长期信息，避免了梯度消失的问题。另外 LSTM 有两个状态变量，单元状态 $C_t$ 和隐藏状态 $h_t$

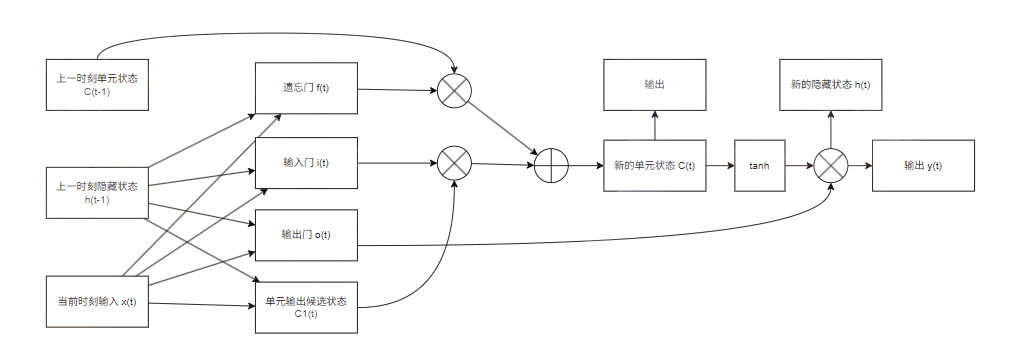
每个单元的结构

• 核心记忆单元：单元状态，用 $C_t$ 表示，在时间步之间流动，只受到少量线性操作的影响，使得梯度能稳定传播

• 候选值：接收上一层的输出值，生成可能加入单元状态的新信息

  $$\tilde{C}_t=\tanh(W_C[h_{t-1},x_t]+b_C)$$

• 三个门控结构：三个门结构每一个都是 Sigmoid 神经网络层，输出值为 0 到 1 之间，决定信息通过的量

  • 遗忘门：决定丢弃什么信息，输出 0 时完全遗忘，输出 1 时完全保留

    $$f_t=\sigma(W_f[h_{t-1},x_t]+b_f)$$

  • 输入门：决定哪些信息存入单元状态

    $$i_t=\sigma(W_i[h_{t-1},x_t]+b_i)$$

  • 输出门：决定输出的信息，其中 $h_t$ 就是新的隐藏状态，也是当前时间步的输出，其中 $\odot$ 是逐元素相乘

    $$o_t=\sigma(W_o[h_{t-1},x_t]+b_o)\\h_t=o_t\odot \tanh(C_t)$$

• 更新单元状态：基于遗忘门和输入门的决定，更新单元状态

  $$C_t=f_t\odot C_{t-1}+i_t\odot \tilde{C}_{t}$$

• 最终输出：一般是直接输出 $h_t$ ，但是在构建一个完整的、用于解决实际任务的神经网络时， $h_t$ 通常不是最终的答案，此时在后续可以连接一个输出层。例如对于多分类任务，输出为 $y_t=softmax(W_yh_t+b_y)$

LSTM 模拟了人类的记忆的过程，选择遗忘不重要的过去，专注于当前重要的信息，并且有控制地输出。

Peephole 连接

Peephole 连接是 lSTM 的一种变体结构，在传统的 LSTM 门控单元中，额外增加了从单元状态到各个门的加权连接。在标准的 LSTM 中，通过三个门来控制信息流，这三个门的计算只依赖于 $h_{t-1}$ 和 $x_t$ ，所以门在决定开关时，并没有直接看到单元状态本身的值 $C_{t-1}$ 。Peephole LSTM 中提出让门控单元窥探单元状态的内容，可能有助于做出更精确的决策。将三个门的方程设计为如下的形式

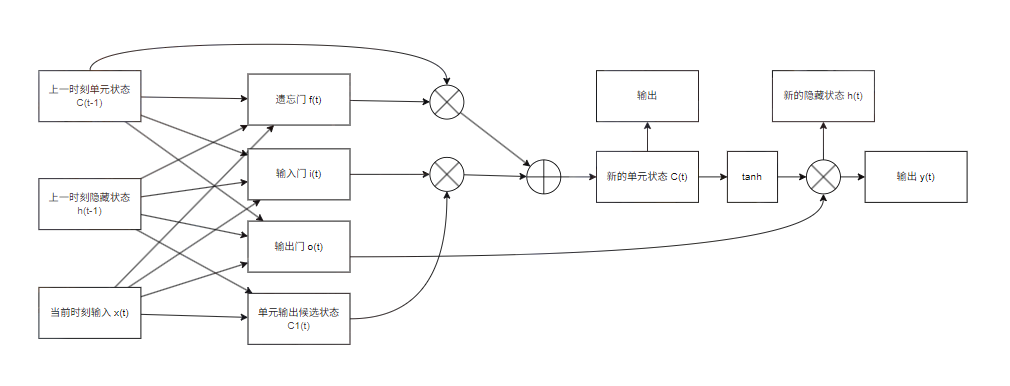
• 遗忘门：窥探上一时刻的单元状态 $C_{t-1}$

  $$f_t=\sigma(W_f[C_{t-1},h_{t-1},x_t]+b_f)$$

• 输入门：窥探上一时刻的单元状态 $C_{t-1}$

  $$i_t=\sigma(W_i[C_{t-1},h_{t-1},x_t]+b_i)$$

• 输出门：窥探当前时刻更新之后的单元状态 $C_t$

  $$o_t=\sigma(W_o[C_t,h_{t-1},x_t]+b_o)$$

Peephole 为模型提供了更精细的控制能力，能在某些任务上提高性能，但是它为每个门都增加了相关的权重，这提高了模型的复杂度。由于输出门依赖于当前步计算出的 $C_t$ ，它引入了额外的计算依赖，使得并行化计算变得更加复杂。

双向 LSTM

双向长短期记忆网络是一种经典的序列建模神经网络结构，在标准的 LSTM 的基础上增加了逆向时间序列的信息传递，从而能够同时利用过去和未来的上下文信息。通过增加一个从后向前处理的 LSTM 层，使当前时刻的输出能同时依赖于过去和未来的上下文信息。

• 前向的 LSTM：按照时间顺序从前向后处理序列
• 反向的 LSTM：按照时间顺序从后向前处理序列

它的参数数量是单向 LSTM 的两倍，训练时两个方向同时进行反向传播

TCN-LSTM

TCN-LSTM 是一种结合了卷积神经网络时序建模能力和循环神经网络长距离依赖捕捉能力的混合神经网络结构，旨在克服各自模型的局限性，提供更强大的时间序列建模能力。

• TCN 的优点：并行计算、感受野可控、梯度稳定等
• LSTM 的优点：长距离依赖、顺序建模、状态记忆等
• 结合之后，利用 TCN 提取局部特征，再利用 LSTM 建模长期依赖关系

TCN 和 LSTM 的连接结构如下

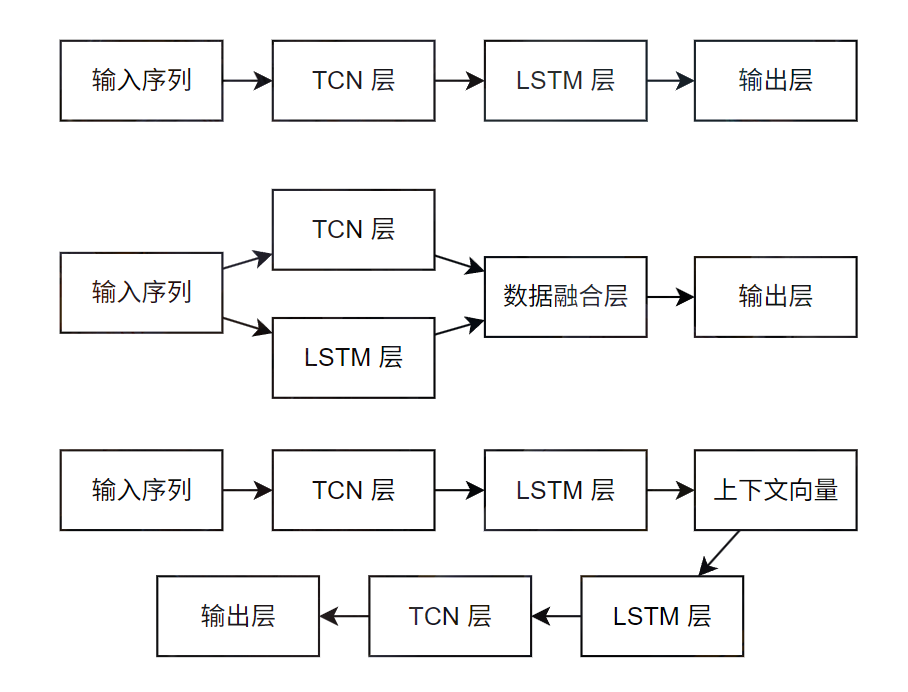
• 串联结构
  • TCN 作为特征提取器：提取时间序列的局部模式和层次特征
  • LSTM 作为时序建模其：对 TCN 提取的特征序列建模
• 并联结构
• 编码器-解码器结构

TCN 层是专门为时序数据设计的卷积神经网络，主要作用就是局部特征提取与并行计算，中是由多个残差块堆叠而成的，每个残差块中包含的特性如下

• 因果卷积：卷积核仅作用于当前时刻以及历史时刻的数据，避免未来信息泄露
• 空洞卷积：通过再卷积核中引入空洞，在不增加参数的前提下扩大感受野
• 残差连接：缓解深层网络梯度消失问题，确保特征在传递过程中不丢失

门控循环单元 GRU

GRU 是 LSTM 的一种简化的变体，旨在保持 LSTM 性能的同时减少参数和计算复杂度。将 LSTM 的三个门简化为了两个门，两个 Sigmoid 神经网络层

每个单元的结构

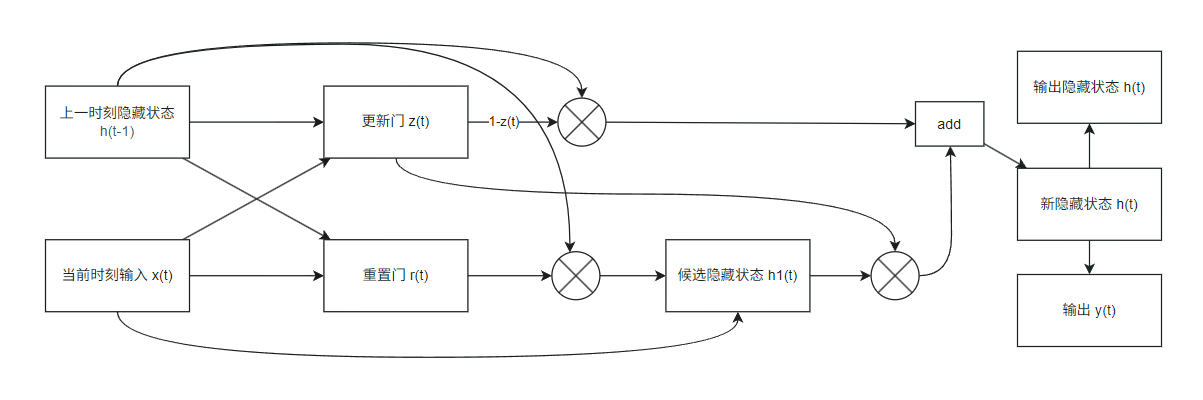
• 更新门：同时控制遗忘和记忆的程度，决定新旧信息的融合比例，用于计算候选隐藏状态

  $$z_t=\sigma(W_z[h_{t-1},x_t]+b_z)$$

• 重置门：控制对过去信息的忽略程度，决定有多少信息需要被忘记或重置

  $$r_t=\sigma(W_r[h_{t-1},x_t]+b_r)$$

• 候选的隐藏状态：生成可能加入隐藏状态的新信息

  $$\tilde{h}_t=\tanh(W[r_t\odot h_{t-1},x_t]+b)$$

• 最终隐藏状态更新，新旧信息加权组合

  $$h_t=(1-z_t)\odot h_{t-1}+z_t\odot \tilde{h}_t$$

GRU 在保持 LSTM 的核心能力的同时，也提供了更高的计算效率，更简洁的框架，在实际使用中，它们两个的性能差异很小。

双向 GRU

双向 GRU 是 GRU 的一个扩展，旨在利用过去和未来的上下文信息，来增强序列数据的处理能力。对于单向的 GRU 在编码一个序列时，每个时间步的隐藏状态只依赖于当前时刻以及之前的输入，而双向的 GRU 通过结合两个独立的 GRU 层来克服这个限制。双层的 GRU 结构由两个独立的 GRU 组成

• 前向的 GRU：按时间顺序处理输入序列
• 反向的 GRU：按时间逆序处理输入序列

之后将两个方向在每个时间步产生的隐藏状态进行组合，形成最终的输出

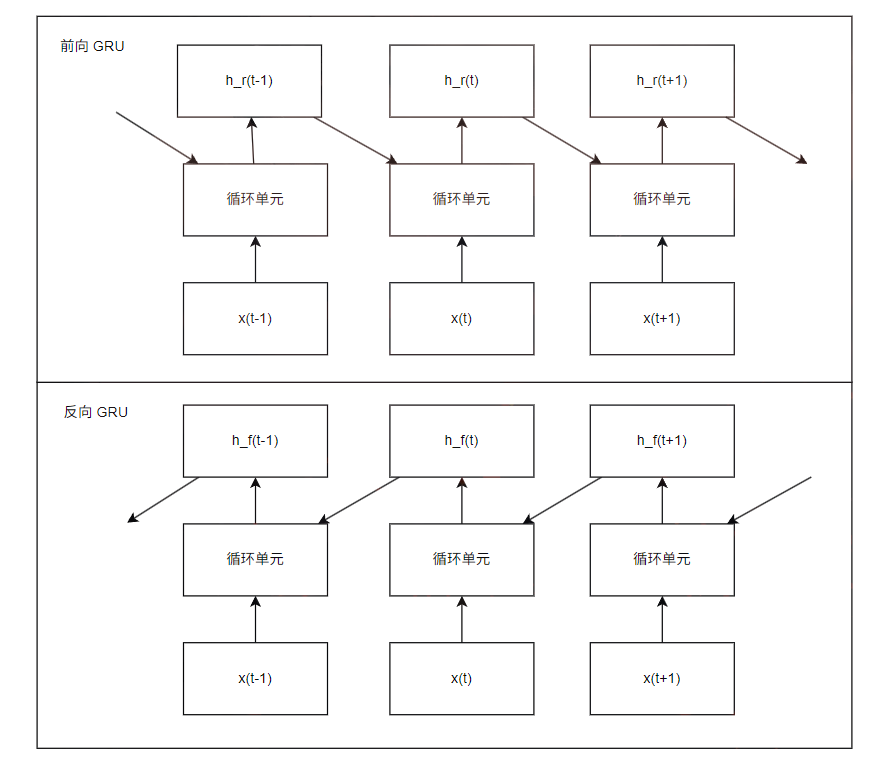
在每个时间步中，双向 GRU 会结合两个独立的 GRU 生成一个最终的输出向量 $h(t)$ ，比较常用的组合有三种

• 拼接：将两个方向的隐藏状态在特征维度上拼接起来 $h(t)=[h_f(t),h_r(t)]$ ，保留了前后向 GRU 的全部信息
• 求和：将两个方向的隐藏状态逐个元素相加 $h(t)=h_f(t)+h_r(f)$ ，减少了参数和计算量，属于是一种参数融合
• 平均：将两个方向的隐藏状态取均值 $h_t=\frac{h_f(t)+h_r(t)}{2}$ ，对两个方向上的信息进行平滑操作

双向 GRU 在最终的处理中，有着相较于 GRU 更多的上下文信息，最终输出的组合方式可以根据任务需求选择。但是参数和计算量是单向 GRU 的两倍，而且必须要等待完整的输入序列才能开始反向处理。

深度 GRU

深度 GRU 通过堆叠多个 GRU 层来构建更深的网络，以学习更抽象更复杂的序列特征。深层 GRU 的核心就是多个 GRU 层的堆叠，前一层的输出序列作为后一层的输入序列，深度 GRU 可以捕捉更复杂的时序依赖关系和模式。

• 底层：学习局部低级的时序模式
• 中层：学习中等范围的模式
• 高层：学习全局的高级的语义

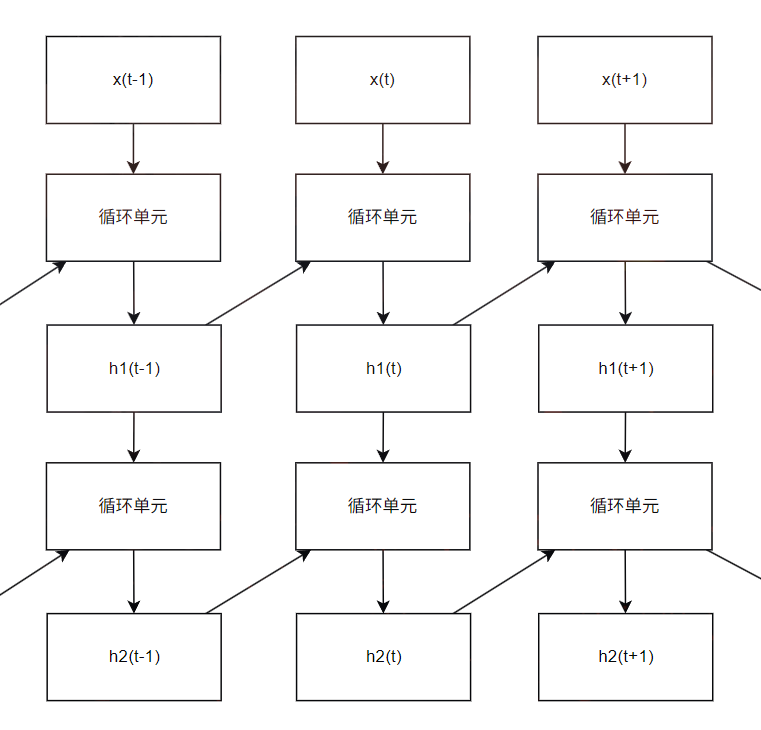
在时间步 $t$ 时，每一层的输入输出状态如下

• 第一层 $h_t^1=GRU^1(x_t,h_{t-1}^1)$
• 第 $l$ 层 $h_t^l=GRU^l(h_{t}^{l-1},h_{t-1}^l)$
• 最终输出 $output=h_t^L$

在深度 GRU 中，每一层之间的连接方式有多种

• 标准堆叠：第 $l$ 层的输入就是第 $l-1$ 层的输出
• 残差连接：
• 密集连接：第 $l$ 层的输入为当前前面所有层输出的拼接

TCN-GRU

与上述的 TCN-LSTM 一样，只是 TCN 与 GRU 的组合，这里就不再赘述了

回声状态网络 ESN

Echo State Network 回声状态网络，是一种特殊的递归神经网络，核心特点就是通过稀疏随机连接的动态储备池替代传统的 RNN 隐藏层，无需训练隐藏层的权重，仅优化输出层连接权重，大幅度降低了训练的复杂度。它的结构可以分为三个部分：输入层、储备池、输出层

• 输入层：接收外部时序数据，将其映射到储备池的输入空间

• 储备池：核心的动态层，通过稀疏随机连接产生复杂的非线性响应，记忆输入序列的历史信息。

  • 储备池有两个权重矩阵，输入权重 $W_i$ 和循环权重 $W_h$ ，还可以选择使用储备池偏置项 $b$
  • 输入权重随机采样自 $[-a, a]$ ，通常 $a\in[0.5,1.0]$ ，确保输入信号能有效驱动储备池
  • 循环权重随机采样自 $[-1,1]$ ，再通过稀疏化和谱半径调整，满足回声状态条件，即保证储备池状态不会随时间发散，且能对输入序列产生持续的影响
  • 储备池能记住输入序列的历史信息，记忆的长度与节点数、稀疏度和谱半径相关

  • 在储备池中通过稀疏循环连接和激活函数，将线性输入转化为高维的非线性特性空间，如下的 $f()$ 就是激活函数

    $$h(t)=f(W_ix(t)+W_hh(t-1)+b)$$

• 输出层：线性组合储备池状态与输入信号，输出最终结果

  • ESN 的训练过程比传统的 RNN 简单很多，核心就是求解输出层的权重
  • 将整个训练时序数据输入到 ESN 中之后，记录每个时刻的输入 $x_t$ 和储备池的状态 $h_t$ ，构建矩阵 $X=[x_1,h_1,…x_n,h_n]$ ，网络最终的输出为 $Y=W_oX$ ，而与输入信息对应的目标矩阵为 $Y=[y_1,…y_n]$ ，其中的 $W_o$ 是唯一需要训练的参数
  • 最后通过最小二乘法最小化损失函数 $Loss=\Vert Y-W_oX\Vert_2^2$ ，可以加入正则化避免过拟合，最终的解为 $W_o=YX^T(XX^T\lambda I)^{-1}$
• 回声状态条件：ESN 的储备池必须满足回声条件才能保证模型稳定且具有记忆能力
  • 定义：对于任意有界的序列输入，储备池的状态最终会收敛到有界的区域，且不同的初始状态的影响会逐渐消失
  • 判断条件：循环权重的谱半径小于 1
  • 实现方式：对随机生成的权重，先计算其谱半径，之后再将其缩放到 0.8~0.95 之间

ESN 的结构设计需要在以下的几个参数上进行权衡，以适配具体的任务

• 储备池节点数：节点数越大，记忆容量也就越大，但是计算量和存储的开销也成正比地增加
• 稀疏度：稀疏度过高导致降低状态耦合，记忆能力下降，但是过低会导致状态发散
• 谱半径：谱半径越接近 1，记忆能力越强，但是稳定性越差，谱半径过小会导致状态快速衰减，导致记忆变短
• 正则化参数：正则化参数增大可避免过拟合，但是会降低模型的拟合能力，需要通过交叉验证选择

Leaky ESN

Leaky ESN 是经典 ESN 的一个变体，专门用于处理时间常数变化缓慢或具有非平稳特性的时间序列数据。核心思想就是为神经元的状态更新引入一个泄漏率，可以看作是一个低通滤波器，动态调整网络对历史状态和当前输入的依赖程度。

Leaky ESN 的整体结构与 ESN 一致，最核心的特点体现在储备池内部状态的更新方程多了一个泄漏积分器神经元的机制，在 Leaky ESN 中储备池在 $t$ 时刻的更新公式变为

$$h(t)=(1-\alpha)h(t-1)+\alpha f(W_ix(t)+Wh(t-1)+b)$$

其中 $\alpha\in(0,1]$ 是泄漏率，是 Leaky ESN 的核心。当 $\alpha=1$ 时，公式退化为经典的 ESN，当 $\alpha\rightarrow0$ 时，网络状态变化非常缓慢，但是能更好的维持历史的信息。参数 $\alpha$ 控制了状态更新的速度，小的 $\alpha$ 让储备池由更长的记忆，能平滑噪声，适合学习变化缓慢的特征，大的 $\alpha$ 让神经元响应速度更快，适合捕捉动态。

Deep ESN

Deep ESN 是 ESN 的架构向深度方向的扩展，通过层级化的储备池来学习时间序列数据中更加丰富和层次化的时空特征。经典的 ESN 只有一个浅层的储备池，而 Deep ESN 的核心就是将多个储备池堆叠起来，形成一个深度架构。较低层的储备池捕捉输入数据中简单的、局部的、快速变化的模式，而较高层的储备池则是基于底层的抽象表示，进一步组合出更复杂、全局的、缓慢变化的模式。Deep ESN 网络的结构如下

• 输入层：接收外部时间序列信号 $x(t)$
• 深层储备池：由多个级联的储备池组成的深度结构，每一层都有自己的权重矩阵和状态向量。在高层的储备池的输入就来自于它的下一层的当前状态
  • 第 1 层 $h^1(t)=f(W^1_ix(t)+W^1_hh^1(t-1)+b^1)$
  • 第 $j$ 层 $h^j(t)=f(W^j_ih^{j-1}(t)+W_h^jh^j(t-1)+b^j)$
• 输出层：从所有层或者最高层的储备池状态中读取信息，生成最终的输出，最终的输出为 $y(t)=W_o[h^1(t),…,h^N(t),x(t)]$ 。其中 $W_o$ 依然是唯一需要训练的权重矩阵

Deep ESN 通过堆叠具有多个层间前馈连接的储备池，构建了一个分层的多时间尺度的动态特征提取器，继承了 ESN 训练简单，高效的核心优势，提升了模型对复杂时序数据的建模能力。

后记

循环神经网络优点就是适合序列建模，可处理变长序列，而且整个模型是循环的共享参数，所以模型的规模不会随着序列的长度增长。但是相对于现在的 Transformer 来说，它是顺序计算的，难以并行计算，训练也比较困难，所以只适合用于短序列或者资源受限的场景中。RNN 及其变体是序列建模的重要基础，但是目前在许多任务中被 Transformer 取代。

就先写这么多吧，后续再补充