LuosBlog
0%

状态估计器

发表于 分类于
本文字数： 6.4k 阅读时长 ≈ 6 分钟
状态估计器的设计，根据系统模型和测量数据来估计系统内部的状态

前言

状态估计是根据可以获取的测量数据估算动态系统内部状态的方法，对系统的输入和输出进行测量而得到的数据只能反映系统的外部特性，而系统的动态规律需要通过内部状态变量来描述，因此状态估计对于系统控制很重要。

状态估计器介绍

状态估计器是控制系统和信号处理中的一个重要组件，用于根据系统的测量数据和数学模型来估计系统的内部状态

主要功能

  • 从带有噪声的观测数据中推断系统的内部状态
  • 当某些状态变量无法直接测量时进行估计
  • 提高系统状态信息的准确性

常见类型

  • 最小二乘估计
  • 卡尔曼滤波器
  • 扩展卡尔曼滤波器
  • 无迹卡尔曼滤波器
  • 粒子滤波器
  • Luenberger 观测器

最小二乘估计

基本最小二乘估计

对于线性观测模型

y=Cx+vy=Cx+v

其中 CC 是观测矩阵， vv 是观测噪声， xx 是待估计状态。最小二乘法状态估计就是找到 xx 的最优估计 x^\hat{x} 以最小化残差平方和

J(x)=∥y−Cx∥2=(y−Cx)T(y−Cx)J(x)=\Vert y-Cx\Vert^2=(y-Cx)^T(y-Cx)

对上述代价函数求导并令其梯度为 0，即最小化残差平方和，得到

∂J∂x=−2CT(y−Cx)=0⇓CTy=CTCx^\frac{\partial J}{\partial x}=-2C^T(y-Cx)=0\\\Downarrow\\C^Ty=C^TC\hat{x}

若 CC 可逆，则

x^=(CTC)−1CTy\hat{x}=(C^TC)^{-1}C^Ty

若噪声 vv 的均值为 0，则 E[x^]=xE[\hat{x}]=x ，在高斯噪声下，最小二乘估计是最大似然估计

加权最小二乘估计

假设观测噪声的协方差矩阵 R=E[vvT]R=E[vv^T] 已知，通过加权优化提升估计精度

J(x)=(y−Cx)TR−1(y−Cx)=yTR−1y−yTR−1Cx−xTCTR−1y+xTCTR−1CxJ(x)=(y-Cx)^TR^{-1}(y-Cx)\\=y^TR^{-1}y-y^TR^{-1} Cx-x^TC^TR^{-1}y+x^TC^TR^{-1}Cx

对上述代价函数求导并令其梯度为 0，最小化残差平方和

∂J∂x=−2yTR−1C+2xTCTR−1C=0⇓yTR−1C=xTCTR−1C\frac{\partial J}{\partial x}=-2y^TR^{-1}C+2x^TC^TR^{-1}C=0\\\Downarrow\\y^TR^{-1}C=x^TC^TR^{-1}C

若 CTR−1CC^TR^{-1}C 可逆，则可以得到

x^=(CTR−1C)−1CTR−1y\hat{x}=(C^TR^{-1}C)^{-1}C^TR^{-1}y

如果要使用一段时间内的所有测量值，就需要将 CC 矩阵变得很大，这会占用比较大的空间，也降低了运算的速率

递归最小二乘估计

可以用于在线实时估计，逐次更新状态估计，对于离散线性观测模型

yk=Cx+vky_k=Cx+v_k

在更新 xkx_k 时，添加一个低通滤波器，用于过滤观测噪声，即

x^k=(1−ak)x^k−1+akC−1yk=x^k−1+akC−1(yk−Cx^k−1)⇓x^k=x^k−1+Kk(yk−Cx^k−1)\hat{x}_k=(1-a_k)\hat{x}_{k-1}+a_kC^{-1}y_k=\hat{x}_{k-1}+a_kC^{-1}(y_k-C\hat{x}_{k-1})\\\Downarrow\\\hat{x}_k=\hat{x}_{k-1}+K_k(y_k-C\hat{x}_{k-1})

在递归的过程中通过最小化误差值来不断更新 aa 的值，即可使观测值接近真实值，定义 kk 时刻的误差值为

εk=x−x^k=x−x^k−1−Kk(Cx+vk−Cx^k−1)=(I−KkC)εk−1−Kkvk\varepsilon_k=x-\hat{x}_k\\=x-\hat{x}_{k-1}-K_k(Cx+v_k-C\hat{x}_{k-1})\\=(I-K_kC)\varepsilon_{k-1}-K_kv_k

定义在 kk 时刻的协方差矩阵 Pk=E(εkεkT)P_k=E(\varepsilon_k\varepsilon_k^T) ，为对称矩阵，且对角项是各个误差的方差，在 kk 时刻的误差的平方和就是矩阵 PkP_k 的迹

Jk=E(εkTεk)=tr(Pk)J_k=E(\varepsilon_k^T\varepsilon_k)=tr(P_k)

将矩阵 PkP_k 展开

Pk=E(εkεkT)=E([(I−KkC)εk−1−Kkvk][(I−KkC)εk−1−Kkvk]T)=(I−KkC)E(εk−1εk−1T)(I−KkC)T−(I−KkC)E(εk−1vkT)KkT−KkE(vkεk−1T)(I−KkC)T+KkE(vkvkT)KkTP_k=E(\varepsilon_k\varepsilon_k^T)\\=E([(I-K_kC)\varepsilon_{k-1}-K_kv_k][(I-K_kC)\varepsilon_{k-1}-K_kv_k]^T)\\=(I-K_kC)E(\varepsilon_{k-1}\varepsilon_{k-1}^T)(I-K_kC)^T-(I-K_kC)E(\varepsilon_{k-1}v_{k}^T)K_k^T-K_kE(v_k\varepsilon_{k-1}^T)(I-K_kC)^T+K_kE(v_kv_k^T)K_k^T

由于 εk−1\varepsilon_{k-1} 与 vkv_k 相互独立，且都是零均值噪声，则有

E(εk−1vkT)=E(εk−1)E(vkT)=0E(vkεk−1T)=E(vk)E(εk−1T)=0E(\varepsilon_{k-1}v_{k}^T)=E(\varepsilon_{k-1})E(v_{k}^T)=0\\E(v_k\varepsilon_{k-1}^T)=E(v_k)E(\varepsilon_{k-1}^T)=0

所以上式可以化简为

Pk=(I−KkC)Pk−1(I−KkC)T+KkRKkTP_k=(I-K_kC)P_{k-1}(I-K_kC)^T+K_kRK_k^T

将代价函数对 KkK_k 求导，得到最优的 KkK_k 使得 JkJ_k 取得最小值，此时的 xkx_k 为最优值

∂Jk∂Kk=∂tr(Pk)∂Kk=∂[(I−KkC)Pk−1(I−KkC)T+KkRKkT)]∂Kk=2(KkC−I)Pk−1CT+2KkR=0\frac{\partial J_k}{\partial K_k}=\frac{\partial tr(P_k)}{\partial K_k}=\frac{\partial[(I-K_kC)P_{k-1}(I-K_kC)^T+K_kRK_k^T)]}{\partial K_k}\\=2(K_kC-I)P_{k-1}C^T+2K_kR=0

可以求得 KkK_k 的最优值为

Kk=Pk−1CT(CPk−1CT+R)−1K_k=P_{k-1}C^T(CP_{k-1}C^T+R)^{-1}

总结公式为

x^k=x^k−1+Kk(yk−Cx^k−1)Kk=Pk−1CT(CPk−1CT+R)−1Pk=(I−KkC)Pk−1(I−KkC)T+KkRKkTP0x^0\hat{x}_k=\hat{x}_{k-1}+K_k(y_k-C\hat{x}_{k-1})\\K_k=P_{k-1}C^T(CP_{k-1}C^T+R)^{-1}\\P_k=(I-K_kC)P_{k-1}(I-K_kC)^T+K_kRK_k^T\\P_0\\\hat{x}_0

可以看出，当 Pk−1P_{k-1} 越大时，相应的 KkK_k 越大，而更新过程中也就越相信新得到的值。所以在初始化 P0P_0 和 x^0\hat{x}_0 时，需要选择合适的 P0P_0 来决定对最初的观测值的信任程度

非线性最小二乘估计

当观测模型为非线性的话，需要线性化或者迭代求解，也就是每次从系统中获取到观测值 yy 时，都需要对其进行迭代求解出系统的状态值 xx ，需要注意这里跟递归最小二乘不一样，容易混淆。对于非线性观测模型

y=f(x)+vy=f(x)+v

定义其代价函数，最小化加权残差平方和

J=12(y−f(x))TR−1(y−f(x))J=\frac{1}{2}(y-f(x))^TR^{-1}(y-f(x))

由于 f(x)f(x) 非线性，所以无法直接求出解析解，所以采取迭代的方式求解。有三种求解方法：梯度下降法（收敛速度慢）、牛顿法（需要计算 Hessian 矩阵，计算成本高）和高斯牛顿法

这里使用高斯牛顿法，首先需要计算函数 f(x)f(x) 的雅可比矩阵

jk=∂fx∣x=x^kj_k=\frac{\partial f}{x}\vert_{x=\hat{x}_k}

在当前估计点处对 f(x)f(x) 进行一阶泰勒展开

f(x)=f(x^k)+jk(x−x^k)f(x)=f(\hat{x}_k)+j_k(x-\hat{x}_k)

并且将残差 r(x)=y−f(x)r(x)=y-f(x) 近似为

r(x)≈r(x^k)−jkΔxkr(x)\approx r(\hat{x}_k)-j_k\Delta x_k

将上述的代价函数可以近似为

J=12(r(x^k)−jkΔxk)TR−1(r(x^k)−jkΔxk)J=\frac{1}{2}(r(\hat{x}_k)-j_k\Delta x_k)^TR^{-1}(r(\hat{x}_k)-j_k\Delta x_k)

对 Δxk\Delta x_k 求导，最小化代价函数

∂J∂Δxk=−jkTR−1(r(x^k)−jkΔxk)=0⇓jkTR−1jkΔxk=jkTR−1r(x^k)Δxk=Hk−1gk\frac{\partial J}{\partial \Delta x_k}=-j_k^TR^{-1}(r(\hat{x}_k)-j_k\Delta x_k)=0\\\Downarrow\\j_k^TR^{-1}j_k\Delta x_k=j_k^TR^{-1}r(\hat{x}_k)\\\Delta x_k=H_k^{-1}g_k

其中 HkH_k 为近似 Hessian 矩阵， gkg_k 为梯度，然后进行参数更新，其中 α\alpha 为步长，直到当 Δxk\Delta x_k 足够小时停止

x^k+1=x^k+αΔxkα∈(0,1]\hat{x}_{k+1}=\hat{x}_k+\alpha\Delta x_k\quad\alpha\in(0,1]

但是如果 jkTjkj_k^Tj_k 病态，则需要正则化，在上述中加入阻尼因子 μ\mu

Δxk=(jkTR−1jk+μI)−1jkTR−1r(x^k)\Delta x_k=(j_k^TR^{-1}j_k+\mu I)^{-1}j_k^TR^{-1}r(\hat{x}_k)

  • 当 μ\mu 较大：接近梯度下降法，收敛速度慢
  • 当 μ\mu 较小：接近高斯牛顿法，收敛快但可能发散

Luenberger 观测器

Luenberger 观测器是一种基于模型的状态估计方法，广泛用于线性系统的状态重构和故障检测。通过系统模型和输出误差反馈来估计不可直接测量的状态变量

对于线性时不变系统，其中 ww 是系统误差和模型误差， vv 是观测误差

x˙=Ax+Bu+wy=Cx+v\dot{x}=Ax+Bu+w\\y=Cx+v

设计一个动态系统，利用观测到的 yy 和设定的系统输入 uu 来估计当前状态，根据观测器的动态方程

x^˙=Ax^+Bu+L(y−Cx^)\dot{\hat{x}}=A\hat{x}+Bu+L(y-C\hat{x})

其中 LL 是观测器增益矩阵，也就是观测器设计目标。定义状态的估计误差 e=x−x^e=x-\hat{x} ，其动态方程为

e˙=x˙−x^˙\dot{e}=\dot{x}-\dot{\hat{x}}

将其带入系统方程和观测器方程，可以得到

e˙=x˙−x^˙=Ax+Bu−(Ax^+Bu+L(y−Cx^))=(A−LC)e\dot{e}=\dot{x}-\dot{\hat{x}}\\=Ax+Bu-(A\hat{x}+Bu+L(y-C\hat{x}))\\=(A-LC)e

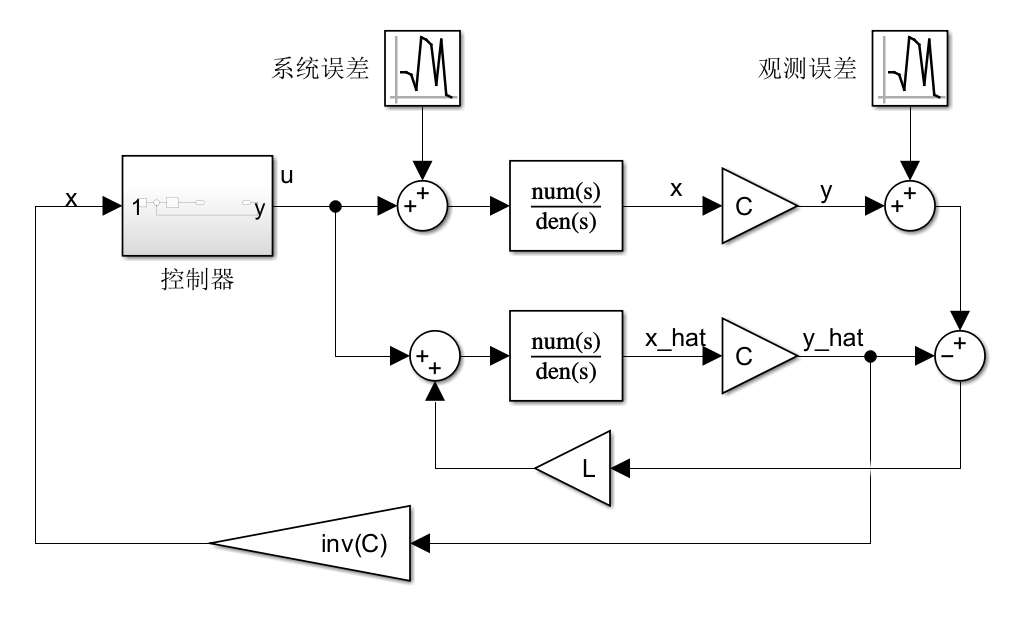
所以设计 LL 使得 A−LCA-LC 的所有特征值都位于左半负平面内，则误差会指数收敛到 0，从而使观测值和实际值误差较小，减小了系统误差和观测误差对系统的影响，最终整个系统的框图如下图所示

1753881064624.png