串联式轮足机器人控制

LQR 控制器设计

参考 双轮足式机器人分析

连杆质心拟合

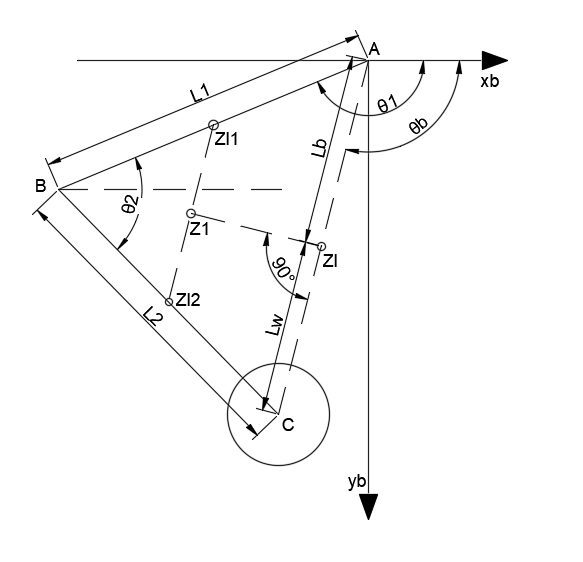
由于在分析和设计控制器的过程中，机器人的腿部连杆需要简化为一个直杆，所以就需要将原来的腿部连杆的转动惯量和质心拟合到虚拟的杆上，如图所示

这里使用机体坐标系，计算可以得到每个杆的坐标位置

$$Z_{l_1}=\begin{bmatrix}l_{1b}\cos\theta_1\\l_{1b}\sin\theta_1\end{bmatrix}\\Z_{l_2}=\begin{bmatrix}l_1\cos\theta_1+l_{2b}\cos(\theta_2+\theta_1-180\degree)\\l_1\sin\theta_1+l_{2b}\sin(\theta_2+\theta_1-180\degree)\end{bmatrix}$$

计算其组合体的质心位置

$$m_1Z_{l_1}+m_2Z_{l_2}=(m_1+m_2)Z_1$$

之后将组合体的质心映射到虚拟杆上，这里直接使用垂足进行映射，是由于点到直线，垂线最短，从而质心映射拟合时产生的误差会最小，联立如下方程求解

$$(\frac{Z_{1y}-Z_{ly}}{Z_{1x}-Z_{lx}})(\frac{C_y-A_y}{C_x-A_x})=-1\\\frac{C_y-Z_{ly}}{C_x-Z_{lx}}=\frac{C_y-A_y}{C_x-A_x}$$

求解即可得到 $Z_l$ 坐标，根据平行轴定理可以得到变换之后的质心处的转动惯量

$$I_l=I_1+m_1(Z_l-Z_{l_1})^T(Z_l-Z_{l_1})+I_2+m_2(Z_l-Z_{l_2})^T(Z_l-Z_{l_2})$$

同时也可以计算出所需要的 $L_w$ 和 $L_b$

$$L_w=\sqrt{(Z_l-C)^T(Z_l-C)}\\L_b=\sqrt{(Z_l-A)^T(Z_l-A)}$$

腿部连杆运动学正解

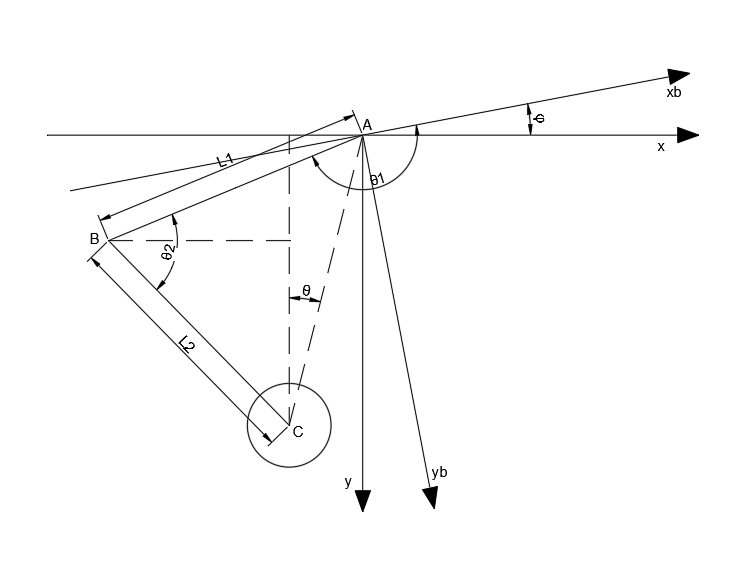
如图所示，首先基于机体坐标系 $x_b-y_b$ 来计算各点的坐标，腿长 $L$ 和腿部摆角角度 $\theta$

$$A_b=\begin{bmatrix}0\\0\end{bmatrix}\\B_b=\begin{bmatrix}l_1\cos\theta_1\\l_1\sin\theta_1\end{bmatrix}\\C_b=\begin{bmatrix}l_1\cos\theta_1+l_2\cos(\theta_2+\theta_1-180\degree)\\l_1\sin\theta_1+l_2\sin(\theta_2+\theta_1-180\degree)\end{bmatrix}$$

利用旋转矩阵将坐标点 $C_b$ 旋转到坐标系 $x-y$ 上，最终计算出来的 $C$ 如下

$$C=\begin{bmatrix}\cos\varphi&\sin\varphi\\-\sin\varphi&\cos\varphi\end{bmatrix}C_b$$

计算腿长 $L$ 和腿部摆动角度 $\theta$ 如下

$$L=\sqrt{C_x^2+C_y^2}\\\theta=\arctan(-\frac{C_x}{C_y})$$

VMC

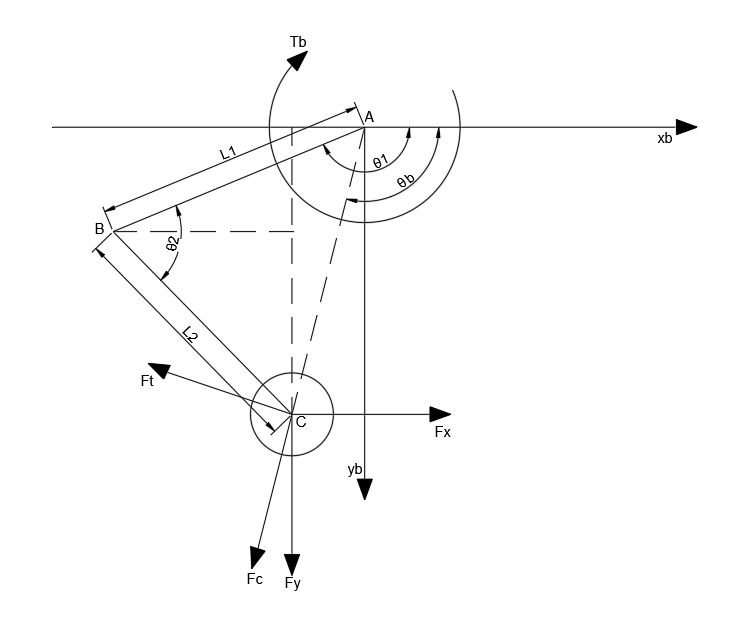
此处采用机体坐标系即 $x_b-y_b$ ，根据上述所计算的 $C_b$ 点计算腿长参数和腿部摆动角 $\theta_b$ ，如下

$$L_b=\sqrt{C_{bx}^2+C_{by}^2}\\\theta_b=\arctan\frac{C_{by}}{C_{bx}}$$

计算其对于 $\theta_1$ 和 $\theta_2$ 的雅各比矩阵

$$\begin{bmatrix}L_b\\\theta_b\end{bmatrix}=J\begin{bmatrix}\theta_1\\\theta_2\end{bmatrix}$$

但是此处求解得到的雅各比矩阵 $J$ 十分复杂，所以将极坐标转换为平行坐标来计算

$$\begin{bmatrix}F_x\\F_y\end{bmatrix}=\begin{bmatrix}\cos\theta_b&-\frac{\sin\theta_b}{L_b}\\\sin\theta_b&\frac{\cos\theta_b}{L_b}\end{bmatrix}\begin{bmatrix}F\\T_b\end{bmatrix}$$

可以将 $C$ 点坐标进行求解雅各比矩阵，得到

$$\begin{bmatrix}\dot{C}_{bx}\\\dot{C}_{by}\end{bmatrix}=\begin{bmatrix}l_2\sin(\theta_1+\theta_2)-l_1\sin\theta_1&l_2\sin(\theta_1+\theta_2)\\l_1\cos\theta_1-l_2\cos(\theta_1+\theta_2)&-l_2\cos(\theta_1+\theta_2)\end{bmatrix}\begin{bmatrix}\dot{\theta}_{1}\\\dot{\theta}_{2}\end{bmatrix}=J\begin{bmatrix}\dot{\theta}_{1}\\\dot{\theta}_{2}\end{bmatrix}$$

由于速度雅可比矩阵是力矩雅各比矩阵的转置，则有

$$\begin{bmatrix}T_1\\T_2\end{bmatrix}=J^T\begin{bmatrix}F_x\\F_y\end{bmatrix}=J^T\begin{bmatrix}\cos\theta_b&-\frac{\sin\theta_b}{L_b}\\\sin\theta_b&\frac{\cos\theta_b}{L_b}\end{bmatrix}\begin{bmatrix}F\\T_b\end{bmatrix}$$

最终化简之后得到

$$\begin{bmatrix}T_1\\T_2\end{bmatrix}=\begin{bmatrix}l_2\sin(\theta_1+\theta_2-\theta_b)-l_1\sin(\theta_1-\theta_b)&\frac{l_1\cos(\theta_1-\theta_b)-l_2\cos(\theta_1+\theta_2-\theta_b)}{L_b}\\l_2\sin(\theta_1+\theta_2-\theta_b)&-\frac{l_2\cos(\theta_1+\theta_2-\theta_b)}{L_b}\end{bmatrix}\begin{bmatrix}F\\T_b\end{bmatrix}$$

反向 VMC 如下

$$\begin{bmatrix}F\\T_b\end{bmatrix}=\begin{bmatrix}\frac{\cos(\theta_1+\theta_2-\theta_b)}{l_1\sin(\theta_2)}&\frac{l_1\cos(\theta_1-\theta_b)-l_2\cos(\theta_1+\theta_2-\theta_b)}{l_1l_2\sin(\theta_2)}\\\frac{L_b\sin(\theta_1+\theta_2-\theta_b)}{l_1\sin(\theta_2)}&\frac{L_bl_1\cos(\theta_1-\theta_b)-L_bl_2\sin(\theta_1+\theta_2-\theta_b)}{l_1l_2\sin(\theta_2)}\end{bmatrix}\begin{bmatrix}T_1\\T_2\end{bmatrix}$$

腿部摆角补偿

由于串联轮腿的腿部质量并不是前后大致均匀分布的，所以需要加一个补偿，可以是 $\theta$ 的补偿，也可以是机体俯仰角 $pitch$ 的补偿，但是如果机体质心位置位于转动关节的上的话，就需要使用 $\theta$ 补偿，另外 $pitch$ 角的补偿导致上层平台并不能保证水平，所以这里只使用 $\theta$ 补偿

$\theta$ 补偿实际就是通过为目标 $\theta$ 添加一个前馈，使整个机器人的重心位于轮子的正上方，否则机器人由于重力与地面的支持力不在同一直线上时，会出现一个倾覆力矩，从而影响机器人的平衡性，如图所示

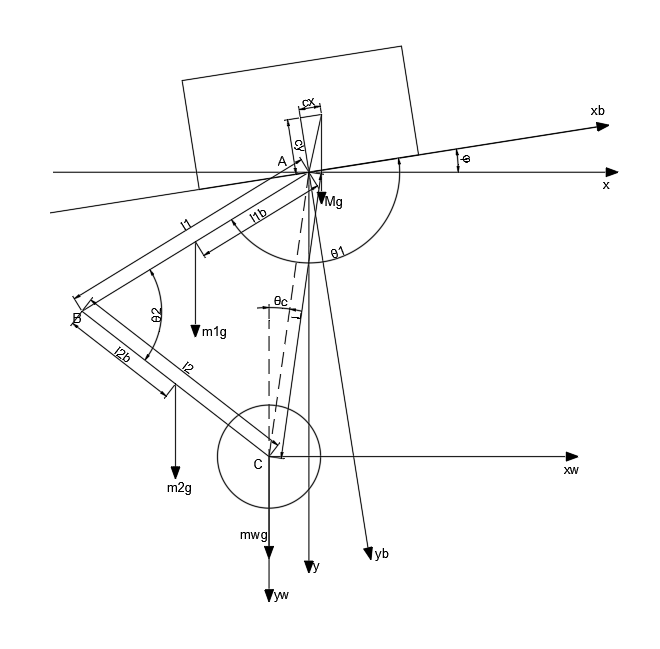
首先分析在机器人坐标系中，可以得到机器人各个部分重心的位置

$$Z_b=\begin{bmatrix}c_x\\-c_y\end{bmatrix}\\Z_{l_1}=\begin{bmatrix}l_{1b}\cos\theta_1\\l_{1b}\sin\theta_1\end{bmatrix}\\Z_{l_2}=\begin{bmatrix}l_1\cos\theta_1+l_{2b}\cos(\theta_2+\theta_1-180\degree)\\l_1\sin\theta_1+l_{2b}\sin(\theta_2+\theta_1-180\degree)\end{bmatrix}\\Z_w=\begin{bmatrix}l_1\cos\theta_1+l_2\cos(\theta_2+\theta_1-180\degree)\\l_1\sin\theta_1+l_2\sin(\theta_2+\theta_1-180\degree)\end{bmatrix}$$

将上述重心坐标转移到轮子坐标系 $x_w-y_w$ 中，得到

$$Z_b=\begin{bmatrix}\cos\varphi&\sin\varphi\\-\sin\varphi&\cos\varphi\end{bmatrix}\begin{bmatrix}c_x\\-c_y\end{bmatrix}+\begin{bmatrix}L\sin\theta_c\\-L\cos\theta_c\end{bmatrix}\\Z_{l_1}=\begin{bmatrix}\cos\varphi&\sin\varphi\\-\sin\varphi&\cos\varphi\end{bmatrix}\begin{bmatrix}l_{1b}\cos\theta_1\\l_{1b}\sin\theta_1\end{bmatrix}+\begin{bmatrix}L\sin\theta_c\\-L\cos\theta_c\end{bmatrix}\\Z_{l_2}=\begin{bmatrix}\cos\varphi&\sin\varphi\\-\sin\varphi&\cos\varphi\end{bmatrix}\begin{bmatrix}l_1\cos\theta_1+l_{2b}\cos(\theta_2+\theta_1-180\degree)\\l_1\sin\theta_1+l_{2b}\sin(\theta_2+\theta_1-180\degree)\end{bmatrix}+\begin{bmatrix}L\sin\theta_c\\-L\cos\theta_c\end{bmatrix}\\Z_w=0$$

假定此时的 $\theta_c$ 正好满足要求，此时根据重心公式可以得到

$$MZ_{bx}+m_1Z_{l_1x}+m_2Z_{l_2x}=0$$

求解可以得到 $\theta$ 的补偿角度

$$\theta_c=-\arcsin\frac{(m_1l_{1b}+m_2l_1)\cos(\varphi-\theta_1)-m_2l_{2b}\cos(\theta_1+\theta_2-\varphi)+M(c_x\cos\varphi-c_y\sin\varphi)}{L(M+m_1+m_2)}$$

在使用时可以直接添加到当前状态中，即状态空间方程变为

$$X=\begin{bmatrix}\theta-\theta_c\\\dot{\theta}\\x\\\dot{x}\\\varphi\\\dot\varphi\end{bmatrix}$$