拉普拉斯变换
拉普拉斯变换
一个定义在区间 [0,∞) 的函数 f(t) ,它对应的拉普拉斯变换 F(s) 定义为
F(s)=∫0∞f(t)e−stdt
F(s) 称为 f(t) 的象函数,而 f(t) 称为 F(t) 的原函数,这个变换过程通常记作 F(s)=L[f(t)]
拉普拉斯逆变换
拉普拉斯逆变换就是已知上述的 F(s) 求解 f(t) 的过程,公式如下
f(t)=2πj1∫β−j∞β+j∞F(s)estds
记作 f(t)=L−1[F(s)]
对于比较复杂的 F(s) 来说,拉普拉斯逆变换并不容易求解,所以一般会将 F(s) 进行因式分解为 (s−p)r1 的形式再进行求解
根轨迹
根轨迹的介绍
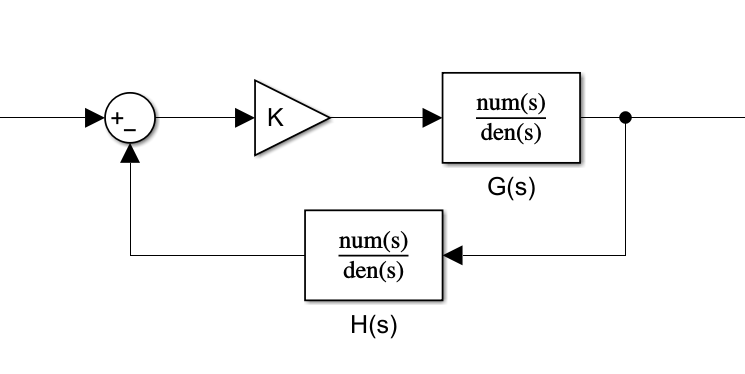
上述系统中的闭环传递函数为
Φ(s)=1+KG(s)H(s)KG(s)
而根轨迹是指当系统开环的某个参数从零变化到无穷大时,闭环传递函数的极点(实际上就是分母为 0 时的根)在复平面上移动的轨迹,实际上就是通过研究开环传递函数 G(s)H(s) 来得到 1+KG(s)H(s)=0 的根的移动轨迹。它所对应的根轨迹图如下图所示
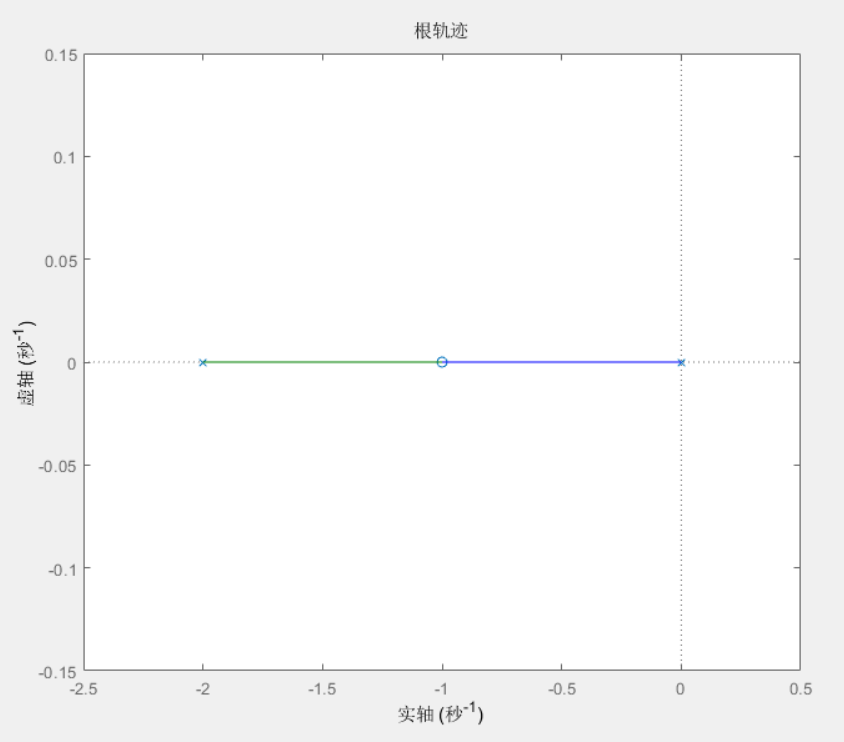
根轨迹的绘制
对于上述的传递函数,我们对 G(s)H(s) 进行研究,一般会将其进行因式分解,表示为如下的形式
G(s)H(s)=(s−p1)(s−p2)⋯(s−pn)(s−z1)(s−z2)⋯(s−zm)
- z1,…zm 就是零点,共有 m 个零点,即为 m 阶的,并且在图中用 ⚪ 来表示
- p1,…pn 是极点,共有 n 个极点,即为 n 阶的,在图中用 × 表示
虽然在 matlab 中只需要一条指令 rlocus(G) 就能绘制根轨迹,但是为了便于观察根轨迹的运行规律,还是要介绍一下绘制规则
- 一共有 max(n,m) 条根轨迹
- 当 n=m 时,随着 K 从 0 到正无穷,根轨迹从其零点移动到其极点
- 实轴上的根轨迹存在于从右向左数第奇数个零/极点的左边
- 若复数根存在,那它一定是共轭的,所以根轨迹通过实轴对称
- 若 n>m ,则有 n−m 个极点指向无穷
- 若 n<m ,则有 m−n 条根轨迹从无穷指向零点
- 根轨迹沿着渐近线移动,而渐近线与实轴的交点为 σ=n−m∑pi−∑zi ,渐近线与实轴的夹角为 θ=n−m2q+1πq=0,1,...n−m−1(m−n−1)
- 根轨迹的汇合点和分离点,由特征方程 1+KG(s)H(s)=0 求解得到 K=−G(s)H(s)1 ,对 K 关于 s 求导,并令导数等于 0,即 dsdK=0 ,求解得到的实数即为分离点或汇合点
- 汇合点是指根轨迹从复平面返回实轴的点
- 分离点是指根轨迹从实轴上分离并进入复平面的点
根轨迹与系统性能

- 稳定性
- 若所有极点位于复平面的左半部分,系统稳定
- 若有极点位于右半部分,系统不稳定
- 动态响应
- 超调量:极点距离虚轴越近,阻尼越小,超调量越大
- 调节时间:极点离虚轴越远,调节时间越短
- 震荡频率:极点的虚部越大,震荡频率越高
- 如果特征方程的根为复数 s=σ±jw
- 复数极点的实部 σ 决定了系统的收敛速度和调节时间
- 复数极点的虚部 w 决定了系统的震荡频率
- 主导极点:靠近虚轴的极点对系统响应起主导作用,远离虚轴的极点影响较小,若存在一对共轭复数主导极点,系统的动态响应主要由这对极点决定
- 通过调整增益 K 可以使得系统具有较小的超调量,较短的调节时间和较高的稳定性
- 随着 K 不断增大,根从极点移动到零点的位置,就是闭环传递函数极点的位置,然后经过判断闭环传递函数的极点位置来判断系统的稳定性
- 对于在根轨迹上的点,满足 ∠KG(s)H(s)=−π(2q+1)q=0,±1,... ,也就是该点到零点的夹角和减去该点到极点的夹角和
- 对于在根轨迹上的点,满足 ∣KG(s)H(s)∣=1=K∏lp∏lz ,后面那一项就是该点到所有零点的距离之积除以该点到所有极点的距离之积
奈奎斯特稳定判据
柯西辐角原理
假设 f(x) 是一个闭合路径 C 上解析且无零点的复变函数,且在 C 内除有限个极点和零点外解析,则柯西辐角原理可以表述为
2π1△Cargf(s)=Z−P
- △Cargf(s) 是函数 f(s) 的辐角 f(s) 的辐角沿闭合路径 C 的变化量
- Z 是函数 f(s) 在 C 内的零点个数
- P 是函数 f(s) 在 C 内的极点个数
在 S 平面内顺时针画一条闭合曲线 A,而 B 曲线是 A 通过 f(s) 后再 f(s) 平面上的映射,A 曲线每包含一个 f(s) 的零点,B 曲线就绕着 (0,0) 顺时针绕一圈,A 曲线每包含一个 f(s) 的极点,B 曲线就绕着 (0,0) 逆时针绕一圈
奈奎斯特图

奈奎斯特稳定判据(Nyquist Stability Criterion)是控制理论中用于分析闭环系统稳定性的一种重要方法,通过分析开环传递函数 KG(s)H(s) 的频率响应即奈奎斯特图,判断闭环系统传递函数 1+KG(s)H(s)KG(s) 的稳定性
对上述方程进行分析可知, KG(s)H(s) 的极点就是 1+KG(s)H(s) 的极点, 1+KG(s)H(s) 的零点就是闭环传递函数 1+KG(s)H(s)KG(s) 的极点
柯西辐角原理被用于推导奈奎斯特稳定判据,具体步骤如下
- 对于闭环系统的特征方程 1+G(s)H(s)=0 ,定义函数 f(s)=1+G(s)H(s)
- 选择闭环路径,选择奈奎斯特路径 C,通常是一个包含整个右半平面的半圆,并分析 G(s)H(s) 在 C 上的行为
- 根据柯西辐角原理, Z 是 f(s) 在右半平面的零点数,即闭环传递函数的不稳定极点数, P 是 f(s) 在右半平面的极点数,即开环传递函数的不稳定极点数
- 通过分析 f(s)=1+G(s)H(s) 的辐角变化,可以推导出奈奎斯特稳定判据 Z=P−N ,其中 N 就是曲线围绕 (0,0) 的包围次数,顺时针绕一圈就减一,逆时针绕一圈就加一
- 将上述 f(s) 函数左右减一,也就是将曲线平移一下,而原来的 Z 和 P 保持不变,得到的这个曲线就是奈奎斯特图
奈奎斯特稳定性判据
由于系统稳定的条件就是闭环传递函数 1+G(s)H(s)G(s) 在复平面的右半边没有极点,也就是 Z=0 ,根据上述得到的 Z=P−N 公式,可以得到奈奎斯特稳定性判据为 P=N
奈奎斯特稳定判据示例
对于下面的系统
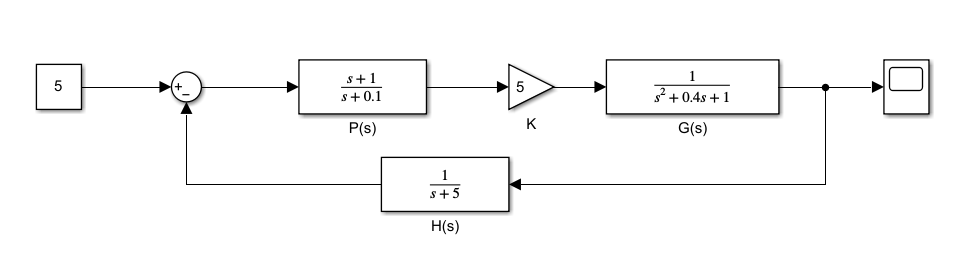
首先当 K=1 时,分析其奈奎斯特图,如下
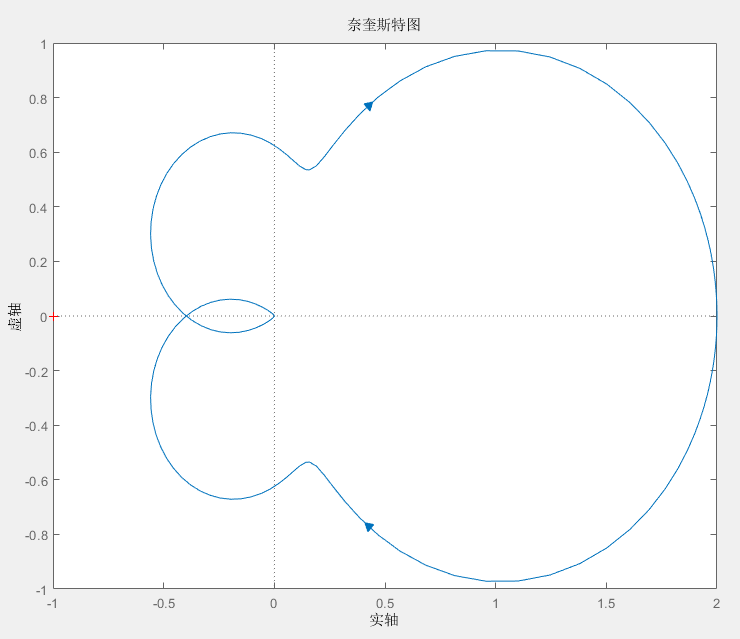
可以看到奈奎斯特图绕 (−1,j0) 点的圈数为 0,而 G(s)H(s) 在右半平面的极点数 P=0 ,计算得到 Z=0 ,所以该系统闭环传递函数在复平面的右半边没有极点,所以系统稳定
当 K=5 时,得到如下红色的奈奎斯特图
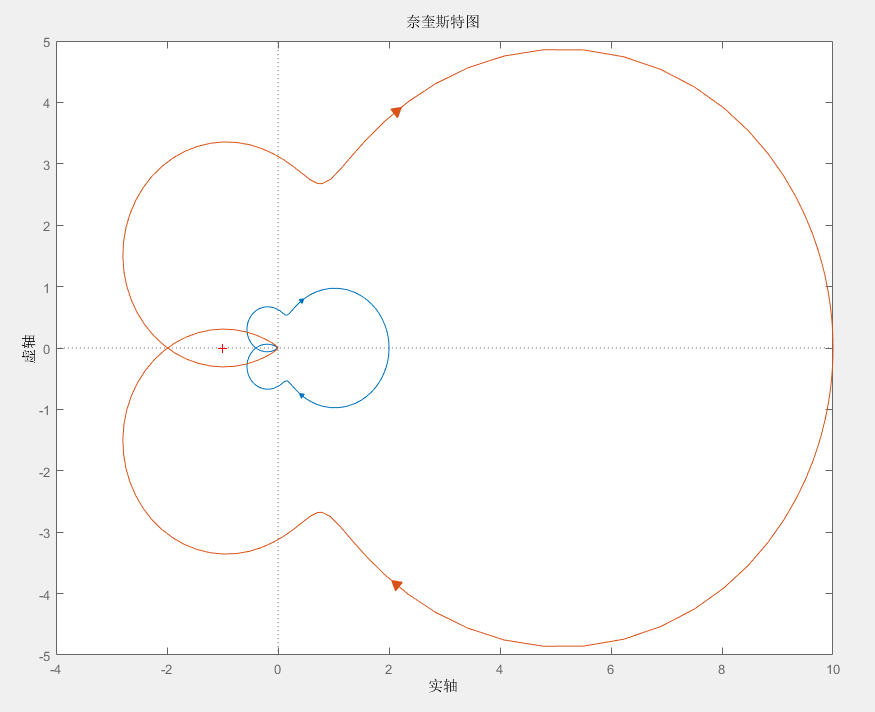
可以看到奈奎斯特图绕 (−1,j0) 点的顺时针圈数为 2,即 N=−2 ,而 G(s)H(s) 在右半平面的极点数 P=0 ,计算得到 Z=2 ,所以该系统闭环传递函数在复平面的右半边有极点,所以系统不稳定
实际的运行图如下所示
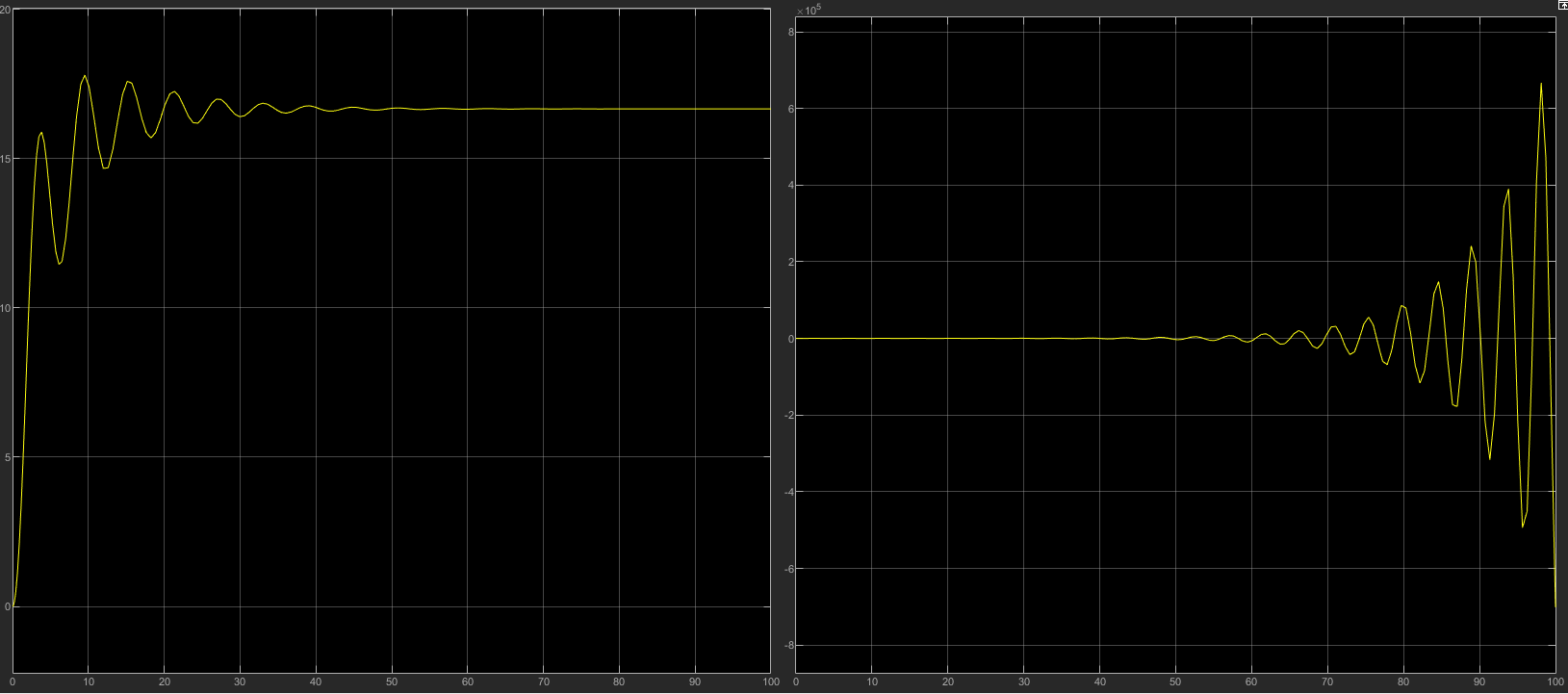
可以看出左边的是 K=1 的运行状态,右边的是 K=5 的运行状态
伯德图
伯德图定义
伯德图是系统频率相应的一种图示方法,伯德图由幅值图和相角图组成,两者都按照频数的对数分度绘制。幅值图的纵轴表示为 20logA 的形式,使用分贝来表示幅值
- 幅频特性图
- 横轴为频率,通常以对数刻度表示
- 纵轴为系统幅值,以分贝形式表示
- 展示系统增益随频率的变化
- 相频特性图
- 横轴为频率,通常以对数刻度表示
- 纵轴为系统相位
- 展示系统相位随频率的变化
伯德图与系统稳定性
闭环系统的稳定性取决于开环传递函数的频率响应,也就需要对伯德图进行分析,通过伯德图可以分析系统的增益裕度和相位裕度来判断系统稳定性
- 增益裕度:在相位达到 −180∘ 处的频率即相位穿越频率 wp ,系统增益与 0dB 之间的差值 GM=0−20log∣G(jwp)∣
- 如果 GM>0dB 系统稳定
- 如果 GM<0dB 系统不稳定
- GM 越大,系统相对稳定性越好
- 相位裕度:在增益达到 0dB 处的频率即增益穿越频率 wg ,系统相位与 −180∘ 的差值 PM=∠G(jwg)−(−180∘)
- 如果 PM>0dB 系统稳定
- 如果 PM<0dB 系统不稳定
- PM 越大,系统相对稳定性越好
即使系统稳定,增益裕度和相位裕度的大小也反映了系统的相对稳定性,一般要求 GM>6dB 且 PM>30∘
伯德图示例
对于一个系统 G(s)=a+sa ,计算其幅频特性和相频特性如下
G(jw)=1+jaw1=1+(aw)2earctan(aw)1⇓∣G(jw)∣=1+(aw)21∠G(jw)=−arctan(aw)
对其进行分析
- w≪a 时 ∣G(jw)∣=1,∠G(jw)=0 计算得到 20log∣G(jw)∣=0
- w=a 时 ∣G(jw)∣=21,∠G(jw)=−45∘ 计算得到 20log∣G(jw)∣=−3dB
- w≫a 时 ∣G(jw)∣=w1,∠G(jw)=−90∘ 计算得到 20log∣G(jw)∣=−20logw
计算可以看出,幅值图中最初斜率为 0,之后大致在 w=a 处会转折,而最终斜率会下降为 −20 ,而相位图中会有 0∘ 和 −90∘ 两条渐近线。设定 a=10 利用 matlab 绘制伯德图如下
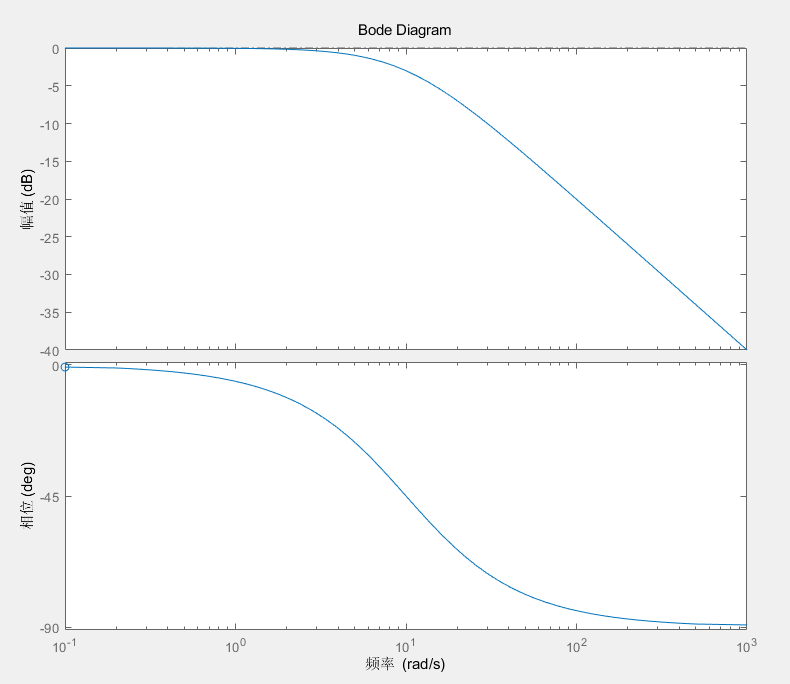
超前补偿器
超前补偿器定义
超前补偿器主要用于提高系统的相位裕度,增强系统的稳定性和响应速度,传递函数形式为
G(s)=s+ps+z∣z∣<∣p∣
超前补偿器特点
- 增加相位裕度,提高系统的稳定性
- 提高系统的响应速度
- 适用于系统相位裕度不足的情况
超前补偿器示例
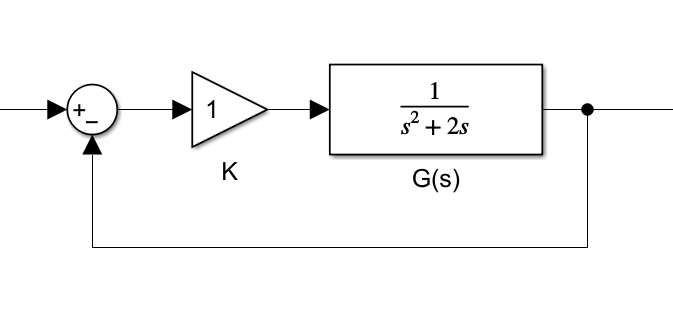
对于一个系统的开环传递函数 G(s)=s2+2ss2+2s+1 ,绘制其根轨迹,如下图所示

可以看到,系统的特征方程的根在 [−2,0] 之间。由上述根轨迹的性质可知,根的实部决定了系统的收敛速度,实部越接近虚轴,收敛速度越慢
所以当想要对这个系统进行调整时,例如想要将 −4+3i 加入到根轨迹中,以此来加快收敛速度。根据上述的在根轨迹上的点满足 ∠KG(s)H(s)=−π(2q+1)q=0,±1,... ,
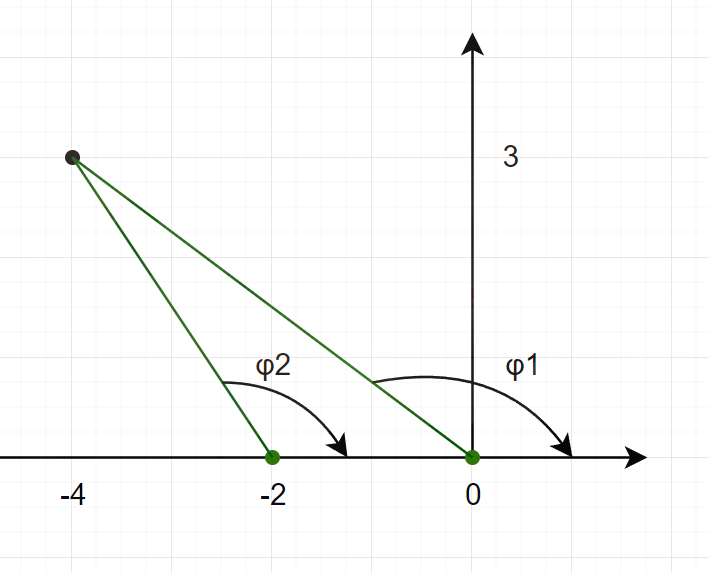
上述图中,使用绿色表示极点,黑色点就是想要加入根轨迹的点,可以得到 ∠KG(s)H(s)=0−(ϕ1+ϕ2)=−1.4823π ,可知这个点并不在根轨迹上,所以要做一些调整
一般来说,可以直接调整零点与该点的夹角为 0.4823π ,计算之后就可以得到零点为 −4.1670 ,所以可以在 G(s) 的基础上增加一个补偿 G1(s)=s+4.1670 ,得到如下的系统
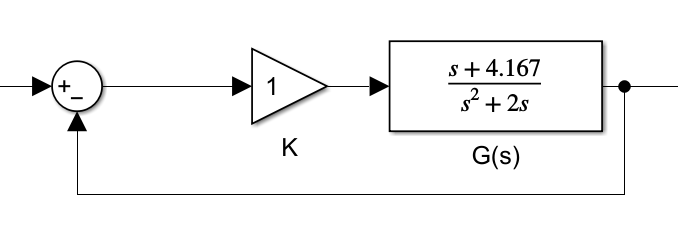
该系统对应的根轨迹为
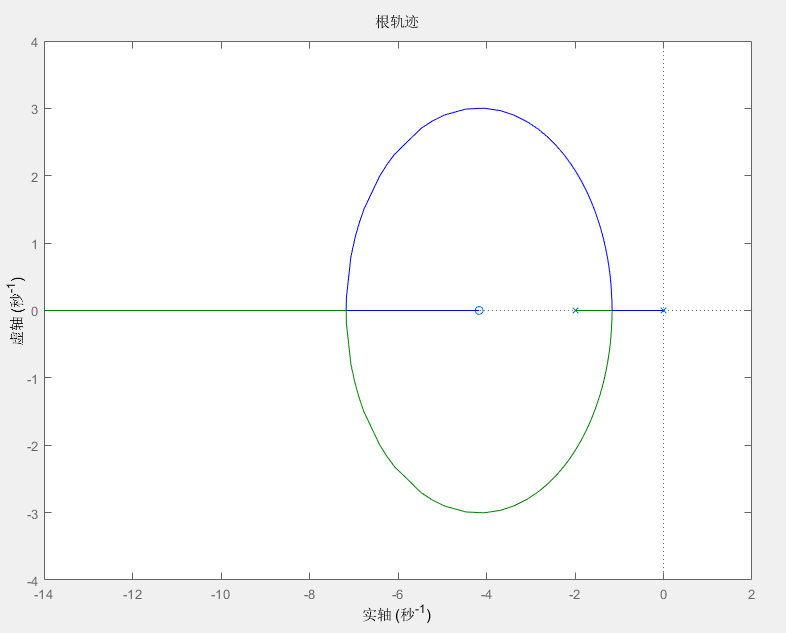
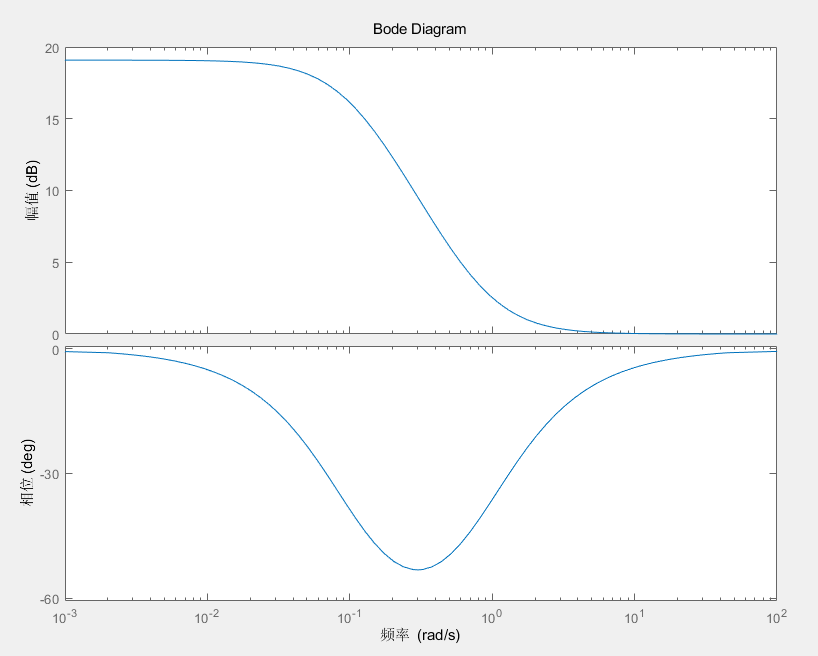
实际上这个 s+4.1670 就是一个 PD 控制器,其中 s 是微分项,4.167 是比例项,其对应的伯德图如下图所示,可以看出随着频率的增加,幅值也不断增加,所以其对高频噪声比较敏感
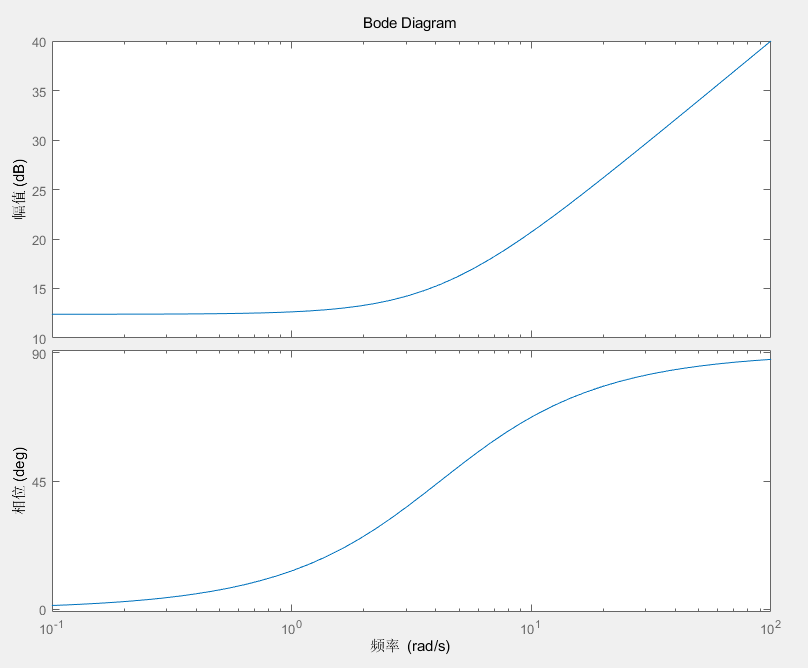
所以需要用到超前补偿器,也就是在调整零点与该点的夹角时也增加一个极点来做调整,也就是可以增加一个零点与其角度为 0.7π 和一个极点与其角度为 0.2177π ,计算之后得到零点和极点为 −1.8204 和 −7.6802 ,也就是添加一个传递为 s+7.6802s+1.8204 ,添加了超前补偿器的系统的根轨迹如图所示
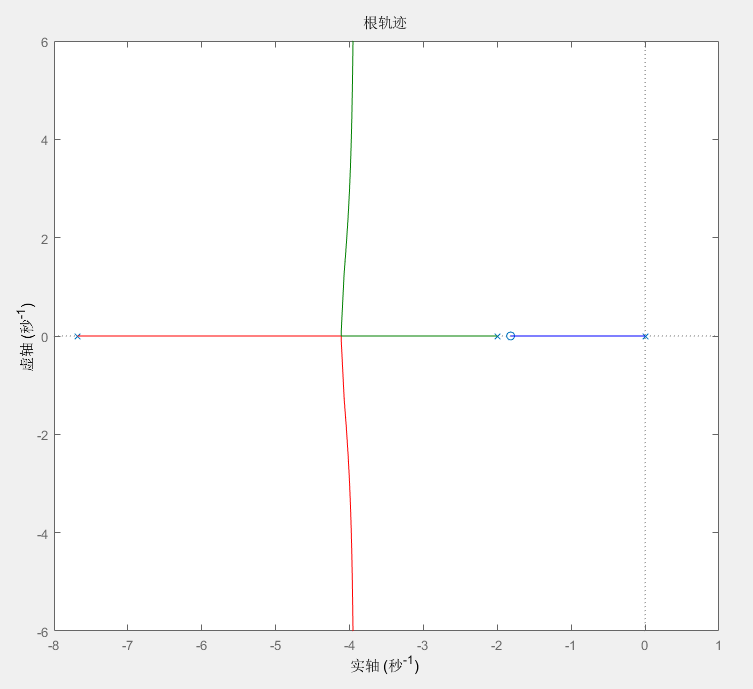
这个补偿器对应的伯德图如下。可以看出来,这个补偿器把相位提前了一部分,就是超前补偿器
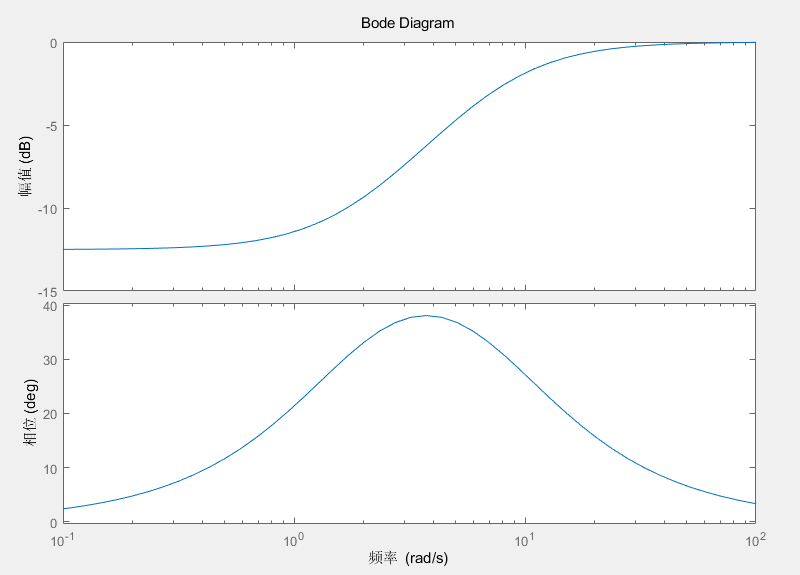
对比添加超前补偿器前后系统的伯德图,如下
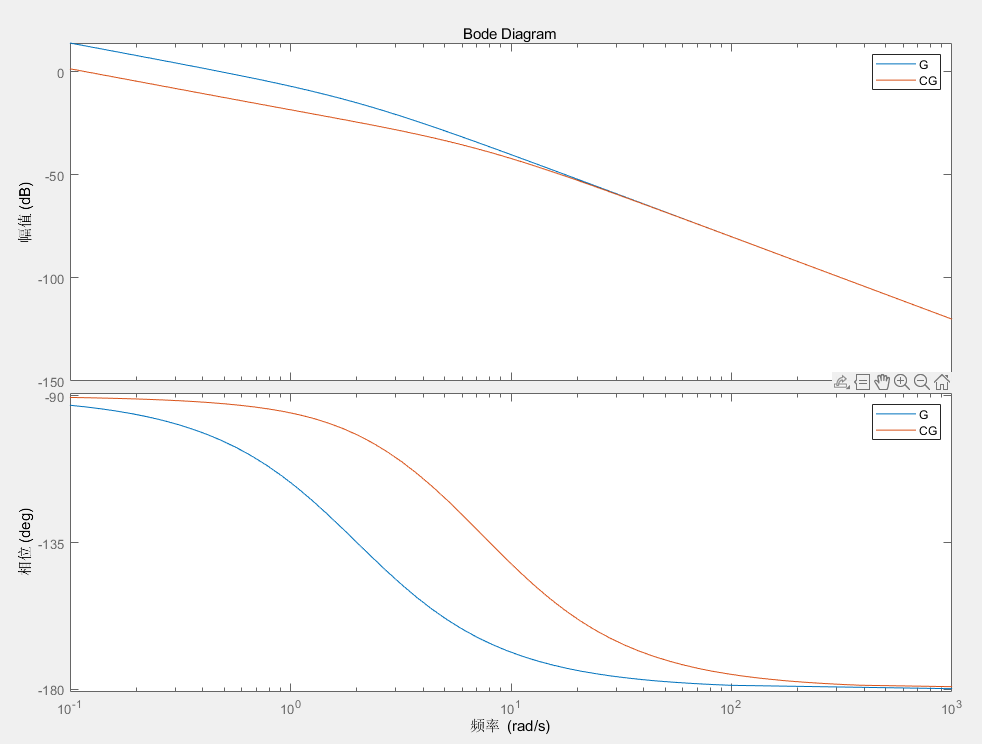
可以看出,超前补偿器增加了原系统的相位裕度,提高了系统的稳定性
滞后补偿器
滞后补偿器定义
滞后补偿器主要用于改善系统的稳态误差,同时保持系统的稳定性。其传递函数形式为
G(s)=s+ps+z∣z∣>∣p∣
滞后补偿器特点
- 改善稳态误差
- 降低高频增益,减少噪声影响
- 适用于系统稳态误差较大时
滞后补偿器示例
对于如下的一个系统
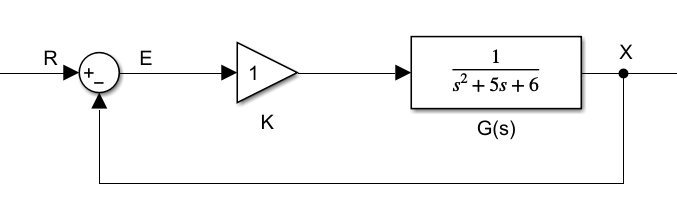
可以求解该系统的传递函数为 1+KG(s)KG(s) 而系统的误差可以表示为 E=R−X ,带入传递函数可以得到
E=1+KG(s)1R
当系统运行到稳定时,可以计算出系统的稳态误差如下,当 K=6 时,稳态误差为 0.5R
E=K+66R
所以可以设计一个滞后补偿器将稳态误差减小,设计补偿器如下
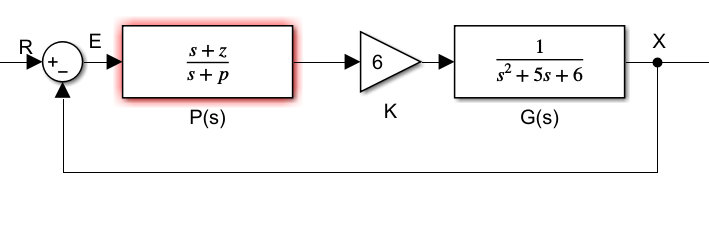
P(s)=s+ps+z
重新计算稳态误差为
E=1+KG(s)P(s)1R=6+Kpz6R
要使稳态误差减小,必须增大 Kpz 项,所以这里设计的滞后补偿器需要 ∣z∣>∣p∣
当 p=0 时, pz→∞ 稳态误差就趋近于 0,这时候将滞后补偿器化简可以得到 P(s)=1+sz ,第一项就是比例项,第二项是积分项,这就是个 PI 控制器,PI 控制器可以将系统的稳定误差控制趋近于 0 的
现在设计补偿器使得误差 E=0.1R ,并且保持 K=6 ,计算之后可以得到 pz=9 ,但是只有一个比例值,具体取值还需要进行判断和调整。可以选取 z=9,p=1 和 z=0.9,p=0.1 进行比较,得到如下的运行结果
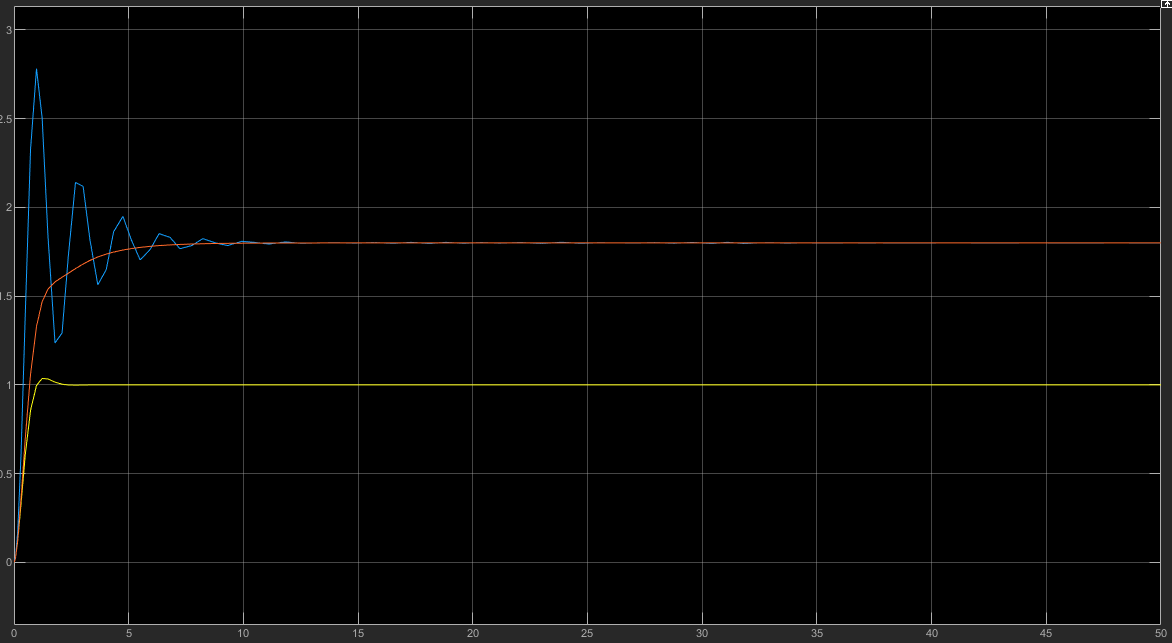
其中蓝色的线就是 z=9,p=1 的情况,而红色的线为 z=0.9,p=0.1 的情况,可以看出红线与黄线的运行轨迹比较相似,而蓝线却很不一样,这里可以从根轨迹来分析这两种情况,如下,第一个是原系统的根轨迹,第二个是 z=9,p=1 的根轨迹,第三个是 z=0.9,p=0.1 的根轨迹
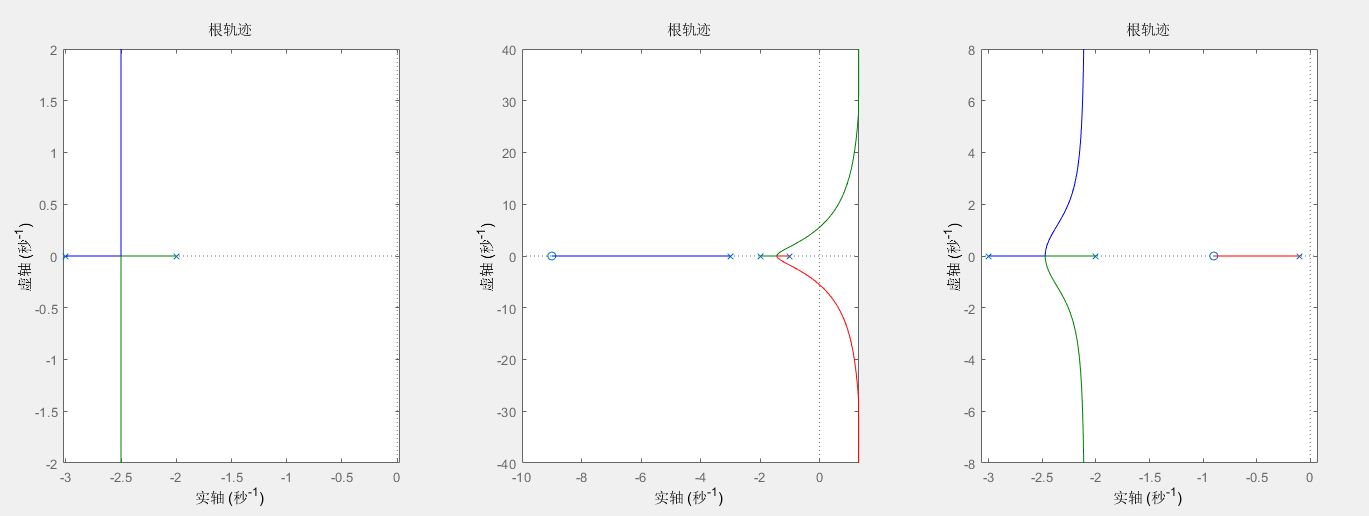
可以发现第二个根轨迹已经与原来的根轨迹相差很多了,这是因为,所有根轨迹上的点满足该点到零点的夹角和减去该点到极点的夹角和为 -180,所以当新增加的零极点相差很小时,它们两个点与根轨迹上点的夹角就很相近,计算的时候就会抵消,从而对原来的根轨迹的影响不大,反之就是导致根轨迹变化很大,从而丢失了系统原来的特性。所以在设计滞后补偿器时,要使得零极点尽量靠近虚轴,这样就算它们差别很大,也不会距离很远,就能尽可能保证系统原有的瞬态响应
而滞后补偿器的伯德图如下所示,这个补偿器把相位滞后了一部分,所以被称为滞后补偿器