轮式底盘解算

四舵轮底盘控制

四舵轮底盘就是由四个舵轮来控制底盘运动的，一般在进行速度分析时，会将底盘的整体运动映射到四个轮子的单独运动上去

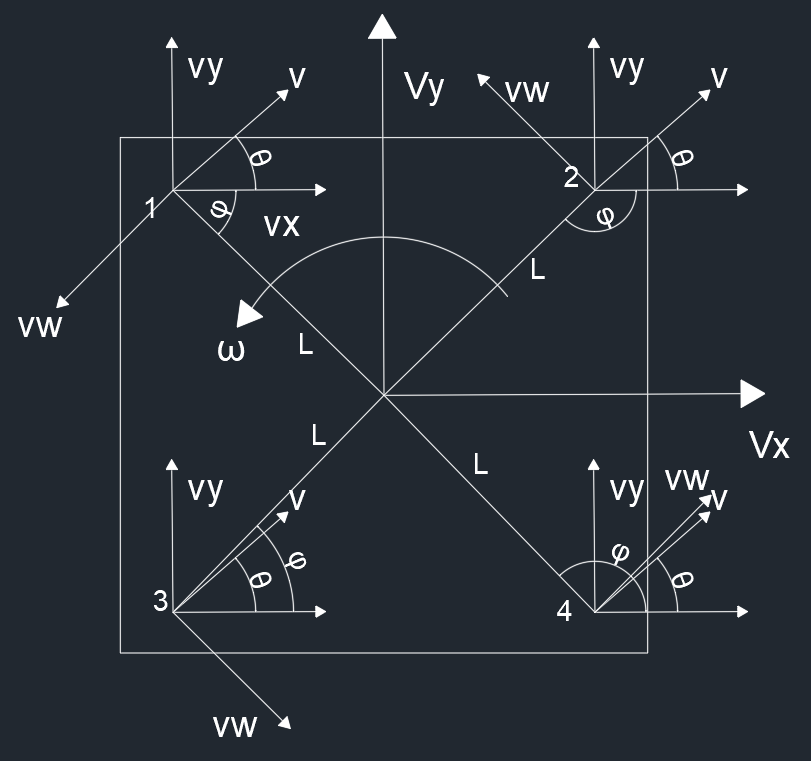
一般来说是将直角坐标的速度和角速度分别映射到轮子上，进行累加得到最终的结果

直角坐标速度分析

直角坐标的速度分析相对来说比较简单，直接就是坐标平移，所以就是

$v_{ixx}=V_x\\v_{ixy}=0\\v_{iyx}=0\\v_{iyy}=V_y\\$

其中 $v_{iyx}$ 就是机体的 $x$ 方向速度向轮子 $y$ 方向速度的映射

角速度分析

角速度分析实际上就是把机体转动的角速度通过轮子的运动来实现，也就是

$v_{iw}=L_iw$

再将其分解到直角坐标系中

$v_{ixw}=wL_i\cos(\varphi-90)\\v_{iyw}=wL_i\sin(\varphi-90)$

其中 $v_{ixw}$ 就是机体角速度向轮子 $x$ 方向速度的映射

最终速度

最终两部分速度相加就是该轮子的速度

$v_{ix}=v_{ixx}+v_{ixy}+v_{ixw}\\v_{iy}=v_{iyx}+v_{iyy}+v_{iyw}$

舵角

得到最终的直角坐标速度之后，还需要得到舵角速度和总速度，主要是因为舵轮的驱动轮只能有一条直线上的速度，而舵角可以来调整这个速度的方向

$\theta_i=\arctan\frac{v_{ix}}{v_{iy}}$

驱动轮速度

$v_i=\sqrt{v_{ix}^2+v_{iy}^2}$

最小舵转角

在舵轮的舵角转动中，需要使得舵角转动按照转动最小的方向转动，以此来防止转动角度太大而导致车身偏斜

直接附上代码，这里就不再解释了

float angleDiff  = aimAngle - wheel->angleNow;    // 转角（过程量）
int   temp       = floor(angleDiff / PI + 0.5f);  // 数形结合，左移1/2个单位，每转90度需要一次最小角反向，0.5即(PI/2)/PI
wheel->angleSet += angleDiff - PI * temp + wheel->angleNow;
if (fabsf(wheel->angleSet) > 4 * PI)
  wheel->angleSet -= sign(wheel->angleSet) * 2 * PI;
wheel->angleSetDeg = wheel->angleSet * RAD_TO_DEG;
return powf(-1.f, temp); // 返回舵轮的速度方向

四全向轮底盘控制

四全向轮底盘控制是由四个全向轮控制的，只能控制轮子方向的速度而不能控制轮子垂直方向的速度，所以在分析时只考虑轮子方向的速度

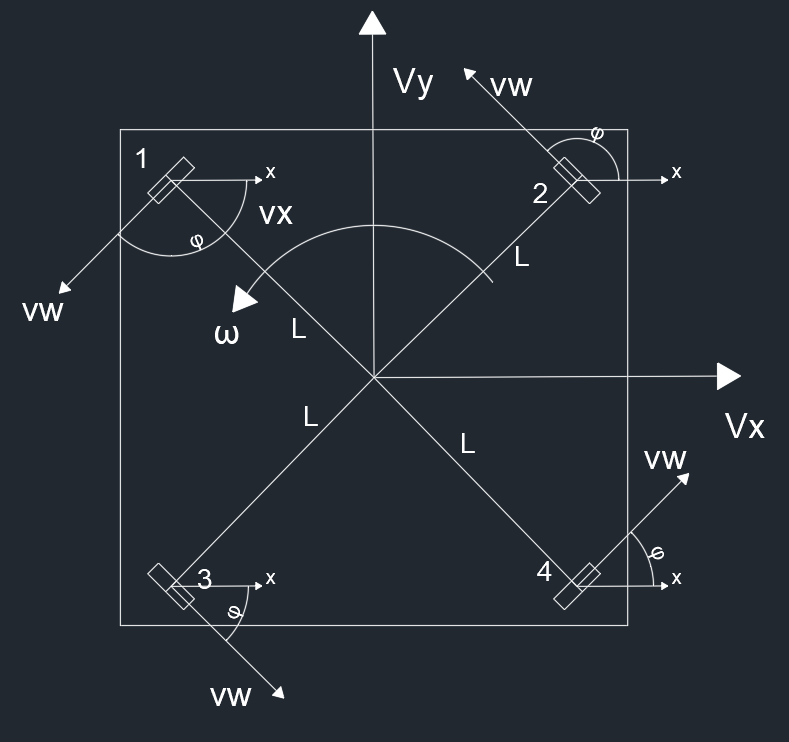
同四舵轮底盘一致，将直角坐标的速度和角速度分别映射到轮子上，进行累加得到最终的结果

直角速度分析

如图，轮子的直角坐标系的速度就是底盘的直角坐标系速度，所以可以得到

$v_{ixx}=V_x\\v_{ixy}=0\\v_{iyx}=0\\v_{iyy}=V_y\\$

其中 $v_{iyx}$ 就是机体的 $x$ 方向速度向轮子 $y$ 方向速度的映射

角速度分析

底盘的角速度映射到轮子的线速度可以得到

$v_{iw}=L_iw$

一般来说，这里算出来的角速度方向会与舵轮轮子前进方向一致，当然也有将底盘安装为长方形的底盘，这时就将这个速度 $v_{iw}$ 与实际轮子前进方向的夹角定为 $\theta_i$

$v_{iw}=v_{iw}\cos\theta$

最终速度

最终速度就是上述两个速度的和，并且需要映射到轮子前进方向上，所以

$v_i=v_{iw}+(v_{ixx}+v_{iyx})\cos\varphi+(v_{ixy}+v_{iyy})\sin\varphi$

在垂直于轮子的方向上不考虑

麦克纳姆轮控制

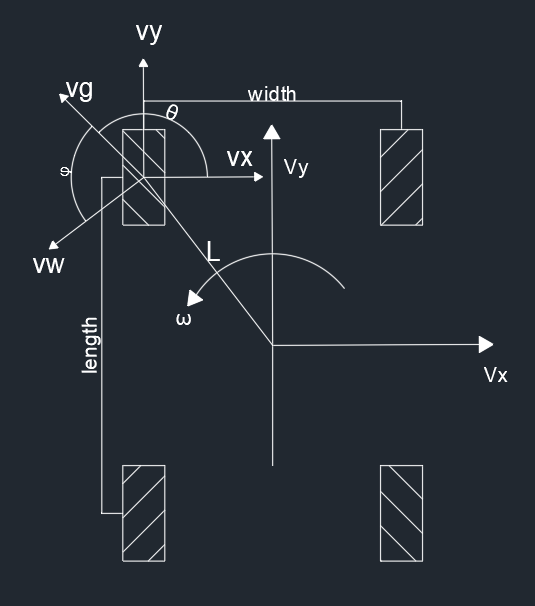
首先先来说说麦克纳姆轮的特点：有辊子，并且辊子与轮子角度成 45 度角。而且对于自由的辊子来说，无法控制辊子转动方向的速度，所以只能控制沿着辊子方向的速度来控制轮子转动的速度了，所以也就是分析轮子时需要将速度映射到辊子方向上

直角坐标速度分析

如图，轮子的直角坐标系的速度就是底盘的直角坐标系速度，所以可以得到

$v_{ixx}=V_x\\v_{ixy}=0\\v_{iyx}=0\\v_{iyy}=V_y\\$

其中 $v_{iyx}$ 就是机体的 $x$ 方向速度向轮子 $y$ 方向速度的映射

角速度分析

底盘的角速度映射到轮子的线速度可以得到

$v_{iw}=L_iw$

最终速度

将上述速度映射到辊子方向上，可以得到

$v_{ig}=v_{iw}\cos\varphi+(v_{iyy}+v_{ixy})\sin\theta+(v_{ixx}+v_{iyx})\cos\theta$

最终辊子方向上的速度映射到轮子转动方向，也就是

$v_{i}=\frac{v_{ig}}{\sin\theta}$

最终得到的就是轮子需要转动的速度

注意

这个控制是根据笔者的想法推导出来的，并非是真实实验的结果，所以不一定正确，注意辨别

三舵轮底盘控制

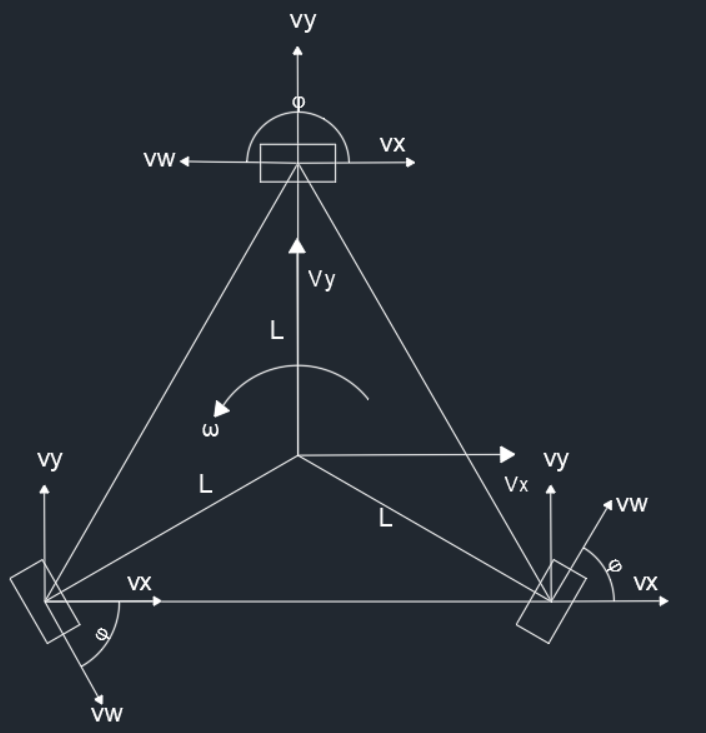
三舵轮底盘的控制与四舵轮底盘的控制相似，只是角速度的控制会不一致

直角坐标速度分析

如图，轮子直角坐标速度与机体的直角坐标速度一致，也就是

$v_{ixx}=V_x\\v_{ixy}=0\\v_{iyx}=0\\v_{iyy}=V_y\\$

角速度分析

机体转动的角速度需要映射为轮子转动的线速度，也就是

$v_{iw}=L_iw$

最终速度

将角速度映射到直角坐标上

$v_{ix}=v_{ixx}+v_{iyx}+v_{iw}\cos\varphi\\v_{iy}=v_{ixy}+v_{iyy}+v_{iw}\sin\varphi$

驱动轮的速度

$v_i=\sqrt{v_{ix}^2+v_{iy}^2}$

舵角解算

$\theta_i=\arctan\frac{v_{iy}}{v_{ix}}$

三全向轮底盘控制

三全向轮与四全向轮的解算也很相似，只需要把所有的速度映射到轮子转动的方向就可以了

直角坐标速度分析

如图，轮子直角坐标速度与机体的直角坐标速度一致，也就是

$v_{ixx}=V_x\\v_{ixy}=0\\v_{iyx}=0\\v_{iyy}=V_y\\$

角速度分析

机体转动的角速度需要映射为轮子转动的线速度，也就是

$v_{iw}=L_iw$

最终速度

$v_i=v_{iw}+(v_{ixx}+v_{iyx})\cos\varphi+(v_{ixy}+v_{iyy})\sin\varphi$