github仓库
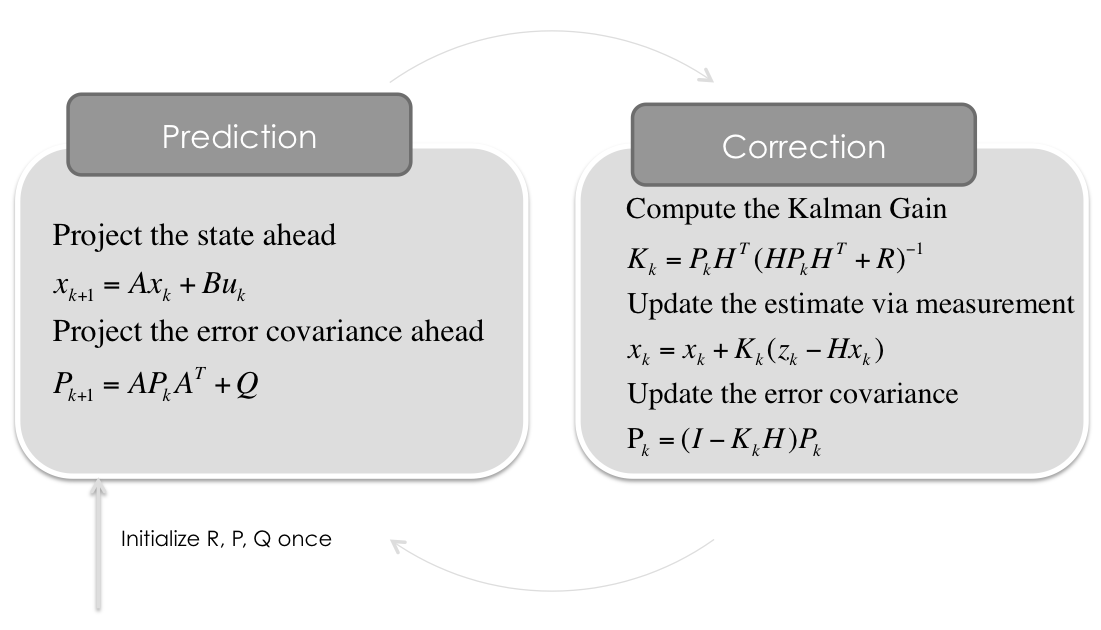
卡尔曼滤波 KF
公式
x ^ k ∣ k − 1 = F k x ^ k − 1 ∣ k − 1 P k ∣ k − 1 = F k P k − 1 ∣ k − 1 F k T + Q k K k = P k ∣ k − 1 H k T ( H k P k ∣ k − 1 H k T + R k ) − 1 x ^ k ∣ k = x ^ k ∣ k − 1 + K k ( z k − H k x ^ k ∣ k − 1 ) P k ∣ k = ( I − K k H k ) P k ∣ k − 1 \hat{x}_{k|k-1}=F_k\hat{x}_{k-1|k-1}\\P_{k|k-1}=F_kP_{k-1|k-1}F_k^T+Q_k\\K_k=P_{k|k-1}H_k^T(H_kP_{k|k-1}H_k^T+R_k)^{-1}\\\hat{x}_{k|k}=\hat{x}_{k|k-1}+K_k(z_k-H_k\hat{x}_{k|k-1})\\P_{k|k}=(I-K_kH_k)P_{k|k-1}
x ^ k ∣ k − 1 = F k x ^ k − 1 ∣ k − 1 P k ∣ k − 1 = F k P k − 1 ∣ k − 1 F k T + Q k K k = P k ∣ k − 1 H k T ( H k P k ∣ k − 1 H k T + R k ) − 1 x ^ k ∣ k = x ^ k ∣ k − 1 + K k ( z k − H k x ^ k ∣ k − 1 ) P k ∣ k = ( I − K k H k ) P k ∣ k − 1
基本假设
卡尔曼滤波模型假设k时刻的真实状态是从(k − 1)时刻的状态演化而来
状态估计方程
x k = F k x k − 1 + B k u k + w k x_k=F_kx_{k-1}+B_ku_k+w_k
x k = F k x k − 1 + B k u k + w k
其中
F k F_k F k B k B_k B k u k u_k u k w k − N ( 0 , Q k ) w_k-N(0,Q_k) w k − N ( 0 , Q k ) x k x_k x k
状态估计转移方程
z k = H k x k + v k z_k=H_kx_k+v_k
z k = H k x k + v k
表示 k 时刻真实 x k x_k x k
其中
H k H_k H k v k ∼ N ( 0 , R k ) v_k\sim N(0,R_k) v k ∼ N ( 0 , R k )
初始状态以及每一时刻的噪声 x 0 , w 1 , … , w k , v 1 , … v k x_0,w_1,…,w_k,v_1,…v_k x 0 , w 1 , … , w k , v 1 , … v k
小结
从以上出发,可以计算相应的协方差矩阵,这个也是公式推导的主要部分。
预测
x ^ k ∣ k − 1 = F k x ^ k − 1 ∣ k − 1 \hat{x}_{k|k-1}=F_k\hat{x}_{k-1|k-1}
x ^ k ∣ k − 1 = F k x ^ k − 1 ∣ k − 1
估计状态方程 ,表示预测下一步状态。
其中
x ^ k ∣ k − 1 \hat{x}_{k|k-1} x ^ k ∣ k − 1 x ^ k − 1 ∣ k − 1 \hat{x}_{k-1|k-1} x ^ k − 1 ∣ k − 1 F k F_k F k
P k ∣ k − 1 = F k P k − 1 ∣ k − 1 F k T + Q k P_{k|k-1}=F_kP_{k-1|k-1}F_k^T+Q_k
P k ∣ k − 1 = F k P k − 1 ∣ k − 1 F k T + Q k
预测二估计协方差方程 ,预测误差方差,计算先验概率
其中
P k − 1 ∣ k − 1 P_{k-1|k-1} P k − 1 ∣ k − 1 P k ∣ k − 1 P_{k|k-1} P k ∣ k − 1 Q k Q_k Q k Q k = c o v ( Z , Z ) Q_k=cov(Z, Z) Q k = c o v ( Z , Z )
更新 K k = P k ∣ k − 1 H k T ( H k P k ∣ k − 1 H k T + R k ) − 1 K_k=P_{k|k-1}H_k^T(H_kP_{k|k-1}H_k^T+R_k)^{-1}
K k = P k ∣ k − 1 H k T ( H k P k ∣ k − 1 H k T + R k ) − 1
卡尔曼增益方程
其中
K k K_k K k R k R_k R k
x ^ k ∣ k = x ^ k ∣ k − 1 + K k ( z k − H k x ^ k ∣ k − 1 ) \hat{x}_{k|k}=\hat{x}_{k|k-1}+K_k(z_k-H_k\hat{x}_{k|k-1})
x ^ k ∣ k = x ^ k ∣ k − 1 + K k ( z k − H k x ^ k ∣ k − 1 )
更新状态估计方程——最终滤波的效果
可以使用测量残差来简化表达公式,即
y ^ = z k − H k x ^ k ∣ k − 1 S k = c o v ( y ^ ) = H k P k ∣ k − 1 H k T + R k \hat{y}=z_k-H_k\hat{x}_{k|k-1}\\S_k=cov(\hat{y})=H_kP_{k|k-1}H_k^T+R_k
y ^ = z k − H k x ^ k ∣ k − 1 S k = c o v ( y ^ ) = H k P k ∣ k − 1 H k T + R k
即卡尔曼增益可以简化为
K k = P k ∣ k − 1 H k T S k − 1 K_k=P_{k|k-1}H_k^TS_k^{-1}
K k = P k ∣ k − 1 H k T S k − 1
状态估计更新可以简化为
x ^ k ∣ k = x ^ k ∣ k − 1 + K k y ^ \hat{x}_{k|k}=\hat{x}_{k|k-1}+K_k\hat{y}
x ^ k ∣ k = x ^ k ∣ k − 1 + K k y ^
其中 c o v ( x ) cov(x) c o v ( x ) M × N M \times N M × N ,则 c o v ( X ) cov(X) c o v ( X ) 大小 为 N × N N\times N N × N c o v ( X ) cov(X) c o v ( X ) ( i , j ) (i,j) ( i , j ) C ( X i , X j ) C(Xi,Xj) C ( X i , X j )
P k ∣ k = ( I − K k H k ) P k ∣ k − 1 P_{k|k}=(I-K_kH_k)P_{k|k-1}
P k ∣ k = ( I − K k H k ) P k ∣ k − 1
更新估计协方差——得到后验概率
公式推导
首先 Q k Q_k Q k R k R_k R k
Q k = c o v ( w k ) = E ( w k w k T ) R k = c o v ( v k ) = E ( v k v k T ) P k ∣ k − 1 = c o v ( x k − x ^ k ∣ k − 1 ) = E ( ( x k − x ^ k ∣ k − 1 ) ( x k − x ^ k ∣ k − 1 ) T ) P k ∣ k = c o v ( x k − x ^ k ∣ k ) = E ( ( x k − x ^ k ∣ k ) ( x k − x ^ k ∣ k ) T ) S k = c o v ( y ^ ) = c o v ( z k − H k x ^ k ∣ k − 1 ) Q_k=cov(w_k)=E(w_kw_k^T)\\R_k=cov(v_k)=E(v_kv^T_k)\\P_{k|k-1}=cov(x_k-\hat{x}_{k|k-1})=E((x_k-\hat{x}_{k|k-1})(x_k-\hat{x}_{k|k-1})^T)\\P_{k|k}=cov(x_k-\hat{x}_{k|k})=E((x_k-\hat{x}_{k|k})(x_k-\hat{x}_{k|k})^T)\\S_k=cov(\hat{y})=cov(z_k-H_k\hat{x}_{k|k-1})
Q k = c o v ( w k ) = E ( w k w k T ) R k = c o v ( v k ) = E ( v k v k T ) P k ∣ k − 1 = c o v ( x k − x ^ k ∣ k − 1 ) = E ( ( x k − x ^ k ∣ k − 1 ) ( x k − x ^ k ∣ k − 1 ) T ) P k ∣ k = c o v ( x k − x ^ k ∣ k ) = E ( ( x k − x ^ k ∣ k ) ( x k − x ^ k ∣ k ) T ) S k = c o v ( y ^ ) = c o v ( z k − H k x ^ k ∣ k − 1 )
从状态估计方程推导 P k ∣ k − 1 P_{k|k-1} P k ∣ k − 1
P k ∣ k = c o v ( x k − x ^ k ∣ k ) = c o v ( x k − x ^ k ∣ k − 1 − K k ( z k − H k x ^ k ∣ k − 1 ) ) = c o v ( x k − x ^ k ∣ k − 1 − K k ( H k x k + v k − H k x ^ k ∣ k − 1 ) ) = c o v ( ( I − K k H k ) ( x k − x ^ k ∣ k − 1 ) − K k v k ) = c o v ( ( I − K k H k ) ( x k − x ^ k ∣ k − 1 ) + c o v ( K k v k ) = ( I − K k H k ) c o v ( x k − x ^ k ∣ k − 1 ) ( I − K k H k ) T + K k c o v ( v k ) K k T = ( I − K k H k ) P k ∣ k − 1 ( I − K k H k ) T + K k R k K k T P_{k|k}=cov(x_k-\hat{x}_{k|k})\\=cov(x_k-\hat{x}_{k|k-1}-K_k(z_k-H_k\hat{x}_{k|k-1}))\\=cov(x_k-\hat{x}_{k|k-1}-K_k(H_kx_k+v_k-H_k\hat{x}_{k|k-1}))\\=cov((I-K_kH_k)(x_k-\hat{x}_{k|k-1})-K_kv_k)\\=cov((I-K_kH_k)(x_k-\hat{x}_{k|k-1})+cov(K_kv_k)\\=(I-K_kH_k)cov(x_k-\hat{x}_{k|k-1})(I-K_kH_k)^T+K_kcov(v_k)K_k^T\\=(I-K_kH_k)P_{k|k-1}(I-K_kH_k)^T+K_kR_kK_k^T
P k ∣ k = c o v ( x k − x ^ k ∣ k ) = c o v ( x k − x ^ k ∣ k − 1 − K k ( z k − H k x ^ k ∣ k − 1 ) ) = c o v ( x k − x ^ k ∣ k − 1 − K k ( H k x k + v k − H k x ^ k ∣ k − 1 ) ) = c o v ( ( I − K k H k ) ( x k − x ^ k ∣ k − 1 ) − K k v k ) = c o v ( ( I − K k H k ) ( x k − x ^ k ∣ k − 1 ) + c o v ( K k v k ) = ( I − K k H k ) c o v ( x k − x ^ k ∣ k − 1 ) ( I − K k H k ) T + K k c o v ( v k ) K k T = ( I − K k H k ) P k ∣ k − 1 ( I − K k H k ) T + K k R k K k T
这一公式对任何卡尔曼增益 K k K_k K k K k K_k K k
推导最优卡尔曼增益 K k K_k K k
可以根据上式推导最优卡尔曼增益,卡尔曼滤波器是最小均方误差估计器,所以设定代价函数 J J J P k ∣ k = c o v ( x k − x ^ k ∣ k ) P_{k|k}=cov(x_k-\hat{x}_{k|k}) P k ∣ k = c o v ( x k − x ^ k ∣ k ) P k ∣ k P_{k|k} P k ∣ k P k ∣ k P_{k|k} P k ∣ k
P k ∣ k = ( I − K k H k ) P k ∣ k − 1 ( I − K k H k ) T + K k R k K k T = P k ∣ k − 1 − K k H k P k ∣ k − 1 − P k ∣ k − 1 ( K k H k ) T + K k ( H k P k ∣ k − 1 H k T + R k ) K k T P_{k|k}=(I-K_kH_k)P_{k|k-1}(I-K_kH_k)^T+K_kR_kK_k^T\\=P_{k|k-1}-K_kH_kP_{k|k-1}-P_{k|k-1}(K_kH_k)^T+K_k(H_kP_{k|k-1}H_k^T+R_k)K_k^T
P k ∣ k = ( I − K k H k ) P k ∣ k − 1 ( I − K k H k ) T + K k R k K k T = P k ∣ k − 1 − K k H k P k ∣ k − 1 − P k ∣ k − 1 ( K k H k ) T + K k ( H k P k ∣ k − 1 H k T + R k ) K k T
求解该矩阵的迹
t r ( P k ∣ k ) = t r ( P k ∣ k − 1 − K k H k P k ∣ k − 1 − P k ∣ k − 1 ( K k H k ) T + K k ( H k P k ∣ k − 1 H k T + R k ) K k T ) = t r ( P k ∣ k − 1 ) − 2 t r ( K k H k P k ∣ k − 1 ) + t r ( K k ( H k P k ∣ k − 1 H k T + R k ) K k T ) tr(P_{k|k})=tr(P_{k|k-1}-K_kH_kP_{k|k-1}-P_{k|k-1}(K_kH_k)^T+K_k(H_kP_{k|k-1}H_k^T+R_k)K_k^T)\\=tr(P_{k|k-1})-2tr(K_kH_kP_{k|k-1})+tr(K_k(H_kP_{k|k-1}H_k^T+R_k)K_k^T)
t r ( P k ∣ k ) = t r ( P k ∣ k − 1 − K k H k P k ∣ k − 1 − P k ∣ k − 1 ( K k H k ) T + K k ( H k P k ∣ k − 1 H k T + R k ) K k T ) = t r ( P k ∣ k − 1 ) − 2 t r ( K k H k P k ∣ k − 1 ) + t r ( K k ( H k P k ∣ k − 1 H k T + R k ) K k T )
上式对 K k K_k K k
d t r ( P k ∣ k ) d K k = d [ t r ( P k ∣ k − 1 ) − 2 t r ( K k H k P k ∣ k − 1 ) + t r ( K k ( H k P k ∣ k − 1 H k T + R k ) K k T ) ] d K k = − 2 ( H k P k ∣ k − 1 ) T + 2 K k ( H k P k ∣ k − 1 H k T + R k ) \frac{d~tr(P_{k|k})}{d~K_k}=\frac{d[tr(P_{k|k-1})-2tr(K_kH_kP_{k|k-1})+tr(K_k(H_kP_{k|k-1}H_k^T+R_k)K_k^T)]}{d~K_k}\\=-2(H_kP_{k|k-1})^T+2K_k(H_kP_{k|k-1}H_k^T+R_k)
d K k d t r ( P k ∣ k ) = d K k d [ t r ( P k ∣ k − 1 ) − 2 t r ( K k H k P k ∣ k − 1 ) + t r ( K k ( H k P k ∣ k − 1 H k T + R k ) K k T ) ] = − 2 ( H k P k ∣ k − 1 ) T + 2 K k ( H k P k ∣ k − 1 H k T + R k )
当导数为 0 时取极值,即
− 2 ( H k P k ∣ k − 1 ) T + 2 K k ( H k P k ∣ k − 1 H k T + R k ) = 0 -2(H_kP_{k|k-1})^T+2K_k(H_kP_{k|k-1}H_k^T+R_k)=0
− 2 ( H k P k ∣ k − 1 ) T + 2 K k ( H k P k ∣ k − 1 H k T + R k ) = 0
得
K k = ( H k P k ∣ k − 1 ) T ( H k P k ∣ k − 1 H k T + R k ) − 1 K_k=(H_kP_{k|k-1})^T(H_kP_{k|k-1}H_k^T+R_k)^{-1}
K k = ( H k P k ∣ k − 1 ) T ( H k P k ∣ k − 1 H k T + R k ) − 1
从上述可知
S k = H k P k ∣ k − 1 H k T + R k S_k=H_kP_{k|k-1}H_k^T+R_k
S k = H k P k ∣ k − 1 H k T + R k
得
K k = P k ∣ k − 1 H k T S k − 1 K_k=P_{k|k-1}H_k^TS_k^{-1}
K k = P k ∣ k − 1 H k T S k − 1
对该矩阵的迹求二阶导
d t r 2 ( P k ∣ k ) d K k 2 = 2 ( H k P k ∣ k − 1 H k − 1 + R k ) T \frac{d~tr^2(P_{k|k})}{d~K_k^2}=2(H_kP_{k|k-1}H_k^{-1}+R_k)^T
d K k 2 d t r 2 ( P k ∣ k ) = 2 ( H k P k ∣ k − 1 H k − 1 + R k ) T
由于 R k R_k R k v k v_k v k
最优卡尔曼增益化简 P k ∣ k P_{k|k} P k ∣ k
从上式化简得到
K k S k = ( H k P k ∣ k − 1 ) T K k S k K k T = ( H k P k ∣ k − 1 ) T K k T = P k ∣ k − 1 ( K k H k ) T K_kS_k=(H_kP_{k|k-1})^T\\K_kS_kK_k^T=(H_kP_{k|k-1})^TK_k^T=P_{k|k-1}(K_kH_k)^T
K k S k = ( H k P k ∣ k − 1 ) T K k S k K k T = ( H k P k ∣ k − 1 ) T K k T = P k ∣ k − 1 ( K k H k ) T
带入其中得
P k ∣ k = P k ∣ k − 1 − K k H k P k ∣ k − 1 − P k ∣ k − 1 ( K k H k ) T + K k ( H k P k ∣ k − 1 H k T + R k ) K k T = P k ∣ k − 1 − K k H k P k ∣ k − 1 − P k ∣ k − 1 ( K k H k ) T + K k S k K k T = ( I − K k H k ) P k ∣ k − 1 P_{k|k}=P_{k|k-1}-K_kH_kP_{k|k-1}-P_{k|k-1}(K_kH_k)^T+K_k(H_kP_{k|k-1}H_k^T+R_k)K_k^T\\=P_{k|k-1}-K_kH_kP_{k|k-1}-P_{k|k-1}(K_kH_k)^T+K_kS_kK_k^T\\=(I-K_kH_k)P_{k|k-1}
P k ∣ k = P k ∣ k − 1 − K k H k P k ∣ k − 1 − P k ∣ k − 1 ( K k H k ) T + K k ( H k P k ∣ k − 1 H k T + R k ) K k T = P k ∣ k − 1 − K k H k P k ∣ k − 1 − P k ∣ k − 1 ( K k H k ) T + K k S k K k T = ( I − K k H k ) P k ∣ k − 1
该简化式 P k ∣ k = ( I − K k H k ) P k ∣ k − 1 P_{k|k}=(I-K_kH_k)P_{k|k-1} P k ∣ k = ( I − K k H k ) P k ∣ k − 1 P k ∣ k = ( I − K k H k ) P k ∣ k − 1 ( I − K k H k ) T + K k R k K k T P_{k|k}=(I-K_kH_k)P_{k|k-1}(I-K_kH_k)^T+K_kR_kK_k^T P k ∣ k = ( I − K k H k ) P k ∣ k − 1 ( I − K k H k ) T + K k R k K k T
自适应卡尔曼滤波 AKF
首先列出系统方程
X k = A X k − 1 + C u k + B w k Y k = C X k + v k X_k=AX_{k-1}+Cu_k+Bw_k\\Y_k=CX_k+v_k
X k = A X k − 1 + C u k + B w k Y k = C X k + v k
其中
X k 表示状态量 Y k 表示输出量 u k 表示输入量 w k , v k 为噪声 X_k \text{表示状态量}\\Y_k \text{表示输出量}\\u_k \text{表示输入量}\\w_k,v_k \text{为噪声}
X k 表示状态量 Y k 表示输出量 u k 表示输入量 w k , v k 为噪声
E [ w k ] = q k E [ w k w k T ] = Q k δ t p E [ v k ] = r k E [ v k v k T ] = R k δ t p E[w_k]=q_k\\E[w_kw_k^T]=Q_k\delta_{tp}\\E[v_k]=r_k\\E[v_kv_k^T]=R_k\delta_{tp}
E [ w k ] = q k E [ w k w k T ] = Q k δ t p E [ v k ] = r k E [ v k v k T ] = R k δ t p
其中 Q ( t ) , R ( t ) , q ( t ) , r ( t ) Q(t),R(t),q(t),r(t) Q ( t ) , R ( t ) , q ( t ) , r ( t )
具体过程
预测方程
X ^ k ∣ k − 1 = A X ^ k − 1 ∣ k − 1 + C u k − 1 + B q ‾ k − 1 \hat{X}_{k|k-1}=A\hat{X}_{k-1|k-1}+Cu_{k-1}+B\overline{q}_{k-1}
X ^ k ∣ k − 1 = A X ^ k − 1 ∣ k − 1 + C u k − 1 + B q k − 1
其中 q ‾ k − 1 \overline{q}_{k-1} q k − 1
预测均方差误差方程
P k ∣ k − 1 = A P k − 1 ∣ k − 1 A T + B Q ‾ k − 1 B T P_{k|k-1}=AP_{k-1|k-1}A^T+B\overline{Q}_{k-1}B^T
P k ∣ k − 1 = A P k − 1 ∣ k − 1 A T + B Q k − 1 B T
其中 Q ‾ k − 1 \overline{Q}_{k-1} Q k − 1
更新滤波增益方程
K k = P k ∣ k − 1 C T ( C P k ∣ k − 1 C T + R ‾ k − 1 ) − 1 K_k=P_{k|k-1}C^T(CP_{k|k-1}C^T+\overline{R}_{k-1})^{-1}
K k = P k ∣ k − 1 C T ( C P k ∣ k − 1 C T + R k − 1 ) − 1
其中 R ‾ k − 1 \overline{R}_{k-1} R k − 1
计算残差
ε k = Y k − C X ^ k ∣ k − 1 − r ‾ k − 1 \varepsilon_k=Y_k-C\hat{X}_{k|k-1}-\overline{r}_{k-1}
ε k = Y k − C X ^ k ∣ k − 1 − r k − 1
其中 r ‾ k − 1 \overline{r}_{k-1} r k − 1
状态估计
X ^ k ∣ k = X ^ k ∣ k − 1 + K k ε k \hat{X}_{k|k}=\hat{X}_{k|k-1}+K_k\varepsilon_k
X ^ k ∣ k = X ^ k ∣ k − 1 + K k ε k
和卡尔曼滤波器的对应公式是一样的
均方差误差方程
P k ∣ k = ( I − K k C ) P k ∣ k − 1 P_{k|k}=(I-K_kC)P_{k|k-1}
P k ∣ k = ( I − K k C ) P k ∣ k − 1
和卡尔曼滤波器的对应公式是一样的
更新 q k , Q k , r k , R k q_k, Q_k, r_k, R_k q k , Q k , r k , R k
计算加权系数
d ( t ) = 1 − b 1 − b t + 1 0 < b < 1 d(t)=\frac{1-b}{1-b^{t+1}}~~~0<b<1
d ( t ) = 1 − b t + 1 1 − b 0 < b < 1
随着时间的推移, d ( t ) → 1 − b d(t)→1-b d ( t ) → 1 − b
d ( t ) = 1 t d(t)=\frac{1}{t}
d ( t ) = t 1
随着时间推移, d ( t ) → 0 d(t)→0 d ( t ) → 0 d ( t ) = 0 d(t)=0 d ( t ) = 0
更新 q ‾ k , Q ‾ k , r ‾ k , R ‾ k \overline{q}_k, \overline{Q}_k,\overline{r}_k,\overline{R}_k q k , Q k , r k , R k
q ‾ k = ( 1 − d ( k − 1 ) ) q ‾ k − 1 + d ( k − 1 ) ( X ^ k ∣ k − A X ^ k − 1 ∣ k − 1 ) Q ‾ k = ( 1 − d ( k − 1 ) ) Q ‾ k − 1 + d ( k − 1 ) ( K k ε k ε k T K k T + P k ∣ k − A P k − 1 ∣ k − 1 A T ) r ‾ k = ( 1 − d ( k − 1 ) ) r ‾ k − 1 + d ( k − 1 ) ( Y k − C X ^ k ∣ k − 1 ) R ‾ k = ( 1 − d ( k − 1 ) ) R ‾ k − 1 − d ( k − 1 ) ( ε k ε k T − C P k ∣ k − 1 C T ) \overline{q}_k=(1-d(k-1))\overline{q}_{k-1}+d(k-1)(\hat{X}_{k|k}-A\hat{X}_{k-1|k-1})\\\overline{Q}_k=(1-d(k-1))\overline{Q}_{k-1}+d(k-1)(K_k\varepsilon_k\varepsilon_k^TK_k^T+P_{k|k}-AP_{k-1|k-1}A^T)\\\overline{r}_k=(1-d(k-1))\overline{r}_{k-1}+d(k-1)(Y_k-C\hat{X}_{k|k-1})\\\overline{R}_{k}=(1-d(k-1))\overline{R}_{k-1}-d(k-1)(\varepsilon_k\varepsilon_k^T-CP_{k|k-1}C^T)
q k = ( 1 − d ( k − 1 ) ) q k − 1 + d ( k − 1 ) ( X ^ k ∣ k − A X ^ k − 1 ∣ k − 1 ) Q k = ( 1 − d ( k − 1 ) ) Q k − 1 + d ( k − 1 ) ( K k ε k ε k T K k T + P k ∣ k − A P k − 1 ∣ k − 1 A T ) r k = ( 1 − d ( k − 1 ) ) r k − 1 + d ( k − 1 ) ( Y k − C X ^ k ∣ k − 1 ) R k = ( 1 − d ( k − 1 ) ) R k − 1 − d ( k − 1 ) ( ε k ε k T − C P k ∣ k − 1 C T )
扩展卡尔曼滤波 EKF
用来解决非线性问题,如极坐标系的雷达,观测到的式径向距离和角度,这是观测矩阵 H 就是非线性的函数。EKF 与 KF 最主要的区别就是转换模型和观测模型可以是非线性的,可以使用泰勒展开式替换为线性函数,两个协方差矩阵 P 和 H 要使用雅各比矩阵计算每个状态量的一阶偏导。因为主要是状态估计方程和状态估计转移方程的两个地方有些区别,所以 EKF 协方差矩阵的公式推导还是跟 KF 一样的
对于非线性系统方程
x k = f ( x k − 1 , u k ) + w k z k = h ( x k ) + v k x_k=f(x_{k-1},u_k)+w_k\\z_k=h(x_k)+v_k
x k = f ( x k − 1 , u k ) + w k z k = h ( x k ) + v k
预测
x ^ k ∣ k − 1 = f ( x ^ k − 1 ∣ k − 1 , u k ) P k ∣ k − 1 = J F P k − 1 ∣ k − 1 J F T + Q k \hat{x}_{k|k-1}=f(\hat{x}_{k-1|k-1},u_k)\\P_{k|k-1}=J_FP_{k-1|k-1}J_F^T+Q_k
x ^ k ∣ k − 1 = f ( x ^ k − 1 ∣ k − 1 , u k ) P k ∣ k − 1 = J F P k − 1 ∣ k − 1 J F T + Q k
使用 Jacobians 矩阵更新模型
过程模型(矩阵)和测量模型(矩阵)与 KF 有所区别,需要进行雅各比矩阵求导运算
J F = ∂ f ∂ x ∣ x ^ k − 1 ∣ k − 1 , u k J H = ∂ h ∂ x ∣ x ^ k ∣ k − 1 J_F=\frac{\partial f}{\partial x}|_{\hat{x}_{k-1|k-1}, u_k}\\J_H=\frac{\partial h}{\partial x}|_{\hat{x}_{k|k-1}}
J F = ∂ x ∂ f ∣ x ^ k − 1 ∣ k − 1 , u k J H = ∂ x ∂ h ∣ x ^ k ∣ k − 1
更新
y ^ k = z k − h ( x ^ k ∣ k − 1 ) S k = J H P k ∣ k − 1 J H T + R k K k = P k ∣ k − 1 J H T S k − 1 x ^ k ∣ k = x ^ k ∣ k − 1 + K k y ^ P k ∣ k = ( I − K k J H ) P k ∣ k − 1 \hat{y}_k=z_k-h(\hat{x}_{k|k-1})\\S_k=J_HP_{k|k-1}J_H^T+R_k\\K_k=P_{k|k-1}J_H^TS_k^{-1}\\\hat{x}_{k|k}=\hat{x}_{k|k-1}+K_k\hat{y}\\P_{k|k}=(I-K_kJ_H)P_{k|k-1}
y ^ k = z k − h ( x ^ k ∣ k − 1 ) S k = J H P k ∣ k − 1 J H T + R k K k = P k ∣ k − 1 J H T S k − 1 x ^ k ∣ k = x ^ k ∣ k − 1 + K k y ^ P k ∣ k = ( I − K k J H ) P k ∣ k − 1
恒定转弯率和速度模型(Constant Turn Rate and Velocity——CTRV)
状态量为
X = [ x y v θ ω ] X=\begin{bmatrix}x\\y\\v\\\theta\\\omega\end{bmatrix}
X = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ x y v θ ω ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
状态方程为
X k + 1 = X k + [ ∫ t k t k + 1 v ( t ) c o s ( θ ( t ) ) d t ∫ t k t k + 1 v ( t ) s i n ( θ ( t ) ) d t 0 ω Δ t 0 ] X_{k+1}=X_k+\begin{bmatrix}\int_{t_k}^{t_{k+1}}{v(t)cos(\theta(t))}dt\\\int_{t_k}^{t_{k+1}}{v(t)sin(\theta(t))}dt\\0\\\omega \Delta t\\0\end{bmatrix}
X k + 1 = X k + ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ∫ t k t k + 1 v ( t ) c o s ( θ ( t ) ) d t ∫ t k t k + 1 v ( t ) s i n ( θ ( t ) ) d t 0 ω Δ t 0 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
其中在某一时刻将速度近似于常量,同时角速度也近似于常量。
对上式进行简化
∫ t k t k + 1 v ( t ) c o s ( θ ( t ) ) d t = v k ∫ t k t k + 1 c o s ( θ k + ω ( t − t k ) ) d t = v k ω [ s i n ( ω Δ + θ ) − s i n ( θ ) ] ∫ t k t k + 1 v ( t ) s i n ( θ ( t ) ) d t = v k ∫ t k t k + 1 s i n ( θ k + ω ( t − t k ) ) d t = v k ω [ − c o s ( ω Δ + θ ) + c o s ( θ ) ] \int_{t_k}^{t_{k+1}}{v(t)cos(\theta(t))}dt=v_k\int_{t_k}^{t_{k+1}}{cos(\theta_k+\omega (t-t_k))}dt=\frac{v_k}{\omega}[sin(\omega \Delta + \theta)- sin(\theta)]\\\int_{t_k}^{t_{k+1}}{v(t)sin(\theta(t))}dt=v_k\int_{t_k}^{t_{k+1}}{sin(\theta_k+\omega (t-t_k))}dt=\frac{v_k}{\omega}[-cos(\omega \Delta + \theta)+ cos(\theta)]
∫ t k t k + 1 v ( t ) c o s ( θ ( t ) ) d t = v k ∫ t k t k + 1 c o s ( θ k + ω ( t − t k ) ) d t = ω v k [ s i n ( ω Δ + θ ) − s i n ( θ ) ] ∫ t k t k + 1 v ( t ) s i n ( θ ( t ) ) d t = v k ∫ t k t k + 1 s i n ( θ k + ω ( t − t k ) ) d t = ω v k [ − c o s ( ω Δ + θ ) + c o s ( θ ) ]
则,上式的最终状态方程为
X k + 1 = X k + [ v k ω [ s i n ( ω Δ + θ ) − s i n ( θ ) ] v k ω [ − c o s ( ω Δ + θ ) + c o s ( θ ) ] 0 ω Δ t 0 ] = [ x k + v k ω [ s i n ( ω Δ + θ ) − s i n ( θ ) ] y k + v k ω [ − c o s ( ω Δ + θ ) + c o s ( θ ) ] v k ω Δ t + θ ω ] X_{k+1}=X_k+\begin{bmatrix}\frac{v_k}{\omega}[sin(\omega \Delta + \theta)- sin(\theta)]\\\frac{v_k}{\omega}[-cos(\omega \Delta + \theta)+ cos(\theta)]\\0\\\omega \Delta t\\0\end{bmatrix}=\begin{bmatrix}x_k+\frac{v_k}{\omega}[sin(\omega \Delta + \theta)- sin(\theta)]\\y_k+\frac{v_k}{\omega}[-cos(\omega \Delta + \theta)+ cos(\theta)]\\v_k\\\omega \Delta t+\theta\\\omega\end{bmatrix}
X k + 1 = X k + ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ω v k [ s i n ( ω Δ + θ ) − s i n ( θ ) ] ω v k [ − c o s ( ω Δ + θ ) + c o s ( θ ) ] 0 ω Δ t 0 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ x k + ω v k [ s i n ( ω Δ + θ ) − s i n ( θ ) ] y k + ω v k [ − c o s ( ω Δ + θ ) + c o s ( θ ) ] v k ω Δ t + θ ω ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
对其中每个状态量求偏导得到雅各比矩阵 J F J_F J F
J F = [ 1 0 1 ω [ s i n ( ω Δ t + θ ) − s i n ( θ ) v k ω [ c o s ( ω Δ t + θ ) − c o s ( θ ) v k Δ t ω c o s ( ω Δ t + θ ) − v k ω 2 [ s i n ( ω Δ t + θ ) − s i n ( θ ) ] 0 1 1 ω [ − c o s ( ω Δ t + θ ) + c o s ( θ ) v k ω [ s i n ( ω Δ t + θ ) − s i n ( θ ) v k Δ t ω s i n ( ω Δ t + θ ) − v k ω 2 [ − c o s ( ω Δ t + θ ) + c o s ( θ ) ] 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 ] J_F=\begin{bmatrix}1&0&\frac{1}{\omega}[sin(\omega \Delta t+\theta)-sin(\theta)&\frac{v_k}{\omega}[cos(\omega \Delta t+\theta)-cos(\theta)&\frac{v_k\Delta t}{\omega}cos(\omega \Delta t+\theta)-\frac{v_k}{\omega^2}[sin(\omega \Delta t+\theta)-sin(\theta)]\\0&1&\frac{1}{\omega}[-cos(\omega \Delta t+\theta)+cos(\theta)&\frac{v_k}{\omega}[sin(\omega \Delta t+\theta)-sin(\theta)&\frac{v_k\Delta t}{\omega}sin(\omega \Delta t+\theta)-\frac{v_k}{\omega^2}[-cos(\omega \Delta t+\theta)+cos(\theta)]\\0&0&1&0&0\\0&0&0&1&0\\0&0&0&0&1\end{bmatrix}
J F = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 1 0 0 0 0 0 1 0 0 0 ω 1 [ s i n ( ω Δ t + θ ) − s i n ( θ ) ω 1 [ − c o s ( ω Δ t + θ ) + c o s ( θ ) 1 0 0 ω v k [ c o s ( ω Δ t + θ ) − c o s ( θ ) ω v k [ s i n ( ω Δ t + θ ) − s i n ( θ ) 0 1 0 ω v k Δ t c o s ( ω Δ t + θ ) − ω 2 v k [ s i n ( ω Δ t + θ ) − s i n ( θ ) ] ω v k Δ t s i n ( ω Δ t + θ ) − ω 2 v k [ − c o s ( ω Δ t + θ ) + c o s ( θ ) ] 0 0 1 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
对于观测矩阵,如果是线性的,不用做计算。如果是非线性的,同样可以使用求偏导数的方式计算出雅各比矩阵 J H J_H J H
假设传感器是毫米波雷达观,且观测量是
z k = [ ρ k θ k ρ ˙ k ] = [ x k 2 + y k 2 a r c t a n ( y k x k ) v x x k + v y y k x k 2 + y k 2 ] = [ x k 2 + y k 2 a r c t a n ( y k x k ) v x x k c o s ( θ ) + v y y k s i n ( θ ) x k 2 + y k 2 ] z_k=\begin{bmatrix}\rho_k\\\theta_k\\\dot{\rho}_k\end{bmatrix}=\begin{bmatrix}\sqrt{x_k^2+y_k^2}\\arctan(\frac{y_k}{x_k})\\\frac{v_xx_k+v_yy_k}{\sqrt{x_k^2+y_k^2}}\end{bmatrix}=\begin{bmatrix}\sqrt{x_k^2+y_k^2}\\arctan(\frac{y_k}{x_k})\\\frac{v_xx_kcos(\theta)+v_yy_ksin(\theta)}{\sqrt{x_k^2+y_k^2}}\end{bmatrix}
z k = ⎣ ⎢ ⎡ ρ k θ k ρ ˙ k ⎦ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎡ x k 2 + y k 2 a r c t a n ( x k y k ) x k 2 + y k 2 v x x k + v y y k ⎦ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎡ x k 2 + y k 2 a r c t a n ( x k y k ) x k 2 + y k 2 v x x k c o s ( θ ) + v y y k s i n ( θ ) ⎦ ⎥ ⎥ ⎤
上式对状态方程每个状态量求偏导,得到雅各比矩阵,即观测矩阵 J H J_H J H
J H = [ x x 2 + y 2 y x 2 + y 2 0 0 0 − y x 2 + y 2 x x 2 + y 2 0 0 0 y ( v c o s ( θ ) y − v s i n ( θ ) x ) ( x 2 + y 2 ) 3 2 x ( v s i n ( θ ) x − v c o s ( θ ) y ) ( x 2 + y 2 ) 3 2 x c o s ( θ ) + y s i n ( θ ) x 2 + y 2 v c o s ( θ ) y − v s i n ( θ ) x x 2 + y 2 0 ] J_H=\begin{bmatrix}\frac{x}{\sqrt{x^2+y^2}}&\frac{y}{\sqrt{x^2+y^2}}&0&0&0\\-\frac{y}{x^2+y^2}&\frac{x}{x^2+y^2}&0&0&0\\\frac{y(vcos(\theta)y-vsin(\theta)x)}{(x^2+y^2)^{\frac{3}{2}}}&\frac{x(vsin(\theta)x-vcos(\theta)y)}{(x^2+y^2)^{\frac{3}{2}}}&\frac{xcos(\theta)+ysin(\theta)}{\sqrt{x^2+y^2}}&\frac{vcos(\theta)y-vsin(\theta)x}{\sqrt{x^2+y^2}}&0\end{bmatrix}
J H = ⎣ ⎢ ⎢ ⎢ ⎡ x 2 + y 2 x − x 2 + y 2 y ( x 2 + y 2 ) 2 3 y ( v c o s ( θ ) y − v s i n ( θ ) x ) x 2 + y 2 y x 2 + y 2 x ( x 2 + y 2 ) 2 3 x ( v s i n ( θ ) x − v c o s ( θ ) y ) 0 0 x 2 + y 2 x c o s ( θ ) + y s i n ( θ ) 0 0 x 2 + y 2 v c o s ( θ ) y − v s i n ( θ ) x 0 0 0 ⎦ ⎥ ⎥ ⎥ ⎤
Q矩阵计算
对于 CTRV,假设直线加速度 a a a_a a a a ω a_{\omega} a ω a a a_a a a a ω a_\omega a ω
a a ∼ N ( 0 , σ a 2 ) a ω ∼ N ( 0 , σ ω 2 ) a_a\sim N(0,\sigma_a^2)\\a_\omega\sim N(0,\sigma_\omega^2)
a a ∼ N ( 0 , σ a 2 ) a ω ∼ N ( 0 , σ ω 2 )
则这两个加速度对状态量的预测噪声为
w = [ Δ t 2 c o s ( θ ) a a 2 Δ t 2 s i n ( θ ) a a 2 Δ t a a Δ t 2 a ω 2 Δ t a ω ] = [ Δ t 2 c o s ( θ ) 2 0 Δ t 2 s i n ( θ ) 2 0 Δ t 0 0 Δ t 2 2 0 Δ t ] [ a a a ω ] = G u w=\begin{bmatrix}\frac{\Delta t^2cos(\theta)a_a}{2}\\\frac{\Delta t^2sin(\theta)a_a}{2}\\\Delta t a_a\\\frac{\Delta t^2a_\omega}{2}\\\Delta t a_\omega\end{bmatrix}=\begin{bmatrix}\frac{\Delta t^2cos(\theta)}{2}&0\\\frac{\Delta t^2sin(\theta)}{2}&0\\\Delta t&0\\0&\frac{\Delta t^2}{2}\\0&\Delta t \end{bmatrix}\begin{bmatrix}a_a\\a_\omega \end{bmatrix}=Gu
w = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 2 Δ t 2 c o s ( θ ) a a 2 Δ t 2 s i n ( θ ) a a Δ t a a 2 Δ t 2 a ω Δ t a ω ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 2 Δ t 2 c o s ( θ ) 2 Δ t 2 s i n ( θ ) Δ t 0 0 0 0 0 2 Δ t 2 Δ t ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ [ a a a ω ] = G u
则
Q = c o v ( w ) = E ( w w T ) = G E ( u u T ) G T = G [ σ a 2 0 0 σ ω 2 ] G T Q=cov(w)=E(ww^T)=GE(uu^T)G^T=G\begin{bmatrix}\sigma_a^2&0\\0&\sigma_\omega^2 \end{bmatrix}G^T
Q = c o v ( w ) = E ( w w T ) = G E ( u u T ) G T = G [ σ a 2 0 0 σ ω 2 ] G T
带入之后得
Q = [ T 4 σ a 2 c o s 2 ( θ ) 4 T 4 σ a 2 c o s ( θ ) s i n ( θ ) 4 T 3 σ a 2 c o s ( θ ) 2 0 0 T 4 σ a 2 s i n ( θ ) c o s ( θ ) 4 T 4 σ a 2 s i n 2 ( θ ) 4 T 3 σ a 2 s i n ( θ ) 2 0 0 T 3 σ a 2 c o s ( θ ) 2 T 3 σ a 2 s i n ( θ ) 2 T 2 σ a 2 0 0 0 0 0 T 4 σ a 2 4 T 3 σ ω 2 2 0 0 0 T 3 σ ω 2 2 T 2 σ ω 2 ] Q=\begin{bmatrix}\frac{T^4\sigma_a^2cos^2(\theta)}{4}&\frac{T^4\sigma_a^2cos(\theta)sin(\theta)}{4}&\frac{T^3\sigma_a^2cos(\theta)}{2}&0&0\\\frac{T^4\sigma_a^2sin(\theta)cos(\theta)}{4}&\frac{T^4\sigma_a^2sin^2(\theta)}{4}&\frac{T^3\sigma_a^2sin(\theta)}{2}&0&0\\\frac{T^3\sigma_a^2cos(\theta)}{2}&\frac{T^3\sigma_a^2sin(\theta)}{2}&T^2\sigma_a^2&0&0\\0&0&0&\frac{T^4\sigma_a^2}{4}&\frac{T^3\sigma_\omega^2}{2}\\0&0&0&\frac{T^3\sigma_\omega^2}{2}&T^2\sigma_\omega^2\end{bmatrix}
Q = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 4 T 4 σ a 2 c o s 2 ( θ ) 4 T 4 σ a 2 s i n ( θ ) c o s ( θ ) 2 T 3 σ a 2 c o s ( θ ) 0 0 4 T 4 σ a 2 c o s ( θ ) s i n ( θ ) 4 T 4 σ a 2 s i n 2 ( θ ) 2 T 3 σ a 2 s i n ( θ ) 0 0 2 T 3 σ a 2 c o s ( θ ) 2 T 3 σ a 2 s i n ( θ ) T 2 σ a 2 0 0 0 0 0 4 T 4 σ a 2 2 T 3 σ ω 2 0 0 0 2 T 3 σ ω 2 T 2 σ ω 2 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
常用的CV模型 的状态量为
X = [ x y v x v y ] X=\begin{bmatrix}x\\y\\v_x\\v_y\end{bmatrix}
X = ⎣ ⎢ ⎢ ⎢ ⎡ x y v x v y ⎦ ⎥ ⎥ ⎥ ⎤
其状态方程为
X k + 1 = X k + [ v x Δ t v y Δ t 0 0 ] = [ x k + v x Δ t y k + v y Δ t v x v y ] X_{k+1}=X_k+\begin{bmatrix}v_x\Delta t\\v_y\Delta t\\0\\0\end{bmatrix}=\begin{bmatrix}x_k+v_x\Delta t\\y_k+v_y\Delta t\\v_x\\v_y\end{bmatrix}
X k + 1 = X k + ⎣ ⎢ ⎢ ⎢ ⎡ v x Δ t v y Δ t 0 0 ⎦ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎡ x k + v x Δ t y k + v y Δ t v x v y ⎦ ⎥ ⎥ ⎥ ⎤
该式子对状态量中的每个参数求偏导,得到 J F J_F J F
J F = [ 1 0 Δ t 0 0 1 0 Δ t 0 0 1 0 0 0 0 1 ] J_F=\begin{bmatrix}1&0&\Delta t&0\\0&1&0&\Delta t\\0&0&1&0\\0&0&0&1\end{bmatrix}
J F = ⎣ ⎢ ⎢ ⎢ ⎡ 1 0 0 0 0 1 0 0 Δ t 0 1 0 0 Δ t 0 1 ⎦ ⎥ ⎥ ⎥ ⎤
如果假设观测量为
z k = [ ρ k θ k ρ ˙ k ] = [ x k 2 + y k 2 a r c t a n ( y k x k ) v x x k + v y y k x k 2 + y k 2 ] z_k=\begin{bmatrix}\rho_k\\\theta_k\\\dot{\rho}_k\end{bmatrix}=\begin{bmatrix}\sqrt{x_k^2+y_k^2}\\arctan(\frac{y_k}{x_k})\\\frac{v_xx_k+v_yy_k}{\sqrt{x_k^2+y_k^2}}\end{bmatrix}
z k = ⎣ ⎢ ⎡ ρ k θ k ρ ˙ k ⎦ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎡ x k 2 + y k 2 a r c t a n ( x k y k ) x k 2 + y k 2 v x x k + v y y k ⎦ ⎥ ⎥ ⎤
该式子对系统状态量中每个参数求偏导,得到 J H J_H J H
J H = [ x k x k 2 + y k 2 y k x k 2 + y k 2 0 0 − y k x k 2 + y K 2 x k x k 2 + y k 2 0 0 y k ( v x y k − v y x k ) ( x k 2 + y k 2 ) 3 2 x k ( v y x k − v x y k ) ( x k 2 + y k 2 ) 3 2 x k x k 2 + y k 2 y k x k 2 + y k 2 ] J_H=\begin{bmatrix}\frac{x_k}{\sqrt{x_k^2+y_k^2}}&\frac{y_k}{\sqrt{x_k^2+y_k^2}}&0&0\\-\frac{y_k}{x_k^2+y_K^2}&\frac{x_k}{x_k^2+y_k^2}&0&0\\\frac{y_k(v_xy_k-v_yx_k)}{(x_k^2+y_k^2)^{\frac{3}{2}}}&\frac{x_k(v_yx_k-v_xy_k)}{(x_k^2+y_k^2)^{\frac{3}{2}}}&\frac{x_k}{\sqrt{x_k^2+y_k^2}}&\frac{y_k}{\sqrt{x_k^2+y_k^2}}\end{bmatrix}
J H = ⎣ ⎢ ⎢ ⎢ ⎡ x k 2 + y k 2 x k − x k 2 + y K 2 y k ( x k 2 + y k 2 ) 2 3 y k ( v x y k − v y x k ) x k 2 + y k 2 y k x k 2 + y k 2 x k ( x k 2 + y k 2 ) 2 3 x k ( v y x k − v x y k ) 0 0 x k 2 + y k 2 x k 0 0 x k 2 + y k 2 y k ⎦ ⎥ ⎥ ⎥ ⎤
Q矩阵计算
对于 CV,假设直线加速度 a x a_x a x a y a_{y} a y a x a_x a x a y a_y a y
a x ∼ N ( 0 , σ a 2 ) a y ∼ N ( 0 , σ ω 2 ) a_x\sim N(0,\sigma_a^2)\\a_y\sim N(0,\sigma_\omega^2)
a x ∼ N ( 0 , σ a 2 ) a y ∼ N ( 0 , σ ω 2 )
w = [ Δ t 2 a x 2 Δ t 2 a y 2 Δ t a x Δ t a y ] = [ Δ t 2 2 0 0 Δ t 2 2 Δ t 0 0 Δ t ] [ a x a y ] = G u w=\begin{bmatrix}\frac{\Delta t^2a_x}{2}\\\frac{\Delta t^2a_y}{2}\\\Delta t a_x\\\Delta t a_y\end{bmatrix}=\begin{bmatrix}\frac{\Delta t^2}{2}&0\\0&\frac{\Delta t^2}{2}\\\Delta t&0\\0&\Delta t \end{bmatrix}\begin{bmatrix}a_x\\a_y\end{bmatrix}=Gu
w = ⎣ ⎢ ⎢ ⎢ ⎡ 2 Δ t 2 a x 2 Δ t 2 a y Δ t a x Δ t a y ⎦ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎡ 2 Δ t 2 0 Δ t 0 0 2 Δ t 2 0 Δ t ⎦ ⎥ ⎥ ⎥ ⎤ [ a x a y ] = G u
则
Q = c o v ( w ) = E ( w w T ) = G E ( u u T ) G T = G [ σ x 2 0 0 σ y 2 ] G T Q=cov(w)=E(ww^T)=GE(uu^T)G^T=G\begin{bmatrix}\sigma_x^2&0\\0&\sigma_y^2 \end{bmatrix}G^T
Q = c o v ( w ) = E ( w w T ) = G E ( u u T ) G T = G [ σ x 2 0 0 σ y 2 ] G T
Q = [ T 4 σ x 2 4 0 T 3 σ x 2 2 0 0 T 4 σ y 2 4 0 T 3 σ y 2 2 T 3 σ x 2 2 0 T 2 σ x 2 0 0 T 3 σ y 2 2 0 T 2 σ y 2 ] Q=\begin{bmatrix}\frac{T^4\sigma_x^2}{4}&0&\frac{T^3\sigma_x^2}{2}&0\\0&\frac{T^4\sigma_y^2}{4}&0&\frac{T^3\sigma_y^2}{2}\\\frac{T^3\sigma_x^2}{2}&0&T^2\sigma_x^2&0\\0&\frac{T^3\sigma_y^2}{2}&0&T^2\sigma_y^2\end{bmatrix}
Q = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 4 T 4 σ x 2 0 2 T 3 σ x 2 0 0 4 T 4 σ y 2 0 2 T 3 σ y 2 2 T 3 σ x 2 0 T 2 σ x 2 0 0 2 T 3 σ y 2 0 T 2 σ y 2 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
恒定转弯率和加速度模型(Constant Turn Rate and Velocity——CTRA)——过于复杂
其中的系统状态量为
X = [ x y θ v ω a ] X=\begin{bmatrix}x\\y\\\theta\\v\\\omega\\a\end{bmatrix}
X = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ x y θ v ω a ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
系统状态方程为
X k + 1 = X k + [ ∫ t k t k + 1 v ( t ) c o s ( θ ( t ) ) d t ∫ t k t k + 1 v ( t ) s i n ( θ ( t ) ) d t ω Δ t a Δ t 0 0 ] X_{k+1}=X_k+\begin{bmatrix}\int_{t_k}^{t_{k+1}}{v(t)cos(\theta(t))}dt\\\int_{t_k}^{t_{k+1}}{v(t)sin(\theta(t))}dt\\\omega \Delta t\\a\Delta t\\0\\0\end{bmatrix}
X k + 1 = X k + ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ∫ t k t k + 1 v ( t ) c o s ( θ ( t ) ) d t ∫ t k t k + 1 v ( t ) s i n ( θ ( t ) ) d t ω Δ t a Δ t 0 0 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
其中 a a a ω \omega ω Δ t = t k + 1 − t k \Delta t=t_{k+1}-t_k Δ t = t k + 1 − t k
∫ t k t k + 1 v ( t ) c o s ( θ ( t ) ) d t = ∫ t k t k + 1 ( v k + a ( t − t k ) ) c o s ( θ k + ω ( t − t k ) ) d t = 1 ω 2 [ ( v k ω + a ω Δ t ) s i n ( θ k + ω Δ t ) + a c o s ( θ k + ω Δ t ) − v k ω s i n ( θ k ) − a c o s ( θ k ) ] ∫ t k t k + 1 v ( t ) s i n ( θ ( t ) ) d t = ∫ t k t k + 1 ( v k + a ( t − t k ) ) s i n ( θ k + ω ( t − t k ) ) d t = 1 ω 2 [ − ( v k ω + a ω Δ t ) c o s ( θ k + ω Δ t ) − a s i n ( θ k + ω Δ t ) + v k ω c o s ( θ k ) + a s i n ( θ k ) ] \int_{t_k}^{t_{k+1}}{v(t)cos(\theta(t))}dt=\int_{t_k}^{t_{k+1}}{(v_k+a(t-t_k))cos(\theta_k+\omega(t-t_k))}dt=\frac{1}{\omega^2}[(v_k\omega+a\omega\Delta t)sin(\theta_k+\omega \Delta t)+acos(\theta_k+\omega\Delta t)-v_k\omega sin(\theta_k)-acos(\theta_k)]\\\int_{t_k}^{t_{k+1}}{v(t)sin(\theta(t))}dt=\int_{t_k}^{t_{k+1}}{(v_k+a(t-t_k))sin(\theta_k+\omega(t-t_k))}dt=\frac{1}{\omega^2}[-(v_k\omega+a\omega\Delta t)cos(\theta_k+\omega \Delta t)-asin(\theta_k+\omega\Delta t)+v_k\omega cos(\theta_k)+asin(\theta_k)]
∫ t k t k + 1 v ( t ) c o s ( θ ( t ) ) d t = ∫ t k t k + 1 ( v k + a ( t − t k ) ) c o s ( θ k + ω ( t − t k ) ) d t = ω 2 1 [ ( v k ω + a ω Δ t ) s i n ( θ k + ω Δ t ) + a c o s ( θ k + ω Δ t ) − v k ω s i n ( θ k ) − a c o s ( θ k ) ] ∫ t k t k + 1 v ( t ) s i n ( θ ( t ) ) d t = ∫ t k t k + 1 ( v k + a ( t − t k ) ) s i n ( θ k + ω ( t − t k ) ) d t = ω 2 1 [ − ( v k ω + a ω Δ t ) c o s ( θ k + ω Δ t ) − a s i n ( θ k + ω Δ t ) + v k ω c o s ( θ k ) + a s i n ( θ k ) ]
所以上式最终可以表示为
X k + 1 = [ x k + 1 ω 2 [ ( v k ω + a ω Δ t ) s i n ( θ k + ω Δ t ) + a c o s ( θ k + ω Δ t ) − v k ω s i n ( θ k ) − a c o s ( θ k ) ] y + 1 ω 2 [ − ( v k ω + a ω Δ t ) c o s ( θ k + ω Δ t ) − a s i n ( θ k + ω Δ t ) + v k ω c o s ( θ k ) + a s i n ( θ k ) ] θ k + ω Δ t v k + a Δ t ω a ] X_{k+1}=\begin{bmatrix}x_k+\frac{1}{\omega^2}[(v_k\omega+a\omega\Delta t)sin(\theta_k+\omega \Delta t)+acos(\theta_k+\omega\Delta t)-v_k\omega sin(\theta_k)-acos(\theta_k)]\\y+\frac{1}{\omega^2}[-(v_k\omega+a\omega\Delta t)cos(\theta_k+\omega \Delta t)-asin(\theta_k+\omega\Delta t)+v_k\omega cos(\theta_k)+asin(\theta_k)]\\\theta_k+\omega \Delta t\\v_k+a\Delta t\\\omega\\a\end{bmatrix}
X k + 1 = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ x k + ω 2 1 [ ( v k ω + a ω Δ t ) s i n ( θ k + ω Δ t ) + a c o s ( θ k + ω Δ t ) − v k ω s i n ( θ k ) − a c o s ( θ k ) ] y + ω 2 1 [ − ( v k ω + a ω Δ t ) c o s ( θ k + ω Δ t ) − a s i n ( θ k + ω Δ t ) + v k ω c o s ( θ k ) + a s i n ( θ k ) ] θ k + ω Δ t v k + a Δ t ω a ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
对状态方程的每个状态量求偏导,得到雅各比矩阵 J F J_F J F
J F = [ 1 0 1 ω 2 [ ( v ω + a ω T ) c o s ( θ + ω T ) − a s i n ( θ + ω T ) − v ω c o s ( θ ) + a s i n ( θ ) ] 1 ω 2 [ ω s i n ( θ + ω T ) − ω s i n ( θ ) ] − T a s i n ( T ω + θ ) + T ( T ω a + ω v ) c o s ( T ω + θ ) − v s i n ( θ ) + ( T a + v ) s i n ( T ω + θ ) ω 2 − 2 ( − ω v s i n ( θ ) − a c o s ( θ ) + a c o s ( T ω + a ) + ( T ω a + ω v ) s i n ( T ω + θ ) ω 3 T ω s i n ( T ω + θ ) − c o s ( θ ) + c o s ( T ω + θ ) ω 2 0 1 1 ω 2 [ ( v ω + a ω T ) s i n ( θ + ω T ) + a c o s ( θ + ω T ) + v ω s i n ( θ ) − a c o s ( θ ) ] 1 ω 2 [ − ω c o s ( θ + ω T ) + ω c o s ( θ ) ] T a c o s ( T ω + θ ) + T ( T ω a + ω v ) s i n ( T ω + θ ) + v c o s ( θ ) − ( T a + v ) c o s ( T ω + θ ) ω 2 − 2 ( ω v c o s ( θ ) − a s i n ( θ ) + a s i n ( T ω + a ) − ( T ω a + ω v ) c o s ( T ω + θ ) ω 3 − T ω c o s ( T ω + θ ) − s i n ( θ ) + s i n ( T ω + θ ) ω 2 0 0 1 0 T 0 0 0 0 1 0 T 0 0 0 0 1 0 0 0 0 0 0 1 ] J_F=\begin{bmatrix}1&0&\frac{1}{\omega^2}[(v\omega+a\omega T)cos(\theta+\omega T)-asin(\theta+\omega T)-v\omega cos(\theta)+asin(\theta)]&\frac{1}{\omega^2}[\omega sin(\theta+\omega T)-\omega sin(\theta)]&\frac{-Tasin(T\omega+\theta)+T(T\omega a+\omega v)cos(T\omega +\theta)-vsin(\theta)+(Ta+v)sin(T\omega+\theta)}{\omega^2}-\frac{2(-\omega vsin(\theta)-acos(\theta)+acos(T\omega+a)+(T\omega a+\omega v)sin(T\omega +\theta)}{\omega^3}&\frac{T\omega sin(T\omega +\theta)-cos(\theta)+cos(T\omega +\theta)}{\omega^2}\\0&1&\frac{1}{\omega^2}[(v\omega+a\omega T)sin(\theta+\omega T)+acos(\theta+\omega T)+v\omega sin(\theta)-acos(\theta)]&\frac{1}{\omega^2}[-\omega cos(\theta+\omega T)+\omega cos(\theta)]&\frac{Tacos(T\omega+\theta)+T(T\omega a+\omega v)sin(T\omega +\theta)+vcos(\theta)-(Ta+v)cos(T\omega+\theta)}{\omega^2}-\frac{2(\omega vcos(\theta)-asin(\theta)+asin(T\omega+a)-(T\omega a+\omega v)cos(T\omega +\theta)}{\omega^3}&\frac{-T\omega cos(T\omega +\theta)-sin(\theta)+sin(T\omega +\theta)}{\omega^2}\\0&0&1&0&T&0\\0&0&0&1&0&T\\0&0&0&0&1&0\\0&0&0&0&0&1\end{bmatrix}
J F = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 1 0 0 0 0 0 0 1 0 0 0 0 ω 2 1 [ ( v ω + a ω T ) c o s ( θ + ω T ) − a s i n ( θ + ω T ) − v ω c o s ( θ ) + a s i n ( θ ) ] ω 2 1 [ ( v ω + a ω T ) s i n ( θ + ω T ) + a c o s ( θ + ω T ) + v ω s i n ( θ ) − a c o s ( θ ) ] 1 0 0 0 ω 2 1 [ ω s i n ( θ + ω T ) − ω s i n ( θ ) ] ω 2 1 [ − ω c o s ( θ + ω T ) + ω c o s ( θ ) ] 0 1 0 0 ω 2 − T a s i n ( T ω + θ ) + T ( T ω a + ω v ) c o s ( T ω + θ ) − v s i n ( θ ) + ( T a + v ) s i n ( T ω + θ ) − ω 3 2 ( − ω v s i n ( θ ) − a c o s ( θ ) + a c o s ( T ω + a ) + ( T ω a + ω v ) s i n ( T ω + θ ) ω 2 T a c o s ( T ω + θ ) + T ( T ω a + ω v ) s i n ( T ω + θ ) + v c o s ( θ ) − ( T a + v ) c o s ( T ω + θ ) − ω 3 2 ( ω v c o s ( θ ) − a s i n ( θ ) + a s i n ( T ω + a ) − ( T ω a + ω v ) c o s ( T ω + θ ) T 0 1 0 ω 2 T ω s i n ( T ω + θ ) − c o s ( θ ) + c o s ( T ω + θ ) ω 2 − T ω c o s ( T ω + θ ) − s i n ( θ ) + s i n ( T ω + θ ) 0 T 0 1 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
无迹卡尔曼滤波 UKF
卡尔曼滤波(Kalman filtering)是一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响,所以最优估计也可看作是滤波过程。
无迹卡尔曼滤波(Unscented Kalman Filter,UKF),是无损变换(Unscented Transform,UT变换)与标准卡尔曼滤波体系的结合,通过无损变换变换使非线性系统方程适用于线性假设下的标准卡尔曼体系,相当于是 KF 基础上加入了 UT 变换
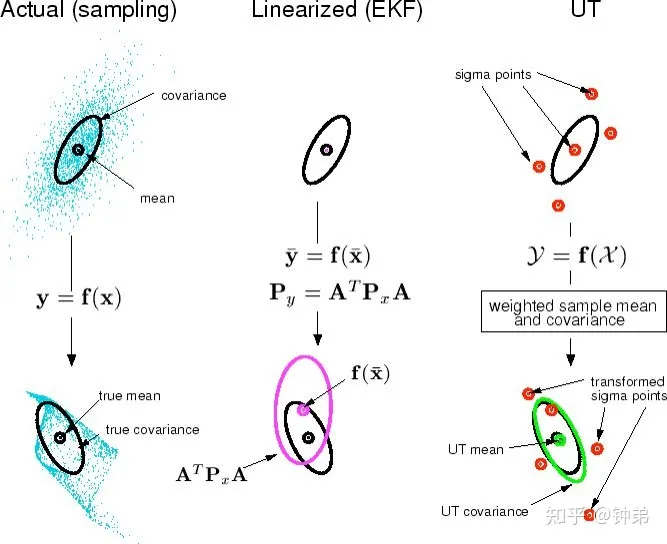
对于非线性问题的处理,过程模型F和测量模型H是非线性的,EKF是求一阶全导数得到线性模型,来近似非线性模型;而UKF是直接寻找一个与真实分布近似的高斯分布,没有用线性表征。
使用背景
对于某个系统,你拥有准确的数学模型(状态方程和观测方程),也就是说,给出这个系统的输入,你必然能算出这个系统的输出;但是,在现实生活中往往拿到的第一手测试数据并不是你想要的最直观的数据(而且数据还有噪声),这时候使用UKF可以依靠相对准确的数值模型和结合测试数据来得到你想要的信息
数值模型的参数相对不准确,但实测数据可信度更好,这时候使用UKF可以依靠相对准确的实测数据和结合数值模型来还原较真实的参数
核心思想
该算法的核心思想是:采用UT变换,利用一组Sigma采样点来描述随机变量的高斯分布,然后通过非线性函数的传递,再利用加权统计线性回归技术来近似非x线性函数的后验均值和方差。相比于EKF,UKF的估计精度能够达到泰勒级数展开的二阶精度
UKF的原理与实现流程
UT变换
例如函数 y = f ( x ) y=f(x) y = f ( x ) x ‾ \overline{x} x P x P_x P x { x i } , i = 0 , 1 , … , L \{x_i\},i=0,1,…,L { x i } , i = 0 , 1 , … , L ω m ( i ) \omega_m^{(i)} ω m ( i ) ω c ( i ) \omega_c^{(i)} ω c ( i ) { x i } , i = 0 , 1 , … , L \{x_i\},i=0,1,…,L { x i } , i = 0 , 1 , … , L y i = f ( x i ) y_i=f(x_i) y i = f ( x i ) y i y_i y i
y ‾ = ∑ i = 0 L ω m ( i ) y i P y y = ∑ i = 0 L ω c ( i ) ( y i − y ‾ ) ( y i − y ‾ ) T P x y = ∑ i = 0 L ω c ( i ) ( x i − x ‾ ) ( y i − y ‾ ) T \overline{y}=\sum_{i=0}^{L}{\omega_m^{(i)}y_i}\\P_{yy}=\sum_{i=0}^{L}{\omega_c^{(i)}(y_i-\overline{y})(y_i-\overline{y})^T}\\P_{xy}=\sum_{i=0}^{L}{\omega_c^{(i)}(x_i-\overline{x})(y_i-\overline{y})^T}
y = i = 0 ∑ L ω m ( i ) y i P y y = i = 0 ∑ L ω c ( i ) ( y i − y ) ( y i − y ) T P x y = i = 0 ∑ L ω c ( i ) ( x i − x ) ( y i − y ) T
采样策略
根据 Sigma 点采样策略不同,相应的 Sigma 点以及均值权值和方差权值也不尽相同,因此 UT 变换的估计精度也会有差异,但总体来说,其估计精度能够达到泰勒级数展开的二阶精度。为保证随机变量x经过采样之后得到的 Sigma 采样点仍具有原变量的必要特性,所以采样点的选取应满足下列条件:
g ( { x i , ω m ( i ) , ω c ( i ) } , L , P x ( x ) ) = 0 g(\{x_i,\omega_m^{(i)},\omega_c^{(i)}\},L,P_x(x))=0
g ( { x i , ω m ( i ) , ω c ( i ) } , L , P x ( x ) ) = 0
其中
{ x i , ω m ( i ) , ω c ( i ) } \{x_i,\omega_m^{(i)},\omega_c^{(i)}\} { x i , ω m ( i ) , ω c ( i ) } L 为采样点个数
P x ( x ) P_x(x) P x ( x ) g ( ) g() g ( ) P x ( x ) P_x(x) P x ( x )
g ( { x i , ω m ( i ) , ω c ( i ) } , L , P x ( x ) ) = [ ∑ i = 0 L ω m ( i ) − 1 ∑ i = 0 L ω c ( i ) − 1 ∑ i = 0 L w m ( i ) x i − x ‾ ∑ i = 0 L ω c ( i ) ( x i − x ‾ ) ( x i − x ‾ ) T − P x x ] = 0 g(\{x_i,\omega_m^{(i)},\omega_c^{(i)}\},L,P_x(x))=\begin{bmatrix}\sum_{i=0}^{L}\omega_m^{(i)}-1\\\sum_{i=0}^{L}\omega_c^{(i)}-1\\\sum_{i=0}^{L}w_m^{(i)}x_i-\overline{x}\\\sum_{i=0}^{L}{\omega_c^{(i)}(x_i-\overline{x})(x_i-\overline{x})^T}-P_{xx}\end{bmatrix}=0
g ( { x i , ω m ( i ) , ω c ( i ) } , L , P x ( x ) ) = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ ∑ i = 0 L ω m ( i ) − 1 ∑ i = 0 L ω c ( i ) − 1 ∑ i = 0 L w m ( i ) x i − x ∑ i = 0 L ω c ( i ) ( x i − x ) ( x i − x ) T − P x x ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ = 0
采样策略:比例采样
n 维随机变量 x 的均值和方差分别为 x ‾ \overline{x} x P x P_x P x
X ( i ) = { X ‾ i = 0 X ‾ + ( ( n + κ ) P ) i i = 1 ∼ n X ‾ − ( ( n + κ ) P ) i i = n + 1 ∼ 2 n ω m ( i ) = ω c ( i ) = { κ n + κ i = 0 κ 2 ( n + κ ) i = 1 ∼ 2 n X^{(i)}=\left\{\begin{aligned}&\overline{X}&&i=0\\&\overline{X}+(\sqrt{(n+\kappa )P})_i&&i=1\sim n\\&\overline{X}-(\sqrt{(n+\kappa) P})_i&&i=n+1\sim 2n\end{aligned}\right.\\\omega_m^{(i)}=\omega_c^{(i)}=\left\{\begin{aligned}&\frac{\kappa }{n+\kappa }&&i=0\\&\frac{\kappa }{2(n+\kappa )}&&i=1\sim 2n\end{aligned}\right.
X ( i ) = ⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ X X + ( ( n + κ ) P ) i X − ( ( n + κ ) P ) i i = 0 i = 1 ∼ n i = n + 1 ∼ 2 n ω m ( i ) = ω c ( i ) = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ n + κ κ 2 ( n + κ ) κ i = 0 i = 1 ∼ 2 n
其中
κ \kappa κ x ‾ \overline{x} x ( ( n + κ ) P ) i (\sqrt{(n+\kappa) P})_i ( ( n + κ ) P ) i ( n + κ ) P (n+\kappa) P ( n + κ ) P C h o l e s k y Cholesky C h o l e s k y
采样策略:比例修正对称采样
为保证协方差的半正定性以及解决采样的非局部效应问题,采用比例修正采样策略来近似非线性函数的后验分布
比例修正算法
x i ′ = x 0 + α ( x i − x 0 ) ( ω m ( i ) ) ′ = { ω m ( i ) α 2 + 1 − 1 α 2 i = 0 ω m ( i ) α 2 i ≠ 0 ( ω c ( i ) ) ′ = { ( ω m ( i ) ) ′ + ( 1 + β − α 2 ) i = 0 ( ω m ( i ) ) ′ i ≠ 0 x_i'=x_0+\alpha(x_i-x_0)\\(\omega_m^{(i)})'=\left\{\begin{aligned}&\frac{\omega_m^{(i)}}{\alpha^2}+1-\frac{1}{\alpha^2}&&i=0\\&\frac{\omega_m^{(i)}}{\alpha^2}&&i\not=0\end{aligned}\right.\\(\omega_c^{(i)})'=\left\{\begin{aligned}&(\omega_m^{(i)})'+(1+\beta-\alpha^2)&&i=0\\&(\omega_m^{(i)})'&&i\not=0\end{aligned}\right.
x i ′ = x 0 + α ( x i − x 0 ) ( ω m ( i ) ) ′ = ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ α 2 ω m ( i ) + 1 − α 2 1 α 2 ω m ( i ) i = 0 i = 0 ( ω c ( i ) ) ′ = { ( ω m ( i ) ) ′ + ( 1 + β − α 2 ) ( ω m ( i ) ) ′ i = 0 i = 0
其中 α \alpha α 0 ≤ α ≤ 1 0\leq\alpha\leq 1 0 ≤ α ≤ 1 α \alpha α β \beta β β = 2 \beta=2 β = 2
将上述比例修正算法带入对称采样中,得到比例修正对称采样策略
( X ( i ) ) ′ = { X ‾ i = 0 X ‾ + ( ( n + λ ) P ) i i = 1 ∼ n X ‾ − ( ( n + λ ) P ) i i = n + 1 ∼ 2 n ( ω m ( i ) ) ′ = { λ n + λ i = 0 λ 2 ( n + λ ) i = 1 ∼ 2 n ( ω c ( i ) ) ′ = { λ n + λ + ( 1 − α 2 + β ) i = 0 λ 2 ( n + λ ) i = 1 ∼ 2 n (X^{(i)})'=\left\{\begin{aligned}&\overline{X}&&i=0\\&\overline{X}+(\sqrt{(n+\lambda )P})_i&&i=1\sim n\\&\overline{X}-(\sqrt{(n+\lambda)P})_i&&i=n+1\sim 2n\end{aligned}\right.\\(\omega_m^{(i)})'=\left\{\begin{aligned}&\frac{\lambda}{n+\lambda}&&i=0\\&\frac{\lambda}{2(n+\lambda)}&&i=1\sim 2n\end{aligned}\right.\\(\omega_c^{(i)})'=\left\{\begin{aligned}&\frac{\lambda}{n + \lambda}+(1-\alpha^2+\beta)&&i=0\\&\frac{\lambda}{2(n+\lambda)}&&i=1\sim 2n\end{aligned}\right.
( X ( i ) ) ′ = ⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ X X + ( ( n + λ ) P ) i X − ( ( n + λ ) P ) i i = 0 i = 1 ∼ n i = n + 1 ∼ 2 n ( ω m ( i ) ) ′ = ⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ n + λ λ 2 ( n + λ ) λ i = 0 i = 1 ∼ 2 n ( ω c ( i ) ) ′ = ⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ n + λ λ + ( 1 − α 2 + β ) 2 ( n + λ ) λ i = 0 i = 1 ∼ 2 n
其中 λ = α 2 ( n + κ ) − n \lambda=\alpha^2(n+\kappa)-n λ = α 2 ( n + κ ) − n κ \kappa κ κ = 0 \kappa=0 κ = 0 κ = 3 − n \kappa = 3 - n κ = 3 − n ( n + λ ) P (n+\lambda)P ( n + λ ) P
状态方程与观测方程
X k + 1 = f ( X k ) + w k Z k = h ( X k ) + v k X_{k+1}=f(X_k)+w_k\\Z_k=h(X_k)+v_k
X k + 1 = f ( X k ) + w k Z k = h ( X k ) + v k
其中,
f f f h h h w , v w,v w , v
获得 2n+1 个采样组合(即Sigma点集)及其权值(n为需要估计的参数数量)
X ( i ) = { X ‾ i = 0 X ‾ + ( ( n + λ ) P ) i i = 1 ∼ n X ‾ − ( ( n + λ ) P ) i i = n + 1 ∼ 2 n X^{(i)}=\left\{\begin{aligned}&\overline{X}&&i=0\\&\overline{X}+(\sqrt{(n+\lambda )P})_i&&i=1\sim n\\&\overline{X}-(\sqrt{(n+\lambda)P})_i&&i=n+1\sim 2n\end{aligned}\right.
X ( i ) = ⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ X X + ( ( n + λ ) P ) i X − ( ( n + λ ) P ) i i = 0 i = 1 ∼ n i = n + 1 ∼ 2 n
其中 ( P ) T ( P ) = P (\sqrt{P})^T(\sqrt{P})=P ( P ) T ( P ) = P ( P ) i (\sqrt{P})_i ( P ) i
对上式进行整理
X k ∣ k ( i ) = [ X ^ k ∣ k X ^ k ∣ k + ( ( n + λ ) P k ∣ k ) i X ^ k ∣ k − ( ( n + λ ) P k ∣ k ) i ] X^{(i)}_{k|k}=\begin{bmatrix}\hat{X}_{k|k}\\\hat{X}_{k|k}+(\sqrt{(n+\lambda)P_{k|k}})_i\\\hat{X}_{k|k}-(\sqrt{(n+\lambda)P_{k|k}})_i\end{bmatrix}
X k ∣ k ( i ) = ⎣ ⎢ ⎡ X ^ k ∣ k X ^ k ∣ k + ( ( n + λ ) P k ∣ k ) i X ^ k ∣ k − ( ( n + λ ) P k ∣ k ) i ⎦ ⎥ ⎤
把这2n+1个点代进状态方程,获得了这些点的k+1步预测
X k + 1 ∣ k ( i ) = f ( k , X k ∣ k ( i ) ) X^{(i)}_{k+1|k}=f(k, X^{(i)}_{k|k})
X k + 1 ∣ k ( i ) = f ( k , X k ∣ k ( i ) )
根据上式得到的 2n+1 个预测结果,计算系统状态的 k+1 步预测均值和协方差矩阵
设计计算权重值
ω m ( i ) = { λ n + λ i = 0 λ 2 ( n + λ ) i = 1 ∼ 2 n ω c ( i ) = { λ n + λ + ( 1 − α 2 + β ) i = 0 λ 2 ( n + λ ) i = 1 ∼ 2 n \omega_m^{(i)}=\left\{\begin{aligned}&\frac{\lambda}{n+\lambda}&&i=0\\&\frac{\lambda}{2(n+\lambda)}&&i=1\sim 2n\end{aligned}\right.\\\omega_c^{(i)}=\left\{\begin{aligned}&\frac{\lambda}{n + \lambda}+(1-\alpha^2+\beta)&&i=0\\&\frac{\lambda}{2(n+\lambda)}&&i=1\sim 2n\end{aligned}\right.
ω m ( i ) = ⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ n + λ λ 2 ( n + λ ) λ i = 0 i = 1 ∼ 2 n ω c ( i ) = ⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ n + λ λ + ( 1 − α 2 + β ) 2 ( n + λ ) λ i = 0 i = 1 ∼ 2 n
其中 m 表示均值,c 表示协方差,上标为几个采样点,其中
λ = α 2 ( n + κ ) − n \lambda = \alpha^2(n+\kappa)-n λ = α 2 ( n + κ ) − n α \alpha α 0 ≤ α ≤ 1 0\leq\alpha\leq1 0 ≤ α ≤ 1 κ \kappa κ κ = 0 \kappa=0 κ = 0 κ = 3 − n \kappa = 3 - n κ = 3 − n ( n + λ ) P (n+\lambda)P ( n + λ ) P β \beta β β = 2 \beta =2 β = 2
下式的系统状态量的 k+1 步预测均值和协方差矩阵
X ^ k + 1 ∣ k = ∑ i = 0 2 n ω m ( i ) X k + 1 ∣ k ( i ) P k + 1 ∣ k = ∑ i = 0 2 n ω c ( i ) [ X k + 1 ∣ k ( i ) − X ^ k + 1 ∣ k ] [ X k + 1 ∣ k ( i ) − X ^ k + 1 ∣ k ] T + Q \hat{X}_{k+1|k}=\sum_{i=0}^{2n}\omega_m^{(i)}X^{(i)}_{k+1|k}\\P_{k+1|k}=\sum_{i=0}^{2n}\omega_c^{(i)}[X^{(i)}_{k+1|k}-\hat{X}_{k+1|k}][X^{(i)}_{k+1|k}-\hat{X}_{k+1|k}]^T+Q
X ^ k + 1 ∣ k = i = 0 ∑ 2 n ω m ( i ) X k + 1 ∣ k ( i ) P k + 1 ∣ k = i = 0 ∑ 2 n ω c ( i ) [ X k + 1 ∣ k ( i ) − X ^ k + 1 ∣ k ] [ X k + 1 ∣ k ( i ) − X ^ k + 1 ∣ k ] T + Q
根据上式的预测均值 X ^ k + 1 ∣ k \hat{X}_{k+1|k} X ^ k + 1 ∣ k P k + 1 ∣ k P_{k+1|k} P k + 1 ∣ k
X k + 1 ∣ k ( i ) = [ X ^ k + 1 ∣ k ( X ^ k + 1 ∣ k + ( n + λ ) P k + 1 ∣ k ) i X ^ k + 1 ∣ k − ( ( n + λ ) P k + 1 ∣ k ) i ] X^{(i)}_{k+1|k}=\begin{bmatrix}\hat{X}_{k+1|k}\\(\hat{X}_{k+1|k}+\sqrt{(n+\lambda)P_{k+1|k}})_i\\\hat{X}_{k+1|k}-(\sqrt{(n+\lambda)P_{k+1|k}})_i\end{bmatrix}
X k + 1 ∣ k ( i ) = ⎣ ⎢ ⎡ X ^ k + 1 ∣ k ( X ^ k + 1 ∣ k + ( n + λ ) P k + 1 ∣ k ) i X ^ k + 1 ∣ k − ( ( n + λ ) P k + 1 ∣ k ) i ⎦ ⎥ ⎤
将上式的点集带入观测方程,得到 k+1 步预测观测量
Z k + 1 ∣ k ( i ) = h ( X k + 1 ∣ k ( i ) ) Z_{k+1|k}^{(i)}=h(X_{k+1|k}^{(i)})
Z k + 1 ∣ k ( i ) = h ( X k + 1 ∣ k ( i ) )
上式能得到 2n+1 个预测结果,计算系统观测量的 k+1 步预测均值和协方差巨家镇,其中权值还是上面之前的权值
Z ‾ k + 1 ∣ k = ∑ i = 0 2 n ω m ( i ) Z k + 1 ∣ k ( i ) P z k z k = ∑ i = 0 2 n ω c ( i ) [ Z k + 1 ∣ k ( i ) − Z ‾ k + 1 ∣ k ] [ Z k + 1 ∣ k ( i ) − Z ‾ k + 1 ∣ k ] T + R P x k z k = ∑ i = 0 2 n ω c ( i ) [ X k + 1 ∣ k ( i ) − X ^ k + 1 ∣ k ] [ Z k + 1 ∣ k ( i ) − Z ‾ k + 1 ∣ k ] T \overline{Z}_{k+1|k}=\sum_{i=0}^{2n}\omega_m^{(i)}Z_{k+1|k}^{(i)}\\P_{z_kz_k}=\sum_{i=0}^{2n}\omega_c^{(i)}[Z_{k+1|k}^{(i)}-\overline{Z}_{k+1|k}][Z_{k+1|k}^{(i)}-\overline{Z}_{k+1|k}]^T+R\\P_{x_kz_k}=\sum_{i=0}^{2n}\omega_c^{(i)}[X_{k+1|k}^{(i)}-\hat{X}_{k+1|k}][Z_{k+1|k}^{(i)}-\overline{Z}_{k+1|k}]^T
Z k + 1 ∣ k = i = 0 ∑ 2 n ω m ( i ) Z k + 1 ∣ k ( i ) P z k z k = i = 0 ∑ 2 n ω c ( i ) [ Z k + 1 ∣ k ( i ) − Z k + 1 ∣ k ] [ Z k + 1 ∣ k ( i ) − Z k + 1 ∣ k ] T + R P x k z k = i = 0 ∑ 2 n ω c ( i ) [ X k + 1 ∣ k ( i ) − X ^ k + 1 ∣ k ] [ Z k + 1 ∣ k ( i ) − Z k + 1 ∣ k ] T
计算Kalman增益矩阵
K k + 1 = P x k z k P z k z k − 1 K_{k+1}=P_{x_kz_k}P_{z_kz_k}^{-1}
K k + 1 = P x k z k P z k z k − 1
更新系统状态与协方差 P
X ^ k + 1 ∣ k + 1 = X ^ k + 1 ∣ k + K k + 1 [ Z k + 1 − Z ‾ k + 1 ∣ k ] P k + 1 ∣ k + 1 = P k + 1 ∣ k − K k + 1 P z k z k K k + 1 T \hat{X}_{k+1|k+1}=\hat{X}_{k+1|k}+K_{k+1}[Z_{k+1}-\overline{Z}_{k+1|k}]\\P_{k+1|k+1}=P_{k+1|k}-K_{k+1}P_{z_kz_k}K^T_{k+1}
X ^ k + 1 ∣ k + 1 = X ^ k + 1 ∣ k + K k + 1 [ Z k + 1 − Z k + 1 ∣ k ] P k + 1 ∣ k + 1 = P k + 1 ∣ k − K k + 1 P z k z k K k + 1 T
其中 Z k + 1 Z_{k+1} Z k + 1
最终小结
UKF 用UT变换近似逼近了系统非线性变换后的分布,得到的 Kalman 增益可以类比成状态变量X的在当前步的线性修正率,有了这个线性修正率再去×修正量(实测-预测均值,即 Z k + 1 − Z ‾ k + 1 ∣ k Z_{k+1}-\overline{Z}_{k+1|k} Z k + 1 − Z k + 1 ∣ k