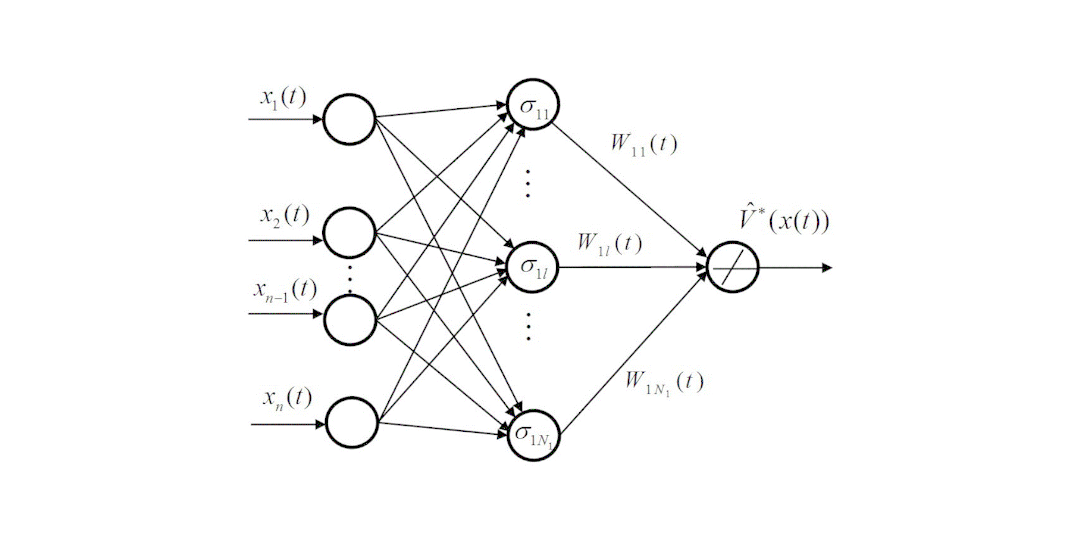
PF粒子滤波器
前言
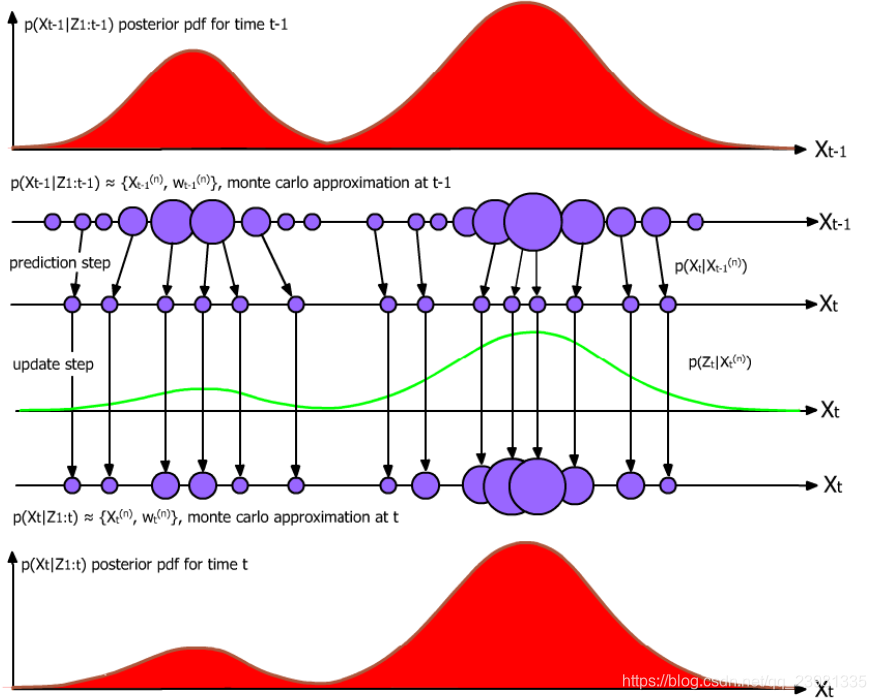
对于一般的非线性/非高斯系统,解析求解的途径是行不通的。在数值近似方法中,蒙特卡罗仿真是一种最为通用、有效的手段,粒子滤波就是建立在蒙特卡罗仿真基础之上的,它通过利用一组带权值的系统状态采样来近似状态的统计分布。由于蒙特卡罗仿真方法具有广泛的适用性,由此得到的粒子滤波算法也能适用于一般的非线性/非高斯系统。但是,这种滤波方法也面临几个重要问题,如有效采样(粒子)如何产生、粒子如何传递以及系统状态的序贯估计如何得到等。
简单的理解,粒子滤波就是使用了大量的随机样本,采用 蒙特卡洛(MonteCarlo,MC)仿真技术完成 贝叶斯递推滤波 (Recursive Bayesian Filter) 过程。
一阶矩 mean
一阶矩是随机变量的期望值
μ=E[X]=∑p(xi)xi\mu=E[X]=\sum p(x_i)x_i
μ=E[X]=∑p(xi)xi
二阶矩 variance
二阶矩是随机变量偏离其期望值的平方的期望值,表示随机变量的离散程度
σ2=E[(X−μ)2]=∑p(xi)(xi−μ)2\sigma^2=E[(X-\mu)^2]=\sum p(x_i)(x_i-\m ...
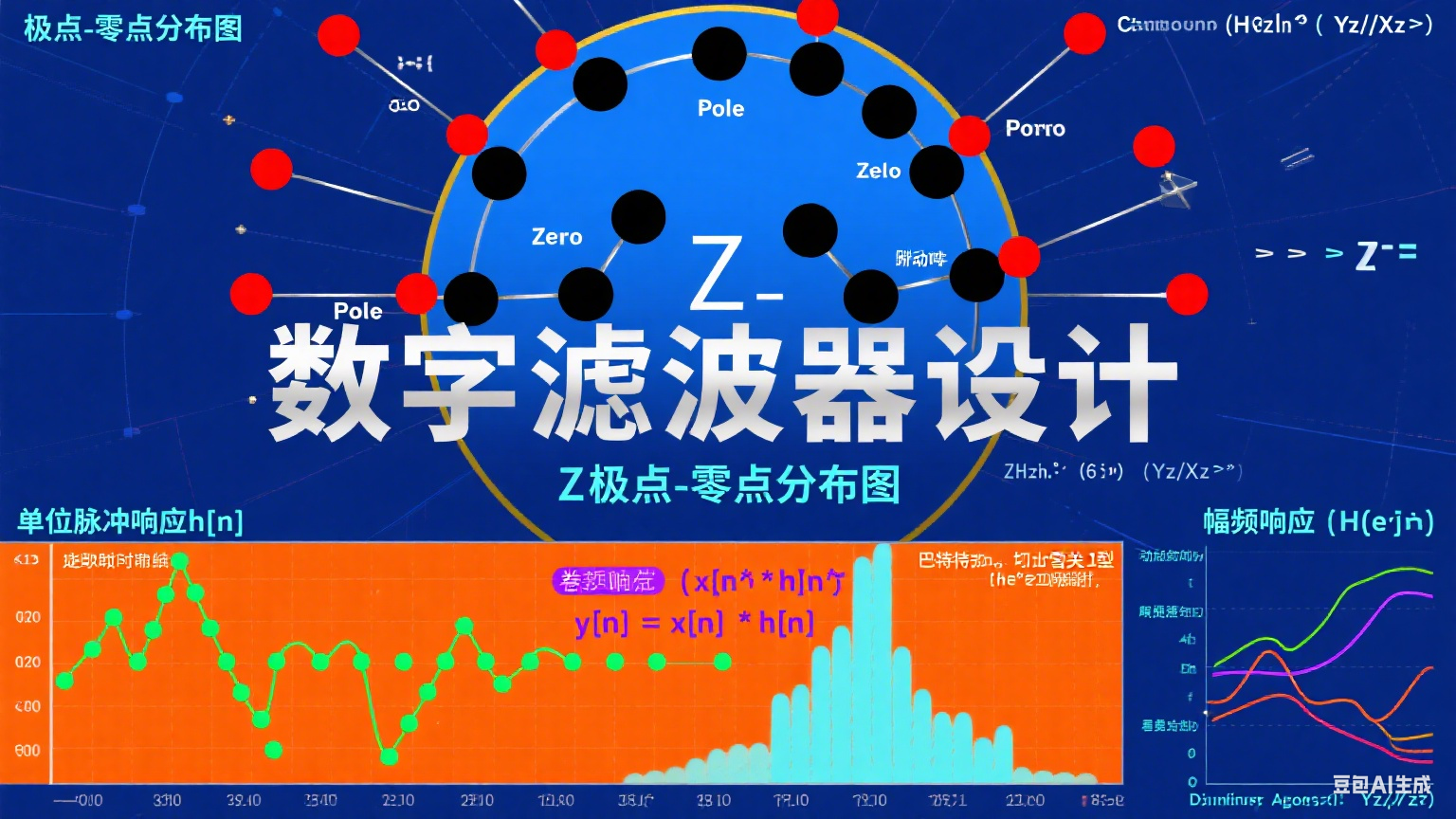
数字滤波器
数字滤波器
数字滤波器按照最佳逼近特性可以分为巴特沃斯Butterworth,切比雪夫Chebyshev,贝塞尔Bessel,椭圆Elliptic滤波器。按照频带又可以分为低通,高通,带通,带阻滤波器,其中高通,带通和带阻滤波器都可以由低通滤波器由频率变换得到。
低通滤波器
当输入信号频率小于某一截止频率时,低通滤波器能够通过信号,使其保留低频分量,而将高于截止频率的部分信号阻止或者减弱
传递函数为
G(s)=G0wcn(s+wc)nG(s)=\frac{G_0w_c^n}{(s+w_c)^n}
G(s)=(s+wc)nG0wcn
这就是 n 阶低通滤波的传递函数,其中 wcw_cwc 就是截至频率, G0G_0G0 是通带增益或零频增益
高通滤波器
当输入信号频率大于某一截止频率时,高通滤波器能够通过信号,使其保留高频分量,而将低于截止频率的部分信号阻止或者减弱
传递函数为
G(s)=G0wcnsn(s+wc)nG(s)=\frac{G_0w_c^ns^n}{(s+w_c)^n}
G(s)=(s+wc)nG0wcnsn
这就是 n 阶高通滤波的传递函数,其中 wc ...
QP二次规划
一些定义
对于一个函数 F:Rn→RmF:R^n→R^mF:Rn→Rm 是一个将欧式 n 维空间的函数,该函数由 m 个实函数构成, y1(x1,…,xn),…,ym(x1,…,xn)y_1(x_1,…,x_n),…,y_m(x_1,…,x_n)y1(x1,…,xn),…,ym(x1,…,xn)
Jacobian 矩阵
函数 F 的偏导数组成一个 m 行 n 列的矩阵,就是 Jacobian 矩阵
JF(x1,...,xn)=[∂y1∂x1...∂y1∂xn.........∂ym∂x1...∂ym∂xn]J_F(x_1,...,x_n)=\begin{bmatrix}\frac{\partial y_1}{\partial x_1}&...&\frac{\partial y_1}{\partial x_n}\\...&...&...\\\frac{\partial y_m}{\partial x_1}&...&\frac{\partial y_m}{\partial x_n}\end{bmatrix}
JF(x1,... ...
贝叶斯滤波
前言
在时移系统中通过对带有噪声的观测来估计隐状态的处理方法,滤波专门是指利用前面 k 个观测 y1,y2,…,yky_1,y_2,…,y_ky1,y2,…,yk 来估计第 k 个隐状态 xkx_kxk 的方法,记作 xk∣y1:kx_k|y_{1:k}xk∣y1:k
如果利用前 d 个观测 (d<k) 来估计第 k 个状态,称为预报
如果利用前 d 个观测 (d>k) 来估计第 k 个状态。则称为平滑或内插
所以实际的滤波是 d=kd=kd=k 的情形,本质上就是观测 yky_kyk 已知并且带有噪声,用它来估计未知隐状态 xkx_kxk
马尔可夫过程
贝叶斯滤波
状态空间模型
对于一个可观测的系统,可以得到
xk=Axk−1+Buk+Gwkyk=Cxk+vkx_k=Ax_{k-1}+Bu_k+Gw_k\\y_k=Cx_k+v_k
xk=Axk−1+Buk+Gwkyk=Cxk+vk
其中 wk,vkw_k,v_kwk,vk 分别是过程噪声和观测噪声,并且上式为状态空间方程的状态方程,下式为测量方程
模型假设
由于跟踪设备获得的量测信 ...
PR比例谐振控制器
github仓库
比例谐振控制算法分析 - 百度文库 (baidu.com)
前言
在传统的矢量控制系统中,广泛的采用了坐标变换技术,将三相静止坐标系下的电流电压等正弦量转化为同步旋转坐标系下的直流量,这个实现了简化系统,并且能够很好的使电机实现解耦控制。这么做的原因就是 PI 控制器无法对正弦量实现无静差控制,坐标变换简化了系统外环控制的设计,却造成内环结构复杂,设计困难。而且在电机运行中,电机的电感,电阻等电机参数会随着磁路的饱和,温度的升高而发生改变,从而使交叉耦合项不准确,进而使系统的控制精度下降。
PR 控制器可以实现对交流的无静差控制,将 PR 控制器用于网侧变换器的控制系统中,可以在两个相对静止的坐标系下对电流进行调节,可以简化控制过程中的坐标变换,消除电流 d,q 轴分量之间的耦合关系,并且可以忽略电网电压对系统的扰动作用。并且使用 PR 控制器更容易实现低次滤波补偿,这些都有利于简化系统的结构
傅里叶变换
F(ω)=∫−∞∞f(t)e−jωtdtf(t)=12π∫−∞∞F(ω)ejωtdωF(\omega)=\int_{-\infty}^{\infty}f(t)e^{ ...
卡尔曼滤波
github仓库
卡尔曼滤波 KF
公式
x^k∣k−1=Fkx^k−1∣k−1Pk∣k−1=FkPk−1∣k−1FkT+QkKk=Pk∣k−1HkT(HkPk∣k−1HkT+Rk)−1x^k∣k=x^k∣k−1+Kk(zk−Hkx^k∣k−1)Pk∣k=(I−KkHk)Pk∣k−1\hat{x}_{k|k-1}=F_k\hat{x}_{k-1|k-1}\\P_{k|k-1}=F_kP_{k-1|k-1}F_k^T+Q_k\\K_k=P_{k|k-1}H_k^T(H_kP_{k|k-1}H_k^T+R_k)^{-1}\\\hat{x}_{k|k}=\hat{x}_{k|k-1}+K_k(z_k-H_k\hat{x}_{k|k-1})\\P_{k|k}=(I-K_kH_k)P_{k|k-1}
x^k∣k−1=Fkx^k−1∣k−1Pk∣k−1=FkPk−1∣k−1FkT+QkKk=Pk∣k−1HkT(HkPk∣k−1HkT+Rk)−1x^k∣k=x^k∣k−1+Kk(zk−Hkx^k∣k−1)Pk∣k=(I−KkHk)Pk∣k−1
基本 ...
最优控制
一个最优的控制策略是无论最初状态和最初的决策是什么,剩余的控制策略一定符合最优控制策略
需要考虑的问题
性能指标
假设一个系统中的状态量分别为 x1,…,xnx_1,…,x_nx1,…,xn,并且期望值 x1d,…,xndx_{1d},…,x_{nd}x1d,…,xnd ,可以得到性能指标,这里的状态量指的是一个状态在不同的时间下的具体表现
J=(x1−x1d)2+...+(xn−xnd)2J=(x_1-x_{1d})^2+...+(x_n-x_{nd})^2
J=(x1−x1d)2+...+(xn−xnd)2
体现的是每个状态变量的代价,也就是代价函数,当 J→0J→0J→0 也就是说明状态与期望状态越接近,上式还可以写作另一种形式,令 en=xnd−xne_n=x_{nd}-x_nen=xnd−xn
J=[e1...en][e1...en]J=\begin{bmatrix}e_1&...&e_n\end{bmatrix}\begin{bmatrix}e_1\\...\\e_n\end{bmatrix}
J=[e1...en]⎣⎢⎡e ...
ADRC自抗扰控制器
github仓库
前言
为了解决快速性和超调的矛盾,在控制器设计过程中引入了过渡过程,通俗的讲就是输入信号从初始值到目标值并不是阶跃的,而是平滑过渡的,并且这个过渡过程的时间长短是可以调节的。将过渡过程和微分器在一个模块中实现,称为**跟踪-微分器(TD),**单独的过渡过程和速度规划并没有本质区别。但是TD和速度规划不是一回事,TD将输入过渡和微分器统一为一个模块,它一边尽可能快地跟踪输入信号,同时给出输入信号近似的微分。
自抗扰控制对扰动和不确定性的处理是自抗扰控制最突出的特征,它把作用于被控对象的所有不确定因素都归结为“未知扰动”,而用被控对象的输入输出数据对它进行估计,并给予补偿。“自抗扰”的名称也来源于此,即主动抵抗干扰,不需要直接测量外扰的作用,也不需要实现知道扰动的规律(能知道更好)。构建观测器,利用被控对象的输入、输出和所施加的控制输入来估计作用于系统的总扰动(包括内扰和外扰,可以粗浅地理解为所有的影响因素),实现这一功能的模块被称为扩展状态观测器(Extended State Observer,ESO)。这个名字也与观测器的形式十分匹配,因为在设计ESO时,首先构造 ...
LQG线性二次高斯
github仓库
前言
Linear Quadratic Gaussian
在实际系统中,噪声是不可避免的,在噪声的影响下,系统状态方程可以写作
{X˙=AX+Bu+Gwy=CX+Du+Hw+v\left\{\begin{aligned}&\dot{X}=AX+Bu+Gw\\&y=CX+Du+Hw+v\end{aligned}\right.
{X˙=AX+Bu+Gwy=CX+Du+Hw+v
其中 w,vw,vw,v 均被当作为白噪声
如果我们假设噪声是均值为0高斯分布(事实上很多时候确实近似服从高斯分布,想想为什么呢?)由于系统噪声和输出噪声的存在,状态不能完美的衰减为0。我们就希望优化损失函数的期望,即
J=E{limT→∞1T∫0T[XTQX+UTRU]dt}J=E\{\underset{T\rightarrow\infty}{\lim}\frac{1}{T}\int_0^T[X^TQX+U^TRU]dt\}
J=E{T→∞limT1∫0T[XTQX+UTRU]dt}
LQG 控制器实际上就是一个最优二次型线性调节器+一个最优状态估计器(卡尔曼滤波器)而 ...
WBC全身控制器
前言
概述
在 WBC 的各种功能中,任务层次结构很重要,因为它提供了一个保证,即较高的优先级任务不会由于与较低优先级任务的冲突而失败。 该方法类似于资源分配问题,其中一些资源(即机器人附件或部件)比其他部件更重要,同时试图实现多个目标。
伪逆矩阵
伪逆矩阵又叫做广义逆矩阵,是线性代数中针对矩阵的一种运算,指的是拥有部分逆矩阵的特性,但是不一定具有逆矩阵的所有特性的另一种矩阵。
假设
A∈Rn×mAg∈Rm×nA\in R^{n\times m}\\A^g\in R^{m\times n}
A∈Rn×mAg∈Rm×n
并且满足
AAgA=AAA^gA=A
AAgA=A
则 AgA^gAg 就是 AAA 的广义逆矩阵。
建构广义逆阵的目的是针对可逆矩阵以外的矩阵(例如非方阵的矩阵)可以找到一矩阵有一些类似逆矩阵的特性。任意的矩阵都存在广义逆阵,若一矩阵存在逆矩阵,逆矩阵即为其唯一的广义逆阵。
伪逆矩阵的性质
AAgA=AAgAAg=AgAAg=(AAg)TAgA=(AgA)TAA^gA=A\\A^gAA^g=A^g\\AA^g=(AA^g)^T\\A^gA=(A^gA)^T
AAgA=A ...
鲁棒控制理论
前言
一种典型的不确定系统模型的基本形式是
y=(P+Δ)u+ny=(P+\Delta)u+n
y=(P+Δ)u+n
其中,y 是系统输出,u 是系统输入,P 是标称对象的传递函数,模型的不确定性以两种形式展现:n 是未知噪声或者干扰, Δ\DeltaΔ 是位置的对象摄动(未建模动态)
一般地说,鲁棒性概念是指反馈控制系统的某项性能对于某集合中的每一个对象都是成立的。具体地说,我们有如下鲁棒性定义。
鲁棒稳定性:设计一个控制器,使对每一个摄动后的对象,都能保证闭环系统的稳定性。
鲁棒性能:设计一个控制器,使对每一个摄动后的对象,闭环系统都满足稳定性和某种特定的系统性能。
上述鲁棒性的概念是指定给定一个控制器,如果某集合中的每一个对象都能保持某种特性成立,则称控制器对此特性是鲁棒的。因此鲁棒性必须包含一个控制器,有一个对象的集合和某些系统的特性
H∞H_\inftyH∞ 控制器
一些定义
首先说明一些定义
supsupsup:一个集合最小的上界,不小于它最大值的值,都是它的上界
infinfinf:一个集合最大的下界,不大于它最小值的值,都是它的下界
maxmaxmax ...
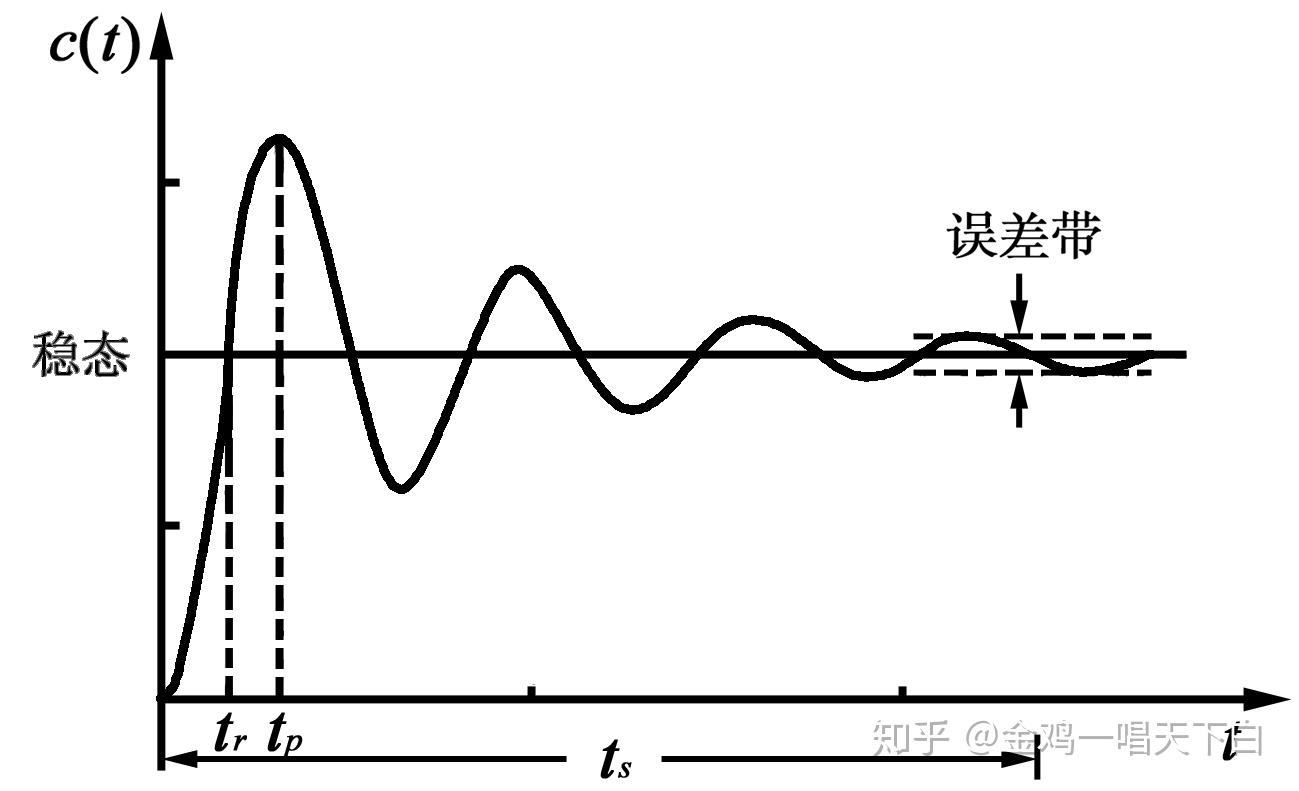
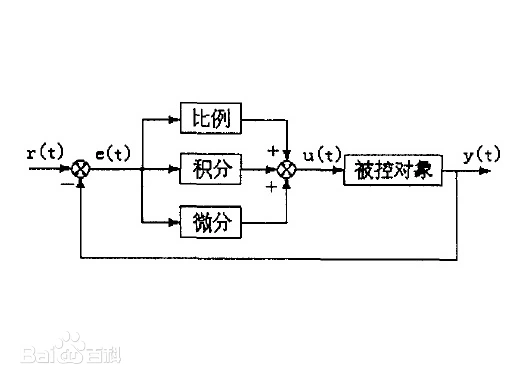
PID控制理论
github仓库
完整计算公式
output=kperrnow+ki∑j=0kej+kd(errnow−errlast)output=k_perr_{now}+k_i\sum_{j=0}^{k}e_j+k_d(err_{now} - err_{last})
output=kperrnow+kij=0∑kej+kd(errnow−errlast)
含义:
P: kperrnowkperr_{now}kperrnow
就是 kp 乘以此次误差,理论值与当前值的差值,作用是主动减小误差,使测量值主动贴近理论值。但是如果只有P的话,响应可能会非常剧烈,不好把控,P太大会导致超调
I: ki∑j=0kejki\sum_{j = 0}^{k} e_jki∑j=0kej
只要存在误差(稳态误差),不论误差有多小,i的输出也会越来越大
作用是消除稳态误差,当系统误差已经接近0时,p 的输出会很小,起不到继续减小误差的作用了,导致误差没有办法减小到0,这个时候就需要用到 I 算法,让误差值不断累积,并且累加到输出中
D: kd(errnow−errlast)kd(err ...
数字信号和模拟信号
模拟信号(Analog signal)简称 A
模拟信号是连续的信号,如下图中红色的曲线
优点
更容易处理
最适合音频和视频传输
具有更高的密度,可以传输更精细的信息
需要的带宽比数字信号少
可以准确的表达物理现象的变化
电气容差敏感度较低
缺点
长距离传输可能会产生意外干扰信号
容易产生耗损
数字信号抗扰性更高,模拟信号更容易受到噪声和失真的影响
信号质量较低
数字信号(Digital signal)简称 D
数字信号是离散的信号,如下图中黑色的阶梯型曲线
优点
能以更小的噪声,失真和干扰传递信息
数字电路能以较低的成本更容易大量复制
数字信号处理更加灵活,因为通过数字可编程系统可以改动DSP的操作
数字信号处理更加安全,数字信号可以被轻易加密和压缩
数字系统更加精确,而且通过错误检测和矫正代码可以降低错误发生的几率
数字信号可以通过半导体芯片存储在任何磁性介质或者光学介质上
数字信号可以远距离传输
缺点
与传输相同信息的模拟信号相比,数字通信需要更高的带宽
DSP以更高的速率处理信号,而且包含更多上层内部硬件资源,这将导致更高的功耗,而模拟信号处理因为包含消耗更少能量 ...
FOC磁场定向控制
电机场向量调制是一种用于控制感应电机的方法。它使用三相电流控制来调制电机的转矩和转速。在FOC控制中,电机的转子位置和速度被监测和估计,以提供准确的电流控制。这使得电机能够以高效率和低噪音运行。
FOC控制是现代驱动器系统的标准,用于控制感应电机、同步电机和永磁电机。它提供了高度可预测的电机控制,并且可以在不同负载条件下实现高效率。
电机类型
步进电机
步进电机是一种将电脉冲转化为角位移的执行机构。通俗一点讲当步进驱动器接收到一个脉冲信号,它就驱动步进电机按设定的方向转动一个固定的角度(及步进角)。您可以通过控制脉冲个数来控制角位移量,从而达到准确定位的目的;同时您可以通过控制脉冲频率来控制电机转动的速度和加速度,从而达到准确定位的目的;同时您可以通过控制脉冲频率来控制电机转动的速度和加速度,从而达到调速的目的。
永磁式 一般为2相,转矩和体积比较小,步进角为7.5或者15度
反应式 一般为3相,可实现大扭矩,步进角1.5度,噪声振动较大
混合式 结合以上两者优点,分为2相和5相,步进角为1.8度和0.72度
直流电机 通入直流旋转,反向电流就反向转
交流电机 输入或 ...
阻抗和导纳控制
机器人交互控制
直接力控 直接对完成任务所需要的力做一个设定,利用力或者转矩的传感器实时对力进行反馈,从而达到控制
存在的一些问题:使用的一些力的传感器一般会比较贵,也会出现精度和噪声的情况,其次就是不容易对力进行设定
间接力控
柔顺控制
被动柔顺 使用一些机械的设备,例如弹簧之类的设备使机器人在与外界交互中出现一些柔顺性
主动柔顺 通过软件使机器人对外界的环境做出一些柔顺性
阻抗/导纳控制 让机器人在与外界交互的过程中,包含有质量,弹簧,阻尼这样一个二阶阻抗系统的性质
关节空间
笛卡尔空间 也就是三维空间坐标系
力位混合控制
机器人在某个方向上做力的控制,在正交的方向上做位移的控制
阻抗控制
关节空间内的阻抗控制
目标:让机器人的每一个关节能体现出由弹簧-阻尼-质量组成的二阶系统的动态特性,其中 qdq_dqd 是对关节角度的设定值, qqq 是实际测量值,那么 q‾\overline{q}q 就是一个控制误差,左边就是对这个控制的动态误差的描述,M, D, K 就是三个矩阵,表示质量,阻尼和弹性系数,这个q矩阵的大小是和关节数自由度量有关的 ...
VMC虚拟模型控制
一点点小补充
M3508 转矩常数0.3,也就是每增加1A电流力矩增加0.3牛米
AK80-6 转矩常数 0.09 这个好像不用管
对于四足,电机相对,力矩Tp由TB和TF共同提供,会比以上计算更简单
五连杆正运动学解算
以杆 L5L_5L5 的中心为原点,可以得到
A=(−L52,0)B=(−L52+L1cosφ1,L1sinφ1)D=(L52+L4cosφ4,L4sinφ4)E=(L52,0)A=(-\frac{L_5}{2}, 0)\\B=(-\frac{L_5}{2}+L_1\cos\varphi_1,L_1\sin\varphi_1)\\D=(\frac{L_5}{2}+L_4\cos\varphi_4,L_4\sin\varphi_4)\\E=(\frac{L_5}{2},0)
A=(−2L5,0)B=(−2L5+L1cosφ1,L1sinφ1)D=(2L5+L4cosφ4,L4sinφ4)E=(2L5,0)
通过五连杆左右两部分列写 C 点坐标,可以得到下列等式
{xB+L2cosφ2=xD+L3cosφ3yB+L2si ...
HighGain and HighFrequency
github仓库
控制器原理
对于一个系统
x˙=f(x)+ux→xd\dot{x}=f(x)+u\\\\
x\rightarrow x_d
x˙=f(x)+ux→xd
其中不清楚 f(x)f(x)f(x) 的具体表达形式,但是 f(x)f(x)f(x) 是有界的,并且 ∣f(x)∣<ρ(x)|f(x)|<\rho(x)∣f(x)∣<ρ(x) ,引入误差 e=xd−xe=x_d-xe=xd−x ⇒ e˙=x˙d−f(x)−u\dot{e}=\dot{x}_d-f(x)-ue˙=x˙d−f(x)−u,定义李雅普诺夫函数 V(e)=12e2V(e)=\frac{1}{2}e^2V(e)=21e2 ,不妨令
u=ke+x˙d+uauxu=ke+\dot{x}_d+u_{aux}
u=ke+x˙d+uaux
其中 uauxu_{aux}uaux 是一个辅助的控制器,但是使用滑膜控制器 uaux=ρ(x)∣e∣eu_{aux}=\rho(x) \frac{|e|}{e}uaux=ρ(x)e∣e∣,而这个会导致系统不断抖动
High Gain
控制器的具体形式为 ...
SMC滑膜控制理论
github仓库
李雅普诺夫Lyapunov平衡理论
李雅普诺夫(第二方法)稳定性
如何理解李雅普诺夫稳定性分析
主要是用来判断一个系统是否能稳定
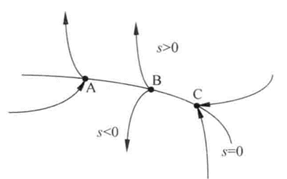
平衡点
一个控制系统最重要的问题就是稳定性的问题。稳定性就是一个系统在收到扰动之后能否有能力在平衡状态继续工作。平衡点就是系统状态不再发生状态的点,可能不止一个,也可能很脆弱稍微有点扰动就不再平衡了。实际上系统状态稳定的点应该是导数为0的点,也就是让系统状态方程的所有状态的导数为0,即变化率为0。
李雅普诺夫稳定
如果平衡状态受到扰动之后,仍然停留在平衡状态点附近,即该平衡点在李雅普诺夫意义下是稳定的
如果平衡状态受到扰动之后,最终都会收敛到该平衡点处,即该平衡点在李雅普诺夫意义下是渐进稳定的
如果平衡状态受到任何扰动之后最终都会收敛到该平衡点处时,即该平衡点咋子李雅普诺夫意义下是大范围渐进稳定的
如果平衡状态受到某种扰动之后状态开始偏离平衡点,就称该点在李雅普诺夫意义下是不稳定的
李雅普诺夫第一法
需要将非线性系统在平衡态附近线性化,然后讨论线性化系统的特征值分布来研究原非线性系统的稳定性问题。称之为间接法
李雅普诺 ...