单调栈

用于寻找一个数组内最大或者最小的元素，单调的意思就是栈内的数据排列是单调递增或者递减的

例如，如果是一个单调递增的栈，遇到比top元素更小的元素的话，就需要把top之前比该元素小的元素全部弹出，之后再将该元素放入，继续维持单调栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// leetcode 42
int trap(vector<int>& height)
{
 stack<int> stack;
 int     n   = height.size();
 int     res = 0;
 for (int i = 0; i < n; i++) {
  // 将栈顶中小的元素推出栈，并且计算这个范围内的数据
  while (!stack.empty() && stack.top() < height[i]) {
   int top = stack.top();
   stack.pop();
   if (!stack.empty()) // 如果已经空了就中断不再进行下列的操作 说明已经计算完所有的数据了
    break;
   int left     = stack.top();
   int currentwidth   = i - left - 1;
   int currentheight  = min(height[left], height[i]) - height[stack.top()];
   res      += currentwidth * currentheight;
  }
  // 将数据进栈
  stack.push(i);
 }
 return res;
}

回溯算法

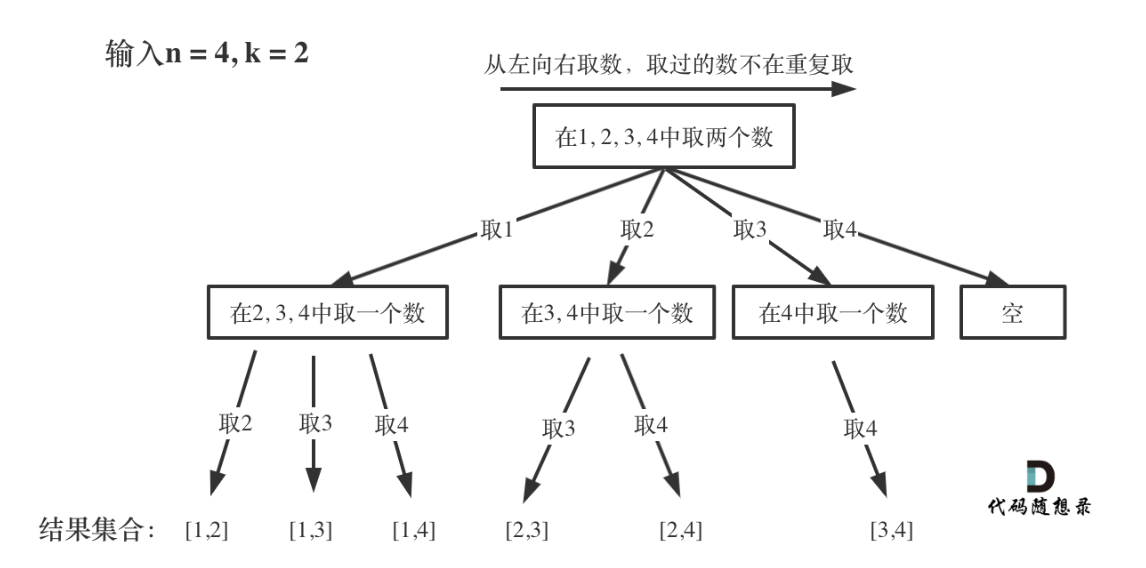
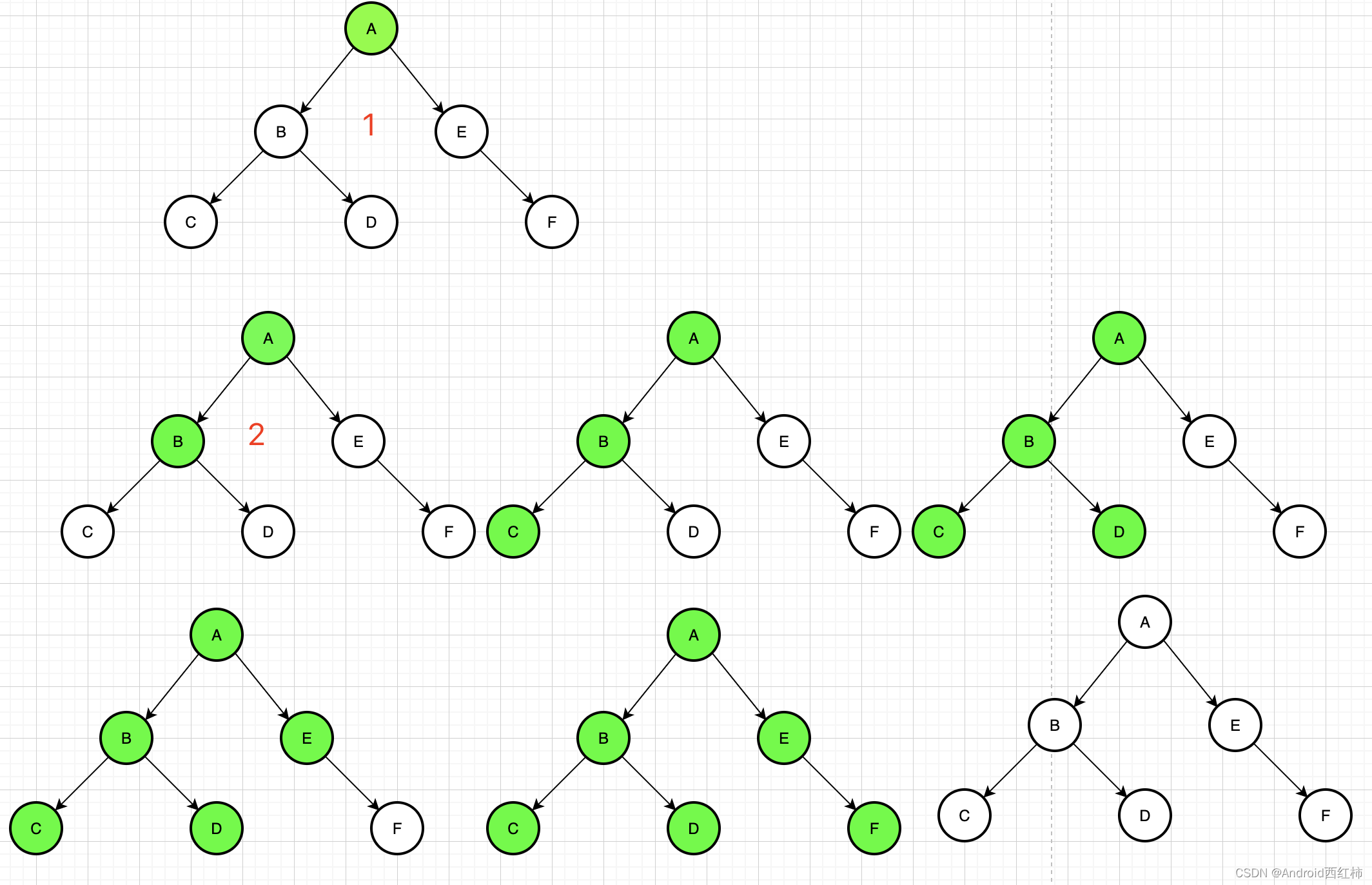
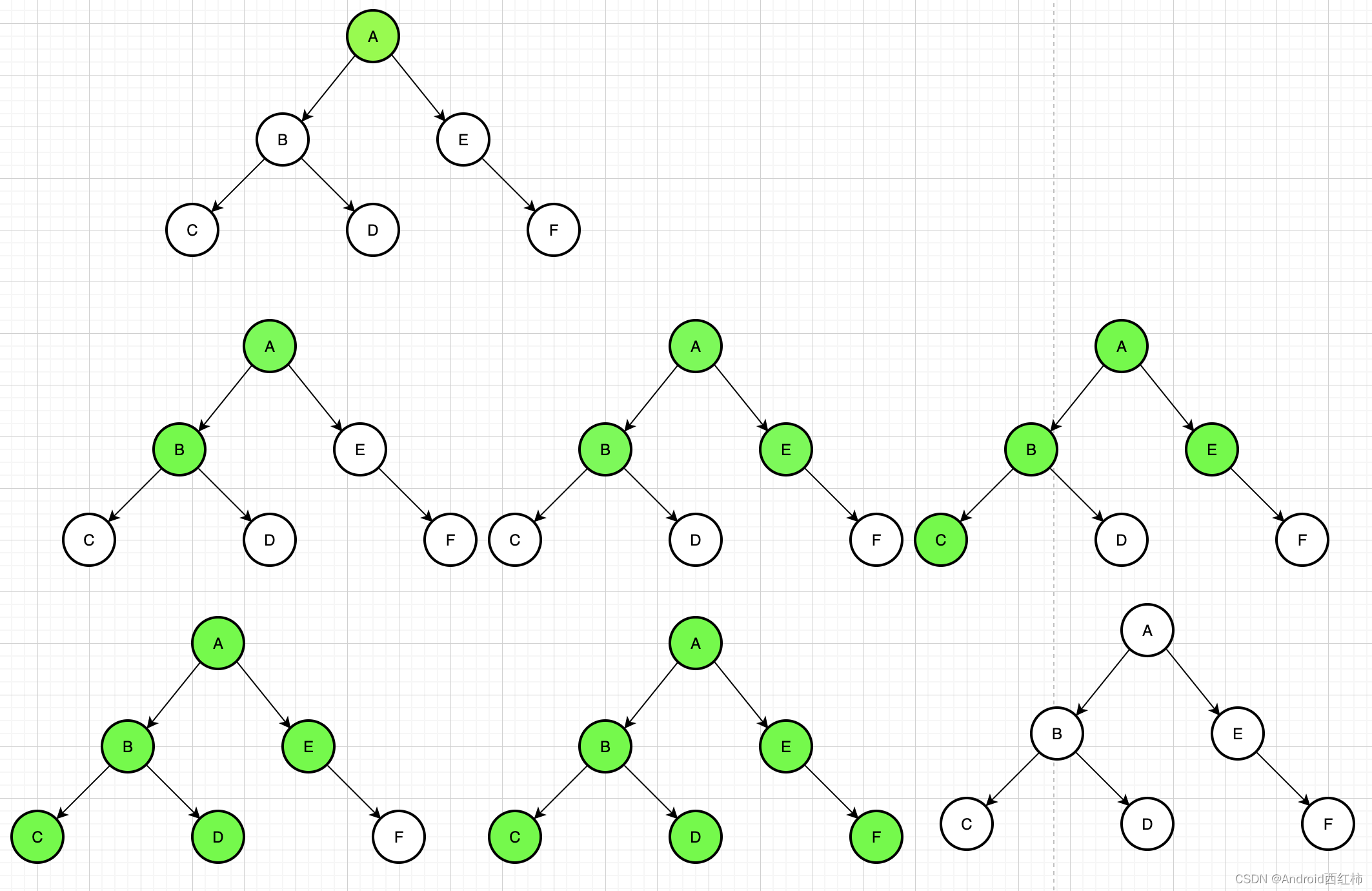
回溯算法的结构可以抽象为树形结构，N叉树

1671680280-ucUOKd-image.png

每次从集合中选取元素，可以选择的范围就会缩小，图中，n就是树的宽度，k就是树的深度，每次都搜索到叶子节点，就可以找到一个结果

回溯算法三部曲

  • 递归函数的返回值和参数

    需要定义两个全局变量，一个用来存储符合的结果，一个用于存储单次的结果，这样的话代码的可读性就比较好，有时候会定义开始位置来防止出现重复的结果

  • 回溯的终止条件

    当每次回溯从开始位置已经不可能满足结果的条件了，就可以终止本次回溯，这个终止条件相当于是剪枝优化。

    当寻找到符合条件的结果之后，就可以终止本次回溯，也就是说，会回到上一层回溯的状态，然后跳过这一个元素并且继续回溯。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
vector<string> letterCombinations(string digits)
{
 vector<string> res;
 callBack(res, digits);
 return res;
}
char map[10][4] = {
 {' ', ' ', ' ', ' '},
   {' ', ' ', ' ', ' '},
 {'a', 'b', 'c', ' '},
   {'d', 'e', 'f', ' '},
 {'g', 'h', 'i', ' '},
 {'j', 'k', 'l', ' '},
   {'m', 'n', 'o', ' '},
 {'p', 'q', 'r', 's'},
   {'t', 'u', 'v', ' '},
 {'w', 'x', 'y', 'z'},
};
void callBack(vector<string>& numbers, string digits)
{
 if (digits.length() == 0)
  return;
 int sl = 3;
 if (digits[0] - 0x30 == 7 || digits[0] - 0x30 == 9)
  sl = 4;
 int n = numbers.size();
 if (n == 0) {
  string s = "";
  for (int j = 0; j < sl; j++) { numbers.emplace_back(s + map[digits[0] - 0x30][j]); }
 } else
  for (int i = 0; i < n; i++) {
   for (int j = 0; j < sl; j++) { numbers.emplace_back(numbers[i] + map[digits[0] - 0x30][j]); }
  }
 numbers.erase(numbers.begin(), numbers.begin() + n);
 callBack(numbers, string(digits.begin() + 1, digits.end()));
}

贪心算法 Greedy

在对问题求解的时候，总是作出当前来看最优的解，不从整体上考虑，只求的局部最优解

KMP算法

kmp相当于是双指针，对于需要匹配的字符串c2和目标字符串c1，next数组记录的是c1字符串与c2字符串不匹配的时候下一次的位置，这个next数组的记录一定需要寻找之前的与当前字符串相等的位置，并且需要回溯的时候回到那个位置。

next[i-1] 表示当前不匹配的话返回的上一个位置。如果返回的位置与当前的位置一直不相同就一直返回到开头，next[i-1] 就是如果有循环的字符串的话，返回到的上一次循环的位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
int kmp(string c1, string c2)
  {
    int len1 = c1.length();
    int len2 = c2.length();
    int next[len1];
    next[0] = 0;
    int k = 0;
    for (int i = 1; i < len1; i++)
    {
      while (k > 0 && c1[i] != c1[k])
        k = next[k - 1];
      if (c1[i] == c1[k]) 
        k++;
      next[i] = k; // 记录与之相等的最相近的坐标位置
    }
    for (int i = 0, j = 0; i < len1; i++)
    {
      while (j > 0 && c1[i] != c2[j])
        j = next[j - 1];
      if (c1[i] == c2[j])
        j++;
      if (j == len2)
        return i - len2 + 1;
    }
    return -1;
  }

动态规划

与分治法相似，在求解子问题的时候，保留子问题的解，后面子问题求解时可以直接拿来计算

对于一个规模为n的问题，将其分解为k个规模较小的子问题（阶段），按顺序求解子问题，前一子问题的解，为后一子问题的求解提供了有用的信息。在求解任一子问题时，通过决策求得局部最优解，依次解决各子问题。最后可以通过简单的判断，得到原问题的解。

阶段：求解第n个子问题称为第n个阶段。动态规划是按照顺序去求解子问题的，这里子问题的求解顺序很重要。

状态：在求解第n个阶段时，已求解n-1个阶段的解，称为状态。

决策：在求解第n个阶段时，根据状态和计算规则，可以得到第n个阶段时解。

特征

  1. 大问题可分解
  2. 子问题易解决

  3. 解可合并

    利用该问题分解出的子问题的解可以合并为该问题的解

  4. 子问题重叠

    计算某个子问题的解，并且保存，节省后面重复计算的时间

  5. 当前状态=上一状态+当前局部最优解

基本步骤

  1. 设计状态
  2. 状态转移方程
  3. 设定初始状态
  4. 状态转移
  5. 得解

  6. 分治法

    对于一个规模为n的问题，若该问题可以容易地解决（比如说规模n较小）则直接解决，否则将其分解为k个规模较小的子问题，这些子问题互相独立且与原问题形式相同，递归地解这些子问题，然后将各子问题的解合并得到原问题的解。分治法其实就是把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。

    基本特征

    1. 大问题可分解

      是使用分治法的前提，问题可分解，即是类似于数学归纳法，我们可以递归求解方程公式，然后根据方程公式设计出程序

    2. 子问题易解决

    3. 解可合并
    4. 子问题独立性

  7. 拓扑排序

    对一个有向无环图进行拓扑排序，是将其中所有的顶点排成一个线性序列，使得图中任意一对顶点u和v，若边∈E(G)，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。

    理解

    • 在一个有向图中，对所有节点进行排序，要求没有一个节点指向它前面的节点
    • 先统计所有节点的入度，对于入度为0的节点就可以分离出来，然后把这个节点指向的节点的入度减一。
    • 一直做改操作，直到所有的节点都被分离出来。

    • 如果最后不存在入度为0的节点，但还存在节点，那就说明有环，不存在拓扑排序，也就是很多题目的无解的情况。

      https://img-blog.csdn.net/20150507001759702

      实现思路

    • 先把入度为0的节点找到并且打印出来

    • 删除入度为0的节点，继续循环上一步，直到图为null

      算法具体思路

    1. 是遍历整个图中的顶点，找出入度为0的顶点，然后标记删除该顶点，更新相关顶点的入度，由于图中有V个顶点，每次找出入度为0的顶点后会更新相关顶点的入度，因此下一次又要重新扫描图中所有的顶点。故时间复杂度为O(V^2)

      问题：由于删除入度为0的顶点时，只会更新与它邻接的顶点的入度，即只会影响与之邻接的顶点。但是上面的方式却遍历了图中所有的顶点的入度。

    2. 先将入度为0的顶点放在栈或者队列中。当队列不空时，删除一个顶点v，然后更新与顶点v邻接的顶点的入度。只要有一个顶点的入度降为0，则将之入队列。此时，拓扑排序就是顶点出队的顺序。该算法的时间复杂度为O（V+E）

      实现

    3. 遍历图中所有的顶点，将入度为0的顶点 入队列。

    4. 从队列中出一个顶点，打印顶点，更新该顶点的邻接点的入度(减1)，如果邻接点的入度减1之后变成了0，则将该邻接点入队列。

    5. 一直执行上面 第二步，直到队列为空。

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      24
      25
      26
      27
      28
      29
      30
      31
      // leetcode 课程表问题 拓扑排序
      bool canFinish(const int &numCourses, const vector<vector<int>> &prerequisites)
        {
          vector<int> inDegree(numCourses, 0);
          unordered_map<int, vector<int>> mp;
          int n = prerequisites.size();
          for (int i = 0; i < n; i++)
          {
            mp[prerequisites[i][1]].emplace_back(prerequisites[i][0]);
            inDegree[prerequisites[i][0]]++;
          }
          for (int i = 0; i < numCourses; i++)
          {
            for (int j = 0; j < numCourses; j++)
            {
              if (inDegree[j] == 0)
              {
                for (auto &a : mp[i])
                  inDegree[a]--;
                inDegree[i]--;
              }
            }
          }
          for (int i = 0; i < numCourses; i++)
          {
            if (inDegree[i] > 0)
              return false;
          }
          return true;
        }
      };

深度优先 DFS

主要思路就是沿着一条路走到底，深入到不能深入为止，然后返回上一层继续深度优先，直到这条支路上没有可以探索的分支为止，就返回到上一层，相当于是暴力穷举

https://img-blog.csdnimg.cn/04aeba61d8b84e95b7986a6b225eb51d.png

特点

1、对每一个可能的分支路径深入到不能再深入为止，而且每个结点只能访问一次。要特别注意的是，二叉树的深度优先遍历比较特殊，可以细分为先序遍历、中序遍历、后序遍历（我们前面使用的是先序遍历）。
2、不全部保留结点，占用空间少；有回溯操作(即有入栈、出栈操作)，运行速度慢。
3、一般无回溯操作，即入栈和出栈的操作，所以运行速度比深度优先搜索要快些

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class TreeNode{
public:
  int val;
  TreeNode *left;
  TreeNode *right;

  TreeNode(): val(0), left(nullptr), right(nullptr){}
  TreeNode(int value): val(value), left(nullptr), right(nullptr){}
  TreeNode(int value, TreeNode* left, TreeNode* right): val(value), left(left), right(right){}
}

void func(int val){
  std::cout << "val = " << val << std::endl;
}

// 前序遍历
void DFSF(TreeNode *root){
  if(!root)return;
  func(root->val);
  DFS(root->left);
  DFS(root->right);
}

// 中序遍历
void DFSM(TreeNode *root){
  if(!root)return;
  DFS(root->left);
  func(root->val);
  DFS(root->right);
}

// 后序遍历
void DFSB(TreeNode *root){
  if(!root)return;
  DFS(root->left);
  DFS(root->right);
  func(root->val);
}

  1. 广度优先 BFS

    广度优先遍历是首先把起点相邻的几个点探索完成，然后去探索距离起点稍远一些（隔一层）的点，然后再去玩探索距离起点更远一些（隔两层）的点… 是一层一层的向外探索。

    遍历规则：
    1）先访问完当前顶点的所有邻接点。(应该看得出广度的意思)
    2）先访问顶点的邻接点先于后访问顶点的邻接点被访问。

    https://img-blog.csdnimg.cn/1073d7220e174309b87218d24e080e5d.png

    特点

    1、又叫层次遍历，从上往下对每一层依次访问，在每一层中，从左往右（也可以从右往左）访问结点，访问完一层就进入下一层，直到没有结点可以访问为止
    2、保留全部结点，占用空间大； 无回溯操作(即无入栈、出栈操作)，运行速度快。
    3、一般需存储产生的所有结点，占用的存储空间要比深度优先搜索大得多，因此，程序设计中，必须考虑溢出和节省内存空间的问题

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    class TreeNode{
    public:
      int val;
      TreeNode *left;
      TreeNode *right;

      TreeNode(): val(0), left(nullptr), right(nullptr){}
      TreeNode(int value): val(value), left(nullptr), right(nullptr){}
      TreeNode(int value, TreeNode* left, TreeNode* right): val(value), left(left), right(right){}
    }

    void func(int val){
      std::cout << "val = " << val << std::endl;
    }

    void BFS(TreeNode *root){
      std::queue<TreeNode* > bfs;
      func(root->val);
      while(!bfs.empty()){
        TreeNode *p = bfs.front();
        bfs.pop();
        if(!p)continue;
        func(p->val);
        bfs.push(p->left);
        bfs.push(p->right);
      }
    }

双指针

对撞指针

指针一左一右向中间逼近，例如二分查找法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int func(vector<int> nums, int target)
{
 int l = 0;
 int r = nums.size() - 1;
 sort(nums.begin(), nums.end());
 while (r > l) {
  int mid = (l + r) / 2;
  if (nums[mid] < target)
   l = mid + 1;
  else
   r = mid;
 }
 return nums[r] == target ? r : -1;
}

快慢指针

一快一慢，步长一大一小，环的问题和单链表寻找中间节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Node
{
public:
 Node* next;
 int   val;
};

// 判断是否有环
bool func(Node* node)
{
 Node* fast = node->next;
 Node* low  = node;
 while (fast != low) {
  if (!fast->next->next)
   return false;  // 无环
  fast = fast->next->next;
  low  = low->next;
 }
 return true;
}

// 寻找中间节点
Node* func(Node* node)
{
 Node* fast = node;
 Node* low  = node;
 while (fast->next) {
  if (!fast->next->next)
   break;
  fast = fast->next->next;
  low  = low->next;
 }
 return low;
}
Node* func(Node* head){
 Node* fast = head;
 Node* slow = head;
 while(fast){
  if(fast->next) fast = fast->next->next;
  else break;
  slow = slow->next;
 }
 return slow;
}

滑动窗口

一般是右端向右扩充，达到停止条件之后不动，左端向右端逼近，达到停止条件之后不动，右端继续运动

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// leetcode 3th
int func(string s)
{
 int     left  = 0;
 int     right = 0;
 int     n   = s.length();
 unordered_set<char> set;
 int     res = 0;

 for (; right < n; ++right) {
  if (set.find(s[right]) == set.end())
   set.insert(s[right]);
  else {
   res = max(res, right - left);
   while (set.find(s[right]) != set.end()) {
    set.erase(s[left]);
    left++;
   }
   set.insert(s[right]);
  }
 }
 return max(res, right - left);
}

排序

快速排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
enum{LEFT, RIGHT};

void quicksort(std::vector<int>& vec, const int& begin, const int& end){
  if(begin >= end)return;
  int flag = LEFT;
  int left = begin;
  int right = end;
  while(left < right){
    if(flag == LEFT){
      while(vec[left] < vec[right])right--;
      flag == RIGHT;
    }
    else{
      while(vec[left] < vec[right])left--;
      flag == LEFT;
    }
    int temp = vec[left];
    vec[left] = vec[right];
    vec[right] = temp;
  }
  quicksort(vec, begin, left - 1);
  quicksort(vec, left + 1, end);
}

时间复杂度 $O(nlog_2n)$

冒泡排序

1
2
3
4
5
6
7
8
9
10
void slowsort(std::vector<int>& vec){
  int n = vec.size();
  for(int i = 0; i < n; i++)
    for(int j = 0; j < n; j++)
      if(vec[i] < vec[j]){
        int temp = vec[i];
        vec[i] = vec[j];
        vec[j] = temp;
      }
}

时间复杂度 $O(n^2)$

多次运行结果验证，90%的概率是快速排序速度快于冒泡排序

归并排序

堆排序

桶排序

位运算

可以使用位运算来判断两个字符串是否有相同的字符

1
2
3
4
5
6
7
8
bool compare(const string& s1, const string s2) {
  vector<int> mask(2, 0);
  for(const char &c : s1)
    mask[0] |= 1 << (c - 'a');
  for(const char &c : s2)
    mask[1] |= 1 << (c - 'a');
  return mask[0] & mask[1];
}

Brian Kernighan算法：Brian Kernighan算法可以用于清除二进制数中最右侧的1。Brian Kernighan算法的做法是先将当前数减一，然后在与当前数进行按位与运算。

可以统计一个数字中二进制中1的数目，即1比特数

1
2
3
4
5
int n = 0;
while(x) {
 x = x & (x - 1);
 n++;
}

线段树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
template<typename T>
class line_segment_tree {
private:
  vector<T> tree;
  int n;
 // 建树
  void build(int node, int begin, int end, const vector<T>& nums) {
    if(begin == end) {
      tree[node] = nums[begin];
      return;
    }
    int mid = (begin + end) >> 1;
    build((node >> 1) + 1, begin, mid, nums);
    build((node >> 1) + 2, mid + 1, end, nums);
    tree[node] = tree[(node >> 1) + 1] + tree[(node >> 1) + 2];
  }
 // 改变某个位置的数据
  void change(int index, int val, int node, int begin, int end) {
    if(begin == end) {
      tree[node] = val;
      return;
    }
    int mid = (begin + end) >> 1;
    if(index <= mid) 
      change(index, val, (node << 1) + 1, begin, mid);
    else 
      change(index, val, (node << 1) + 2, mid + 1, end);
    tree[node] = tree[(node >> 1) + 1] + tree[(node >> 1) + 2];
  }
 // 输出某个范围内的和
  int range(int left, int right, int node, int begin, int end) {
    if (left == begin && right == end) {
      return tree[node];
    }
    int mid = (begin + end) >> 1;
    if (right <= mid) {
      return range(left, right, (node << 1) + 1, begin, mid);
    } else if (left > mid) {
      return range(left, right, (node << 1) + 2, mid + 1, end);
    } else {
      return range(left, mid, (node << 1) + 1, begin, mid) + range(mid + 1, right, (node << 1) + 2, mid + 1, end);
    }
  }

public:
 // 初始化，存储一个数组
  line_segment_tree(const vector<T>& nums) : n(nums.size()), tree(vector<T>(nums.size() * 4)) {
    build(0, 0, n - 1, nums);
  }
};

寻找质数的算法

埃氏筛

1
2
3
4
5
6
7
8
9
10
11
12
13
int countPrimes(int n) {
  int      ans = 0;
  vector<bool> vs(n, true);
  for (int i = 2; i < n; ++i) {
   if (vs[i]) {
    ans++;
    if ((long long) i * i < n)
     for (int j = i * i; j < n; j += i)
      vs[j] = false;
   }
  }
  return ans;
 }

线性筛

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void countPrimes(int n) {
 vector<int>  primes;
 vector<bool> isprime(n, true);
 for (int i = 2; i < n; ++i) {
  if (isprime[i])
   primes.emplace_back(i);
  int primenum = primes.size();
  for (int j = 0; j < primenum && i * primes[j] < n; ++j) {
   isprime[i * primes[j]] = 0;
   if (i % primes[j] == 0)
    break;
  }
 }
}

N数和

leetcode-216

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
 public:
 vector<vector<int>> ans;
 vector<int>     temp;
 vector<vector<int>> combinationSum3(int k, int n) {
  for (int i = 1; i < (1 << 9); i++) {
   if (check(i, k, n)) {
    ans.emplace_back(temp);
   }
  }
  return ans;
 }
 bool check(int mask, int k, int n) {
  temp.clear();
  int sum = 0;
  for (int i = 1; i <= 9; i++) {
   if ((1 << i) & mask) {
    temp.emplace_back(i);
    sum += i;
   }
  }
  return temp.size() == k && sum == n;
 }
};

前缀和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 一维前缀和
void Prefix_Sum(const vector<int>& grid) {
 int     n = grid.size();
 vector<int> sum(n, 0);
 sum[0] = grid[0];
 for (int i = 1; i < n; i++) {
  sum[i] = sum[i - 1] + grid[i];
 }
}

// 二维前缀和
void Prefix_Sum(const vector<vector<int>>& grid) {
 int         m = grid.size();
 int         n = grid.at(0).size();
 // 使用 m + 1 和 n + 1 主要是就不需要计算0处的数据了，初始化全为0就可以了
 vector<vector<int>> sum(m + 1, vector<int>(n + 1, 0));
 for (int i = 1; i < n + 1; ++i) {
  for (int j = 1; j < n + 1; ++j) {
   sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + grid[i - 1][j - 1];
  }
 }
}