QP二次规划

一些定义

对于一个函数 $F:R^n→R^m$ 是一个将欧式 n 维空间的函数，该函数由 m 个实函数构成， $y_1(x_1,…,x_n),…,y_m(x_1,…,x_n)$

Jacobian 矩阵

函数 F 的偏导数组成一个 m 行 n 列的矩阵，就是 Jacobian 矩阵

$$J_F(x_1,...,x_n)=\begin{bmatrix}\frac{\partial y_1}{\partial x_1}&...&\frac{\partial y_1}{\partial x_n}\\...&...&...\\\frac{\partial y_m}{\partial x_1}&...&\frac{\partial y_m}{\partial x_n}\end{bmatrix}$$

也可以表示为 $\frac{\partial(y_1,…,y_m)}{\partial (x_1,…,x_n)}$。如果对于一个 $p\in R^n$ ，函数 F 在 p 点可微，则 F 在这一点的导数由 $J_F(p)$ 给出

Hessian 矩阵

如果 F 的所有二阶导数都存在，则 F 的 Hessian 矩阵为

$$H_F(x_1,...,x_n)=\begin{bmatrix}\frac{\partial^2 F}{\partial x_1^2}&...&\frac{\partial^2 F}{\partial x_1\partial x_n}\\...&...&...\\\frac{\partial^2 F}{\partial x_n\partial x_1}&...&\frac{\partial^2 F}{\partial x_n^2}\end{bmatrix}$$

可以利用二阶导数的值判断梯度下降的速度

二次规划 QP

二次规划(QP, Quadratic Programming)定义：目标函数为二次函数，约束条件为线性约束，属于最简单的一种非线性规划。说白了就是一种对于控制理论的一种优化，约束条件和线性规划问题的约束条件一样，都是线性等式或线性不等式。即

$$\left\{\begin{aligned}&min\frac{1}{2}x^TGx+H^Tx&&\\&a_i^Tx\leq b_i&&i\in I=\{1...m\}\\&a_i^Tx=b_i&&i\in \varepsilon = \{m+1,...m+l\}\end{aligned}\right.$$

其中 $\varepsilon$ 表示等式约束的指标集， $I$ 表示不等式约束的指标集

一般二次规划问题可以分成以下几类

• 凸二次规划问题：G半正定，问题有全局解
• 严格凸二次规划问题：G正定，问题有唯一全局解
• 一般二次规划问题：G不定，问题有稳定点或局部解

Language 乘数法

求函数 $f(x,y)$ 在条件 $\phi (x,y)=0$ 约束下的可能极值点，构造 language 函数，即

$$L(x,y,\lambda)=f(x,y)+\lambda \phi(x.y)$$

求偏导得

$$L_x=f_x+\lambda \phi_x\\L_y=f_y+\lambda \phi_y\\L_\lambda = \phi$$

令上式均为 0 可以解出 $x,y,\lambda$ 的值，其中的 $x,y$ 就是可能的极值点的坐标。对于多个约束条件可以引入多个 $\lambda$ ，求解与上述一致

KKT 条件

1. KKT 条件核心思想

   对于一个不等式约束的方程

   最小化问题

   $$\min f(x)\\g(x)\leq 0$$

   最大化问题

   $$\max f(x)\\g(x)\geq 0$$

   首先先不考虑约束 $g(x)$，直接对 $f(x)$ 求导，最终能得到一个最优值 $x^\star $，接下来把最优值带入到约束中，会有三种情况

   • 满足 $g(x)$ 约束但是 $g(x)\not =0$

     正好满足约束，最优解为 $x^\star $，但是实际上这个约束并没有起作用，问题实际上转化为无约束优化问题，但是同样的构造 Language 函数

     $$L(x,\lambda)=f(x)+\lambda g(x)$$

     由于此时约束无用，也就可以把 $\lambda=0$，最终实际上是把约束条件给转为 0，也就没有约束

   • $g(x)=0$

     最优解 $x^\star $ 使得约束为等号，正好在约束的边界上，此时就是 Language 乘数法所能解决的，构造函数

     $$L(x,\lambda)=f(x)+\lambda g(x)$$

   • 不满足 $g(x)$ 的约束

     显然此时不满足约束，结果被舍弃，最终的结果一定在满足约束条件的范围内

     最终满足条件的两种情况中的 Language 方程可以统一为 $\lambda g(x^\star )=0$，这就是 KKT 条件的精髓

2. 公式

   首先给出一个仅含有不等式约束

   $$\left\{\begin{aligned}\min f(x)\\g(x)\leq 0\end{aligned}\right.\Rightarrow KKT\left\{\begin{aligned}&\triangledown f(x^\star )+\lambda \triangledown g(x^\star )=0\\&\lambda g(x^\star )=0\\&\lambda\geq 0\\&g(x^\star )\leq 0 \end{aligned}\right.$$

   依旧需要引入 Language 函数

   $$L(x,\lambda)=f(x)+\lambda g(x)$$

   对于上述 KKT 条件中

   • 1式：对拉格朗日函数求梯度(若X一维就是求导)，其中，下三角表示梯度
   • 2式：核心公式 $\lambda=0$ 或 $g(x^\star )=0$，但是此处要求不能同时为 0
   • 3式：Language 乘子 $\lambda$ 必须是正的

   • 4式：原约束

     上述中 1，2式可以求出最优的 $x^\star ,\lambda^\star $，但是由于 2 式需要两种情况，所以存在多个最优解，而3，4 式主要是验证先前的结果是否满足条件。一般问题的解析分为两种情况

   • $\lambda=0$ 计算 $x^\star $ 并且验证 4式条件

   • $\lambda\not=0$ 计算 $x^\star ,\lambda^\star $，并且验证3，4式条件

     将不等式与等式条件推广，可以得到多个约束的公式

     $$\min f(x)\\g_i(x)\leq 0,i\in[1,m]\Rightarrow m 个不等式约束\\h_j(x)=0,j\in[1,n]\Rightarrow n个等式约束$$

     对应的 Language 函数为

     $$L(x,\{\lambda_i\},\{\mu_j\})=f(x)+\sum_{i=1}^m\lambda_ig_i(x)+\sum_{j=1}^n\mu_jh_j(x)$$

     其中的参数 $\{\lambda_i\},\{\mu_j\}$ 表示多个约束

     对应的 KKT 条件为

     $$\left\{\begin{aligned}&\triangledown f(x^\star )+\sum_{i=1}^m\lambda_i \triangledown g_i(x^\star )+\sum_{j=1}^n\mu_j\triangledown h_j(x^\star )=0\\&\lambda_i g_i(x^\star )=0,i\in[1,m]\\&\lambda_i\geq 0,i\in[1,m]\\&g(x^\star )\leq 0,i\in[1,m]\\&h_j(x^\star )=0,j\in [1,n] \end{aligned}\right.$$

     这个实质上是几个不等式与等式约束，与之前的解法一致，利用等式求解，用不等式验证。由于上述公式中有 m 个 Language 乘子，每个都有两种情况，所以就是 $2^m$ 种。但是能解出最优解的一定是等式，而不等式是排除解的方法。

3. 充分性必要性说明

   KKT 条件是判断某点是极值点的必要条件，不是充分条件。KKT 的解不一定是最优解，但是最优解一定满足 KKT 条件。

   对于 凸规划，KKT 条件是充要条件，只要满足 KKT 条件，则一定极值点，并且得到的一定是全局最优解。

   凸规划是指目标函数为凸函数，不等式约束函数也为凸函数，等式约束函数是仿射的（理解为线性的也可以）。对于凹函数实际上就是凸函数加负号，本质是一样的。

4. Min/Max与 $\leq 0/\geq 0$ 的规定

   也就是

   • 如果目标为最小化Min问题，那么不等式约束就要整理为 $\leq 0$ 形式

   • 如果目标为最小化Max问题，那么不等式约束就要整理为 $\geq 0$ 形式

     

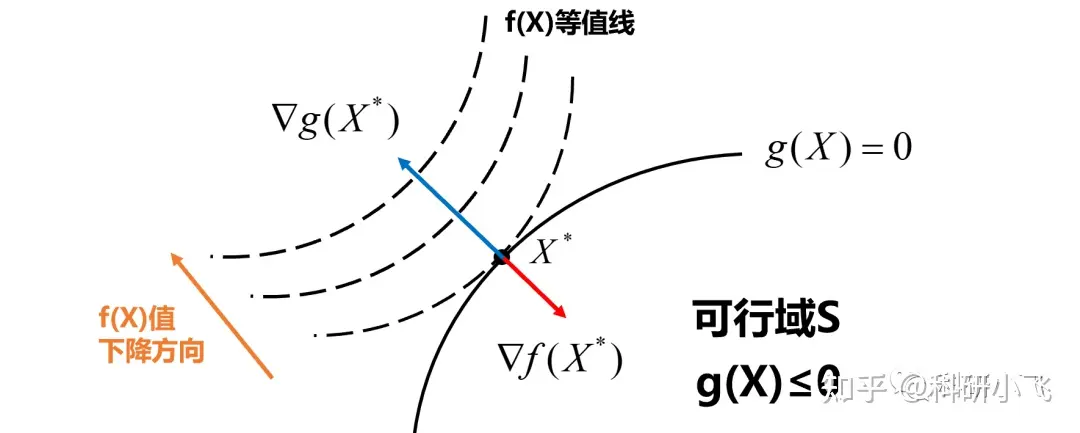
     由于梯度指的是函数下降的方向，所以垂直于等值线。如图在最优解点， $f(x^\star )$ 和 $g(x^\star )$ 梯度方向共线方向相反，这在数学上写法是

     $$-\triangledown f(x^\star )=\lambda \triangledown g(x^\star )\\\Downarrow\\\triangledown f(x^\star )+\lambda \triangledown g(x^\star )=0$$

     这实际上就是 KKT 条件的第一个等式，而且由于 $g(x)$ 的梯度方向与 $f(x)$ 负梯度方向相同，这就是KKT条件中的一个条件 $\lambda ≥ 0$

     但是如果对于最大化问题，约束为 $g(x)\leq 0$，此时 $g(x^\star )$ 梯度方向与 $f(x^\star )$ 方向相同，所以上述公式就变为 两项做差 或者 $\lambda<0$，实际上结果是没有变化的。

     对于两个约束来说

     

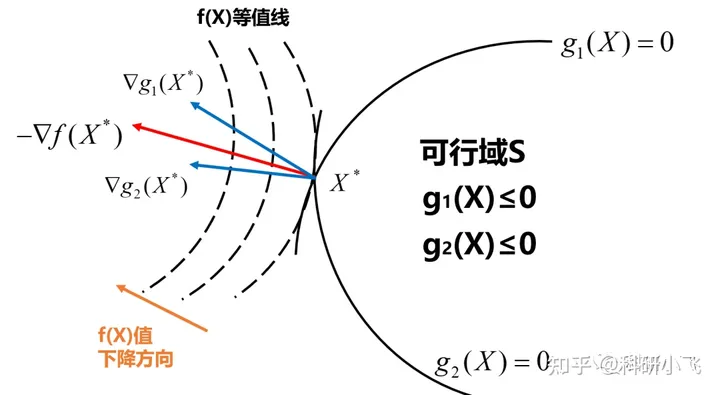
     那就可以表示为向量相加的结果

     $$-\triangledown f(x^\star )=\lambda_1\triangledown g_1(x^\star )+\lambda_2 \triangledown g_2(x^\star )\\\Downarrow \\\triangledown f(x^\star )+\lambda_1\triangledown g_1(x^\star )+\lambda_2 \triangledown g_2(x^\star )=0$$

     这也是 KKT 条件的第一个等式

5. 正则性条件/约束规范说明

   KKT 条件对于目标函数和约束函数也是有要求的，目标函数和约束函数均可为连续可微函数。

   正则性条件/约束规范：以下方程组是线性独立的

   $$\triangledown g_i(x^\star ):i\in I(x^\star )\cup \triangledown h_j(x^\star ):j\in[1,n]$$

   其中 $I(x^\star )$ 指的是起作用约束的集合

下面的KKT，以后再来探索吧

KKT条件，原来如此简单 | 理论+算例实践 - 知乎 (zhihu.com)

最优化（3）KKT条件为什么用不了了_哔哩哔哩_bilibili

QP——等式约束

一般形式

$$\left\{\begin{aligned}min\ \frac{1}{2}x^TGx+h^Tx\\A^Tx=b\end{aligned}\right.$$

其中 $b\in R^m,A\in R^{n\times m},rank(A)=m, n>m$

其中 $G$ 是由二阶导构成的 hessian 矩阵

求解方法

变量消去法

步骤

1. 将 $x$ 分成基本变量 $x_B$与非基本变量 $x_N$ 两部分，利用等式约束将基本变量用非基本变量表示出来
2. 再将基本变量带入目标函数，从而消去基本变量，把问题化为一个关于非基本变量的无约束最优化问题
3. 最后求解无约束最优化问题的方法解之

具体步骤

将 A 分块，使其包含一个 $m \times m$ 非奇异矩阵 $A_B,x,h$ 做对应的分块

$$x=\begin{bmatrix}x_B\\x_N\end{bmatrix},A=\begin{bmatrix}A_B\\A_N\end{bmatrix},G=\begin{bmatrix}G_{BB}&&G_{BN}\\G_{NB}&&G_{NN}\end{bmatrix},h=\begin{bmatrix}h_B\\h_N\end{bmatrix}$$

所以等式约束 $A^Tx=b$ 转化为

$$\begin{bmatrix}A_B\\A_N\end{bmatrix}^T\begin{bmatrix}x_B\\x_N\end{bmatrix}=b \rightarrow A_Bx_B+A_Nx_N=b$$

更换以下变量位置

$$x_B=A_B^{-1}b-A_B^{-1}A_Nx_N$$

则

$$x=\begin{bmatrix}x_B\\x_N\end{bmatrix}=\begin{bmatrix}A_B^{-1}b-A_B^{-1}A_Nx_N\\x_N\end{bmatrix}=\begin{bmatrix}A_B^{-1}\\0\end{bmatrix}+\begin{bmatrix}-A_B^{-1}A_N\\I\end{bmatrix}x_N=x_0+Zx_N$$

转变为一个 $x=x_0+Zx_N$ 的形式，将其带入目标函数，消去基本变量，问题变为一个关于非基本变量的无约束最优化问题

将上式带入目标函数中

$$min\ f(x)=\frac{1}{2}x^TGx+h^Tx=\frac{1}{2}(x_0+Zx_N)^TG(x_0+Zx_N)+h^T(x_0+Zx_N)$$

其中除了 $x_N$ 其他都是已知的常数项，由于常数项不影响优化结果，所以优化过程中省略常数项。另外找到所有的 $x_N^TPx_N$ 和 $Qx_N$ 的形式的项，可得如下形式：

$$\left\{\begin{aligned}min\ f(x)&=\frac{1}{2}x_N^TPx_N+\frac{1}{2}Z^Tx_N^TGx_0+\frac{1}{2}x_0^TGZx_N+\frac{1}{2}x_0^TGx_0+Qx_N\\P&=Z^TGZ\\Q&=x_0^TGZ+h^TZ\end{aligned}\right.$$

求最值实际上求 $\dot{f(x)}=0$ 即可，即

$$\dot{f(x)} = \frac{1}{2}Z^T(G+G^T)Zx_N+\frac{1}{2}Z^T(G+G^T)x_0+Q^T=0$$

如果想要有唯一最优解，必须满足 $Z^T(G+G^T)Z$ 正定

Language 法

步骤

等式约束的二次规划的 Lagrange 函数为

$$L(x,\lambda)=\frac{1}{2}x^TGx+h^Tx+\lambda (A^Tx-b)$$

其中 $\lambda$ 称为 Lagrange 乘数，正负都有可能。Lagrange乘数法将原本的约束优化问题转换成等价的无约束优化问题，即

$$\underset{x,\lambda}{min} \ L(x,\lambda)$$

计算 $L$ 对 $x$ 和 $\lambda$ 的偏导，并且设为零，可得最优解的必要条件

$$\left\{\begin{aligned}\frac{\partial L}{\partial x}&=Gx+h+\lambda =0 && 定常方程式\\\frac{\partial L}{\partial \lambda}&=A^Tx-b=0&&约束条件\end{aligned}\right.$$

表示为方程组

$$\begin{bmatrix}G&&A\\A^T&&0\end{bmatrix}\begin{bmatrix}x\\\lambda\end{bmatrix}=\begin{bmatrix}-h\\b\end{bmatrix}$$

求解之后得到最优解

方法对比

变量消去法其实是转化成了一个 n - m 维的问题，也就是说求解 n − m 个方程组就能解决这个问题。而 Lagrange法是将其转化成一个 n + m 维的问题，即 n 个变量， m 个乘子。所以可见，如果模型维度太大，建议使用变量消去法，很直观，使用非基数来表示基变量，但是由于需要计算 $A_B^{-1}$ ，当 $A_B$ 接近奇异时会导致误差很大

QP——不等式约束

一个标准的等式不等式联合约束 QP 原模型

$$\min \frac{1}{2}x^THx+g^Tx\\a_i^Tx=b_i,i\in E\\h_j^Tx\leq t_j,j\in I$$

$i\in E$ 表示的是 m 个等式约束集合， $i\in I$ 表示的是 n 个不等式约束集合。对于不等式约束下的 QP 问题有多种求解方法

并且由

$$f(x)=\frac{1}{2}x^THx+g^Tx\\g_i(x)=ax_i-b_i\\h_i(x)=h_i^Tu-t_i$$

求解方法

Lagrange乘数法与KKT条件

一般形式

$$\left\{\begin{aligned}min\ \dot{f(x)}\\g(x)\leq 0\end{aligned}\right.$$

其中约束不等式 $g(x)\leq 0$ 称为原始可行性，可以定义可行域

$$K=\{x\in R^n|g(x)\leq0\}$$

假设 $x^\star $ 为满足约束条件的最佳解，分两种情况讨论

• $g(x^\star )<0$ 最佳解位于 K 的内部，称为内部解(interior solution)，这时约束条件是无效的 (inactive)

  必要条件

  约束条件无效的情况下， $g(x)$ 不起作用，约束优化问题退化为无约束优化问题， 因此驻点 $x^\star $ 满足 $\nabla f=0且\lambda=0$

• $g(x^\star )=0$ 最佳解位于 K 的边界，称为边界解(boundarysolution)，这时约束条件是有效的 (active)

  必要条件

  在约束条件有效的情形下，约束不等式变成等式 $g(x)=0$，这与前述 Lagrange 乘数法的情况相同，可以证明驻点 $x^\star $ 发生于 $\nabla f\in span \nabla g$，其中 span 是生成子空间。即 $\exist \lambda\rightarrow \nabla f=-\lambda \nabla g$，并且这里的正负号有意义。因此我们希望最小化 $f$，梯度 $\nabla f$ （函数 $f$ 在点 x 的最陡上升方向），应该指向可行域 K 的内部，因为最优解是在边界取到的，但同时 $\nabla g$ 指向 K 的外部（ $g(x)>0$ ）的区域，因为约束是 $g(x)\leq 0$，因此 $\lambda \geq 0$ ，称为对偶可行性

因此，不论是内部解或者边界解， $\lambda g(x)=0$ 恒成立，称为互补松弛性。综合上述两种情况，最佳解的必要条件包括 Lagrange 函数 $L(x,\lambda)$ 的定常方程式，原始可行性，对偶可行性，互补松弛性

$$\left\{\begin{aligned}&\nabla_x L=\nabla f+\lambda \nabla g=0\\&g(x)\leq 0\\&\lambda\geq 0\\&\lambda g(x) =0\end{aligned}\right.$$

这些条件合称为Karush-Kuhn-Tucker (KKT)条件。如果我们要最大化 $f(x)$ 且受限于 $g(x)\leq0$，那么对偶可行性要改成 $\lambda \leq 0$

标准约束优化

考虑标准优化问题，即非线性规则

$$\left\{\begin{aligned}&min\ f(x)\\&g_j(x)=0&&j=1…m\\&h_k(x)\leq 0&&k=1…p\end{aligned}\right.$$

定义 Lagrange 函数

$$L(x,\{\lambda_j\},\{u_k\})=f(x)+\sum_{j=1}^m{\lambda_j g_j(x)}+\sum_{k=1}^pu_kh_k(x)$$

其中 $\lambda_j$ 是对应 $g_j(x)=0$ 的 Lagrange 乘数， $u_k$ 是对应 $h_k(x)\leq 0$ 的 Lagrange 乘数，或称为 KKT乘数。KKT条件包括定常方程式，原始可行性，对偶可行性，互补松弛性

$$\left\{\begin{aligned}&\nabla_x L=0\\&g(x)= 0&&j=1...m\\&h_k(x)\leq0\\&u_k\geq 0\\&u_kh_k(x)=0&&k=1...p\end{aligned}\right.$$

栗子

1. 对于这个问题

   $$\left\{\begin{aligned}min\ x_1^2+x_2^2\\x_1+x_2=1\\x_2\leq \alpha\end{aligned}\right.$$

   其中 $(x_1,x_2)\in R^2$ ， $\alpha$ 为实数，写出 Lagrange 函数

   $L(x_1,x_2,\lambda,\mu)=x_1^2+x_2^2+\lambda (1-x_1-x_2)+\mu (x_2-\alpha)$

   KKT 方程组

   $$\left\{\begin{aligned}&\frac{\partial L}{\partial x_i}=0&&i=1,2\\&x_1+x_2=1\\&x_2-\alpha\leq0\\&u\geq 0\\&u(x_2-\alpha)=0\end{aligned}\right.$$

   求偏导为

   $$\left\{\begin{aligned}\frac{\partial L}{\partial x_1}&=2x_1-\lambda = 0\\\frac{\partial L}{\partial x_2}&=2x_2-\lambda + \mu=0\end{aligned}\right.$$

   解得

   $$\left\{\begin{aligned}x_1&=\frac{\lambda}{2}\\x_2&=\frac{\lambda-\mu}{2}\end{aligned}\right.$$

   带入约束等式，得

   $$x_1+x_2=\lambda-\frac{\mu}{2}=1$$

   合并结果为

   $$\left\{\begin{aligned}x_1&=\frac{\mu}{4}+\frac{1}{2}\\x_2&=-\frac{\mu}{4}+\frac{1}{2}\end{aligned}\right.$$

   加入约束不等式

   $$-\frac{\mu}{4}+\frac{1}{2}\leq \alpha \Rightarrow \mu\geq 2-4\alpha$$

   分3种情况讨论

   • $\alpha > \frac{1}{2}$ 则对于 $u=0>2-4\alpha$ 满足所有的KKT条件，约束不等式无效， $x_1^\star =x_2^\star =\frac{1}{2}$ 是内部解，目标函数的极小值为 $\frac{1}{2}$
   • $\alpha = \frac{1}{2}$ 则 $u=0=2-4\alpha$ 满足所有的KKT条件， $x_1^\star =x_2^\star =\frac{1}{2}$ 是内部解，因为 $x_2^\star =\alpha$，即满足 $x_2^\star -\alpha=0$
   • $\alpha<\frac{1}{2}$ 这时约束不等式是有效的，$u=2-4\alpha>0$，则 $x_1^\star =1-\alpha$ 且 $x_2^\star =alpha$，目标函数的极小值为 $(1-\alpha)^2+\alpha^2$

2. 标准约束优化

   $$\left\{\begin{aligned}&min\ f(x)=-2x_1^2-x_1^2\\&x_1^2+x_2^2-x=0\\&-x_1+x_2\geq 0\\&x_1\geq 0,x_2\geq 0\end{aligned}\right.$$

   试验证 $x^\star =(1,1)^T$ 为KKT点，并求出问题的 KKT 对

   $$\left\{\begin{aligned}f(x)&=-2x_1^2-x_1^2\\g(x)&=x_1^2+x_2^2-2\\h_1(x)&=x_1-x_2\\h_2(x)&=-x_1\\h_3(x)&=-x_2\end{aligned}\right.$$

   求梯度，得到

   $$\nabla f(x)=\begin{bmatrix}-4x_1\\-2x_2\end{bmatrix},\nabla g(x)=\begin{bmatrix}2x_1\\2x_2\end{bmatrix}\\\nabla h_1(x)=\begin{bmatrix}1\\-1\end{bmatrix},\nabla h_2(x)=\begin{bmatrix}-1\\0\end{bmatrix},\nabla h_3(x)=\begin{bmatrix}0\\-1\end{bmatrix}$$

   把 $x^\star =(1,1)^T$ 带入以上的式子，由KKT条件得

   $$\left\{\begin{aligned}-4+2\lambda +\mu_1-\mu_2=0\\-2+2\lambda -\mu_1+\mu_3=0\end{aligned}\right.$$

   由于

   $$\left\{\begin{aligned}\mu_2h_2(x)=0\\\mu_3h_3(x)=0\end{aligned}\right.\rightarrow \left\{\begin{aligned}\mu_2^\star =0\\\mu_3^\star =0\end{aligned}\right. \Rightarrow \left\{\begin{aligned}-4+2\lambda +\mu_1=0\\-2+2\lambda -\mu_1=0\end{aligned}\right. \Rightarrow \left\{\begin{aligned}&\lambda^\star =1.5\\&\mu_1^\star =1\end{aligned}\right.$$

   这表明 $x^\star $ 是KKT点， $(x^\star ,(\lambda^\star ,\mu^\star ))$是KKT对，其中

   $$\left\{\begin{aligned}&\lambda^=1.5\\&\mu^\star =\begin{bmatrix}1&0 &0\end{bmatrix}^T\end{aligned}\right.$$

内点法

基本思想

将优化问题的可行域视为一个凸集，并通过一个内点序列来逐步接近最优解，而不是像单纯形法那样在顶点上进行搜索。在内点法中，每个内点表示一个可行解，而算法将不断迭代，使内点逐渐接近最优解。通过在内点附近构造一个特定的路径，内点法可以在有限的步数内找到最优解

步骤

$$\left\{\begin{aligned}&min\ f(x)\\&g_j(x)=0&&j=1…m\\&h_(x)\leq 0&&k=1…p\end{aligned}\right.$$

写出对应的 Lagrange 函数

$$L(x,\{\lambda_j\},\{u_k\})=f(x)+\sum_{j=1}^m{\lambda_j g_j(x)}+\sum_{k=1}^pu_kh_k(x)$$

对应的 KKT 条件为

$$\left\{\begin{aligned}&Gx+c-A^T_{\varepsilon}\lambda-A^T_{I}\mu=0\\&a_i^Tx\leq b_i&i\in I\\&a_i^Tx=b_i&i\in \varepsilon\\&\mu_i\geq0&i\in I\\&\mu_i(a_i^Tx-b_i)=0&i\in I\end{aligned}\right.$$

其中

$$\left\{\begin{aligned}A_{\varepsilon}=\{a_i^T\}_{i\in \varepsilon} \in R^{m_1\times n}\\A_I=\{a_i^T\}_{i \in I}\in R^{m_2\times n}\end{aligned}\right.$$

相当于把两组不同的约束做了拆分。

可以添加一组松弛变量

$$\left\{\begin{aligned}&Gx+c-A^T_{\varepsilon}\lambda-A^T_{I}\mu=0\\&A_{\varepsilon}-b_{\varepsilon}=0\\&A_Ix-b_I-y=0\\&(\mu,y)\geq0&i\in I\\&\mu_iy_i=0&i\in I\end{aligned}\right.$$

这里的 $b_{\varepsilon},b_I$ 和之前的意思类似，就是根据不同的指标集把b区分成不同的两个列向量

写成函数的形式

$$F(x,y,\lambda,\mu)=\begin{bmatrix}&Gx+c-A^T_{\varepsilon}\lambda-A^T_{I}\mu\\&A_{\varepsilon}-b_{\varepsilon}\\&A_Ix-b_I-y\\&U Y1\end{bmatrix}$$

其中 $U, Y\in R^{n_2\times n_2}$，最终的目的就是 $F(x,y,\lambda,\mu)=0$，再加上 $(\mu, y)\geq 0$ 就是完整的KKT条件了

可以适当添加一个松弛条件，即解方程

$$F(x,y,\lambda,\mu)=\begin{bmatrix}0\\0\\0\\\tau 1\end{bmatrix}$$

由于要求 $(\mu,y)>0$ ，所以不断缩小 $\tau \rightarrow 0$，就是最终的解

求解这个方程的解就需要求解 jacobi 矩阵

$$\begin{bmatrix}G&0&-A_{\varepsilon}^T&-A_I^T\\A_{\varepsilon}&0&0&0\\A_I&-I&0&0\\0&U&0&Y\end{bmatrix}\begin{bmatrix}\Delta x\\\Delta y\\\Delta \lambda\\\Delta\mu\end{bmatrix}=\begin{bmatrix}-r^d\\-r^p\\-r^y\\-UY1+\sigma \beta 1\end{bmatrix}$$

其中

$$\left\{\begin{aligned}&\beta=\frac{y^T\lambda}{m_2}\\&\sigma \in(0,1)作为一个系数\\&r^d=Gx+c-A^T_{\varepsilon}\lambda-A^T_{I}\mu\\&r^p=A_{\varepsilon}-b_{\varepsilon}\\&r^y=A_Ix-b_I-y\end{aligned}\right.$$

积极集法

积极集法就是一堆active的约束条件的集合。active的定义是：给定任意一个在可行域内的点x，即可行解，在x下，不等式约束条件取到等号。即在 $x=x^\star $ 这个可行解下 $g(x)\geq0⇒g(x^\star )=0$

active set 里面包括了所有的等式约束以及一些可以取到等号的不等式约束

方法核心思想：如果我们知道最优点处的active的约束，就可以把那些inactive的约束条件都剔除掉，将带不等式约束的二次规划问题转变为等式约束的二次规划问题，降低搜索解的复杂度。但其有一个前提，给定的迭代的起始点要是一个可行解。

算法流程

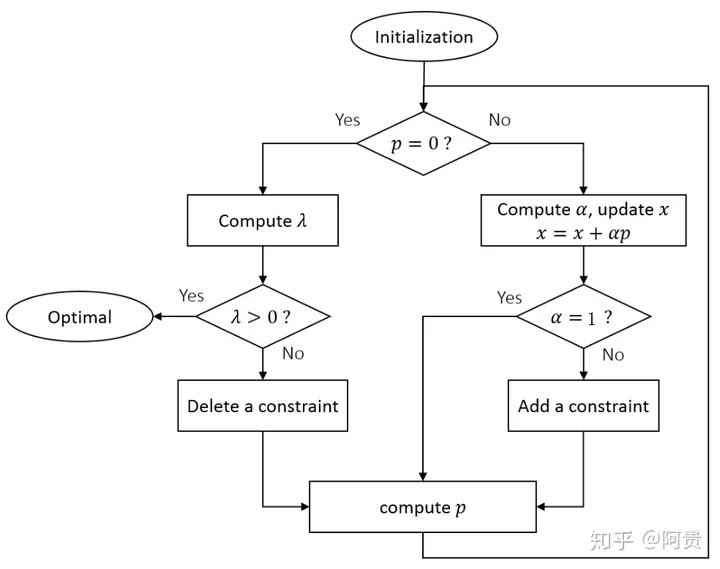
图中的p是一个当前迭代点的改进方向，每次迭代，我们把从约束条件集合中拿出来的约束条件假设为active约束条件进行尝试，加入的集合称为工作集，这个集合是随着迭代不断变化的。如果第k次的迭代点 $x_k$ 不是当前工作集下的最优点，就通过求解当前工作集下的active约束的QP问题来得到一个最优解x，工作集也有可能为空，即求解原QP问题在无约束条件下的最优解，方向 $p=x^\star -x_k$， $x_k$ 朝着p移动可以使得QP目标函数值下降，求出方向p后，如果 $x_{k+1}=x_k+p$ 满足原QP里的所有约束，就将这个点作为下一个迭代点 ，如果不满足所有约束（朝p走的这一步可能会走的太大了，走出了可行域），则将步子迈的小一点，来使得所有约束条件满足，即给p加一个系数α，系数小于1。即

$$x_{k+1}=x_k+\alpha p \ \left\{\begin{aligned}&\alpha=1&&满足所有约束\\&0<\alpha<1&&有约束不满足\end{aligned}\right.$$

公式

假设求解的 QP 问题为

$$\min_xf(x)=\frac{1}{2}x^TGx+x^Tc\\A_ix\geq b,i\in I$$

则在工作集 W 的积极集约束满足的条件下的第 k 次迭代下的最优点为

$$f(x^\star )=f(x_k+p)\\=\frac{1}{2}(x_k+p)^TG(x_k+p)+(x_k+p)^Tc\\=\frac{1}{2}p^TGp+(Gx_k+c)^Tp+\frac{1}{2}x_k^TGx_k+x_kc\\subject~to~~A_i(x_k+p)=b_i,i\in W$$

上式中与 p 无关的变量可以看作是常数，不需要管？也就是优化下列式子

$$\min \frac{1}{2}p^TGp+(Gx+c)^Tp\\A_ip=0,i\in W$$

解出 p 后，下一个迭代点

$$x_{k+1}=x_k+\alpha p$$

然后就是考虑工作集之外的约束条件的满足情况，因为工作集内的约束已经考虑过，所有条件满足。首先判断 $A_ip$ 符号，若 $A_ip\geq 0$ 则可以知道它满足所有约束，因为

$$A_ix_{k+1}=A_i(x_k+\alpha p)\geq b,\alpha >0$$

如果 $A_ip\leq 0$ 则为了满足 $A_i(x_k+\alpha p)\geq b$ 条件，可以得到

$$\alpha \leq \frac{b-A_ix_k}{A_ip}$$

所以可得

$$\alpha =\min(1,\min\frac{b-A_ix_k}{A_ip})$$

就是沿着工作集下的active的可行域边界走，如果某次迭代没有约束条件（工作集为空），就朝着无约束下最优点在可行域内走，走到新的边界，然后将新的边界约束加入到工作集中，再沿着新的边界走，不断迭代，直到找到最优解。找到最优解的条件是 $x_k$满足KKT条件，即所有的 $\lambda$ 都大于0，则说明当前迭代点为最优解，退出迭代

其中求 $\lambda$ 的公式为

$$\partial f(x)=Gx+c\\A_ix\geq b,i\in I$$

看作等式约束时，可以使用 lagrange 乘子法

$$\partial L=Gx+c-\lambda A_i=0,i\in W$$

则可以得到

$$A_i\lambda =Gx+c$$

Active set method介绍 - 知乎 (zhihu.com)

Karush-Kuhn-Tucker (KKT)条件 - 知乎 (zhihu.com)

优化理论——二次规划 - 知乎 (zhihu.com)

KKT条件，原来如此简单 | 理论+算例实践 - 知乎 (zhihu.com)