github仓库
比例谐振控制算法分析 - 百度文库 (baidu.com)
前言
在传统的矢量控制系统中,广泛的采用了坐标变换技术,将三相静止坐标系下的电流电压等正弦量转化为同步旋转坐标系下的直流量,这个实现了简化系统,并且能够很好的使电机实现解耦控制。这么做的原因就是 PI 控制器无法对正弦量实现无静差控制,坐标变换简化了系统外环控制的设计,却造成内环结构复杂,设计困难。而且在电机运行中,电机的电感,电阻等电机参数会随着磁路的饱和,温度的升高而发生改变,从而使交叉耦合项不准确,进而使系统的控制精度下降。
PR 控制器可以实现对交流的无静差控制,将 PR 控制器用于网侧变换器的控制系统中,可以在两个相对静止的坐标系下对电流进行调节,可以简化控制过程中的坐标变换,消除电流 d,q 轴分量之间的耦合关系,并且可以忽略电网电压对系统的扰动作用。并且使用 PR 控制器更容易实现低次滤波补偿,这些都有利于简化系统的结构
傅里叶变换
F ( ω ) = ∫ − ∞ ∞ f ( t ) e − j ω t d t f ( t ) = 1 2 π ∫ − ∞ ∞ F ( ω ) e j ω t d ω F(\omega)=\int_{-\infty}^{\infty}f(t)e^{-j\omega t}dt\\f(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}F(\omega)e^{j\omega t}d\omega
F ( ω ) = ∫ − ∞ ∞ f ( t ) e − j ω t d t f ( t ) = 2 π 1 ∫ − ∞ ∞ F ( ω ) e j ω t d ω
laplace 变换
F ( s ) = ∫ − ∞ ∞ f ( t ) e − s t d t f ( t ) = 1 2 π j ∫ σ − j ∞ σ + j ∞ F ( s ) e s t d s F(s)=\int_{-\infty}^{\infty}f(t)e^{-st}dt\\f(t)=\frac{1}{2\pi j}\int_{\sigma-j\infty}^{\sigma+j\infty}F(s)e^{st}ds
F ( s ) = ∫ − ∞ ∞ f ( t ) e − s t d t f ( t ) = 2 π j 1 ∫ σ − j ∞ σ + j ∞ F ( s ) e s t d s
z 变换
F(z)=\sum f[n]z^{-n}\\f[n]=\frac{1}{2\pi j}\textcircled{\int} F(z)z^{n-1}dz
小结
上述三种变换可以利用如下映射关系实现传递函数之间的等价转换
s = j ω = 1 T ln z z = e s T = e j ω T s=j\omega=\frac{1}{T}\ln z\\z=e^{sT}=e^{j\omega T}
s = j ω = T 1 ln z z = e s T = e j ω T
稳定性分析
· 连续型传递函数稳定的充要条件为,所有极点均位于 s 域左半平面;离散型传递函数稳定的充要条件为,所有极点均位于 z 域原点为圆心的单位圆内。对于连续传函离散化问题,s 域左半平面所有极点,经 z = e s T z=e^{sT} z = e s T
PR 控制器
介绍
PR 控制器即比例谐振控制器,由比例环节和谐振环节组成,可对正弦量实现无静差控制。理想 PR 控制器的传递函数如下
G ( s ) = K P + K R s s 2 + w 0 2 G(s)=K_P+\frac{K_Rs}{s^2+w_0^2}
G ( s ) = K P + s 2 + w 0 2 K R s
其中
K P K_P K P K R K_R K R w 0 w_0 w 0
PR 控制器中的积分环节又称为广义积分器,可以对谐振频率的正弦量进行幅值积分
小例子
对于同频的输入信号 M sin ( ω t + φ ) M\sin(\omega t+\varphi) M sin ( ω t + φ )
L ( M sin ( ω t + φ ) ) = M cos ( φ ) ω s 2 + ω 2 + M sin ( φ ) s s 2 + ω 2 L(M\sin(\omega t+\varphi))=M\cos(\varphi)\frac{\omega}{s^2+\omega^2}+M\sin(\varphi)\frac{s}{s^2+\omega^2}
L ( M sin ( ω t + φ ) ) = M cos ( φ ) s 2 + ω 2 ω + M sin ( φ ) s 2 + ω 2 s
经过谐振项之后,表示变为(其中 ω 0 = ω \omega_0=\omega ω 0 = ω
K R s s 2 + w 0 2 ( M cos ( φ ) ω s 2 + ω 2 + M sin ( φ ) s s 2 + ω 2 ) = K R M ( cos ( φ ) ω s ( s 2 + ω 2 ) 2 + sin ( φ ) s 2 ( s 2 + ω 2 ) 2 ) = K R M ( cos ( φ ) ω s ( s 2 + ω 2 ) 2 + sin ( φ ) 2 ( 1 s 2 + ω 2 + s 2 − w 2 ( s 2 + ω 2 ) 2 ) ) \frac{K_Rs}{s^2+w_0^2}(M\cos(\varphi)\frac{\omega}{s^2+\omega^2}+M\sin(\varphi)\frac{s}{s^2+\omega^2})\\=K_RM(\cos(\varphi)\frac{\omega s}{(s^2+\omega^2)^2}+\sin(\varphi)\frac{s^2}{(s^2+\omega^2)^2})\\=K_RM(\cos(\varphi)\frac{\omega s}{(s^2+\omega^2)^2}+\frac{\sin(\varphi)}{2}(\frac{1}{s^2+\omega^2}+\frac{s^2-w^2}{(s^2+\omega^2)^2}))
s 2 + w 0 2 K R s ( M cos ( φ ) s 2 + ω 2 ω + M sin ( φ ) s 2 + ω 2 s ) = K R M ( cos ( φ ) ( s 2 + ω 2 ) 2 ω s + sin ( φ ) ( s 2 + ω 2 ) 2 s 2 ) = K R M ( cos ( φ ) ( s 2 + ω 2 ) 2 ω s + 2 sin ( φ ) ( s 2 + ω 2 1 + ( s 2 + ω 2 ) 2 s 2 − w 2 ) )
分别推导 t cos ( ω t ) t\cos(\omega t) t cos ( ω t ) t sin ( ω t ) t\sin(\omega t) t sin ( ω t )
L ( t cos ( ω t ) ) = s 2 − ω 2 ( s 2 + ω 2 ) L ( t sin ( ω t ) ) = 2 ω s ( s 2 + ω 2 ) 2 L(t\cos(\omega t))=\frac{s^2-\omega^2}{(s^2+\omega^2)}\\L(t\sin(\omega t))=\frac{2\omega s}{(s^2+\omega^2)^2}
L ( t cos ( ω t ) ) = ( s 2 + ω 2 ) s 2 − ω 2 L ( t sin ( ω t ) ) = ( s 2 + ω 2 ) 2 2 ω s
所以上式的拉普拉斯反变换为
K R M ( cos ( φ ) 2 t sin ( ω t ) + sin ( φ ) 2 ( t cos ( ω t ) + 1 ω sin ( ω t ) ) ) K_RM(\frac{\cos(\varphi)}{2}t\sin(\omega t)+\frac{\sin(\varphi)}{2}(t\cos(\omega t)+\frac{1}{\omega}\sin(\omega t)))
K R M ( 2 cos ( φ ) t sin ( ω t ) + 2 sin ( φ ) ( t cos ( ω t ) + ω 1 sin ( ω t ) ) )
整理之后得到
K R M 2 ( ( t cos ( φ ) + sin ( φ ) ω ) sin ( ω t ) + t sin ( φ ) cos ( ω t ) ) \frac{K_RM}{2}((t\cos(\varphi)+\frac{\sin(\varphi)}{\omega})\sin(\omega t)+t\sin(\varphi)\cos(\omega t))
2 K R M ( ( t cos ( φ ) + ω sin ( φ ) ) sin ( ω t ) + t sin ( φ ) cos ( ω t ) )
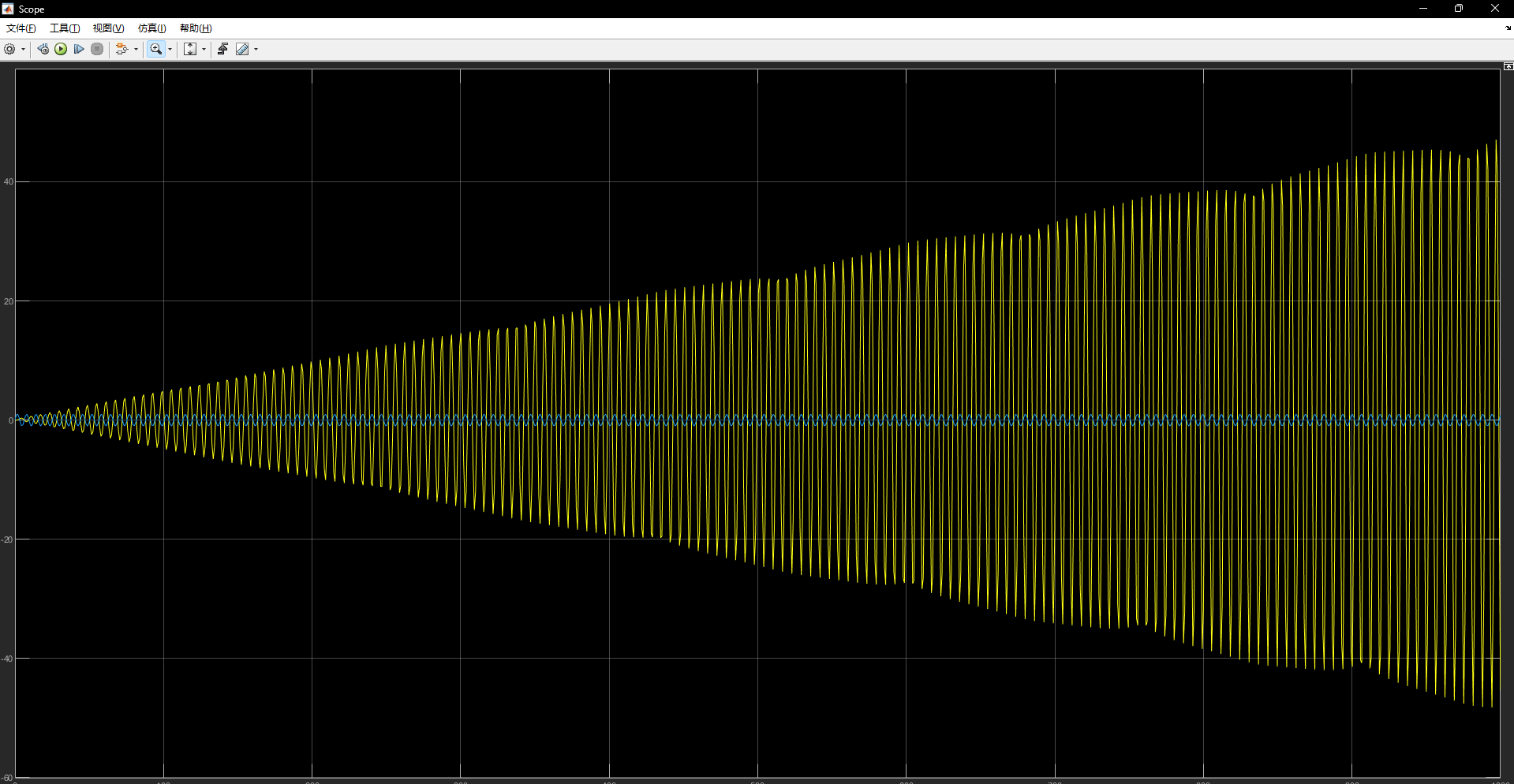
由上述可知,当 φ = 0 \varphi=0 φ = 0
K R M 2 t sin ( ω t ) \frac{K_RM}{2}t\sin(\omega t)
2 K R M t sin ( ω t )
如图,与输入信号相位相同,幅值呈时间线性上升
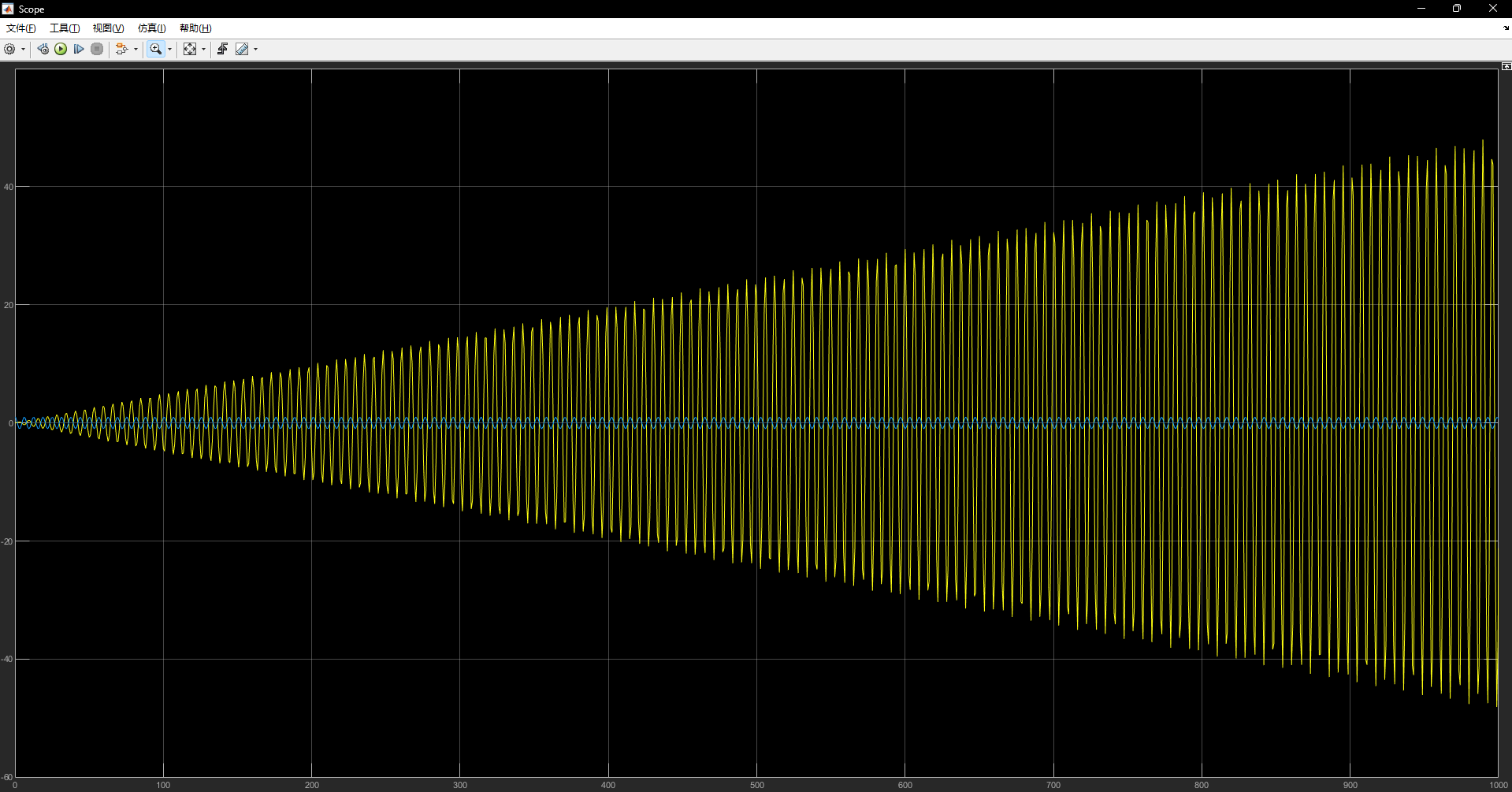
当 φ = 90 \varphi=90 φ = 9 0
K R M 2 ( sin ( ω t ) ω + t cos ( ω t ) ) \frac{K_RM}{2}(\frac{\sin(\omega t)}{\omega}+t\cos(\omega t))
2 K R M ( ω sin ( ω t ) + t cos ( ω t ) )
当时间稍大时,该值贴近于 t cos ( ω t ) t\cos(\omega t) t cos ( ω t )
如下图所示,当 PR 控制器中的积分部分 K R s s 2 + w 0 2 \frac{K_Rs}{s^2+w_0^2} s 2 + w 0 2 K R s
参数对控制器的影响
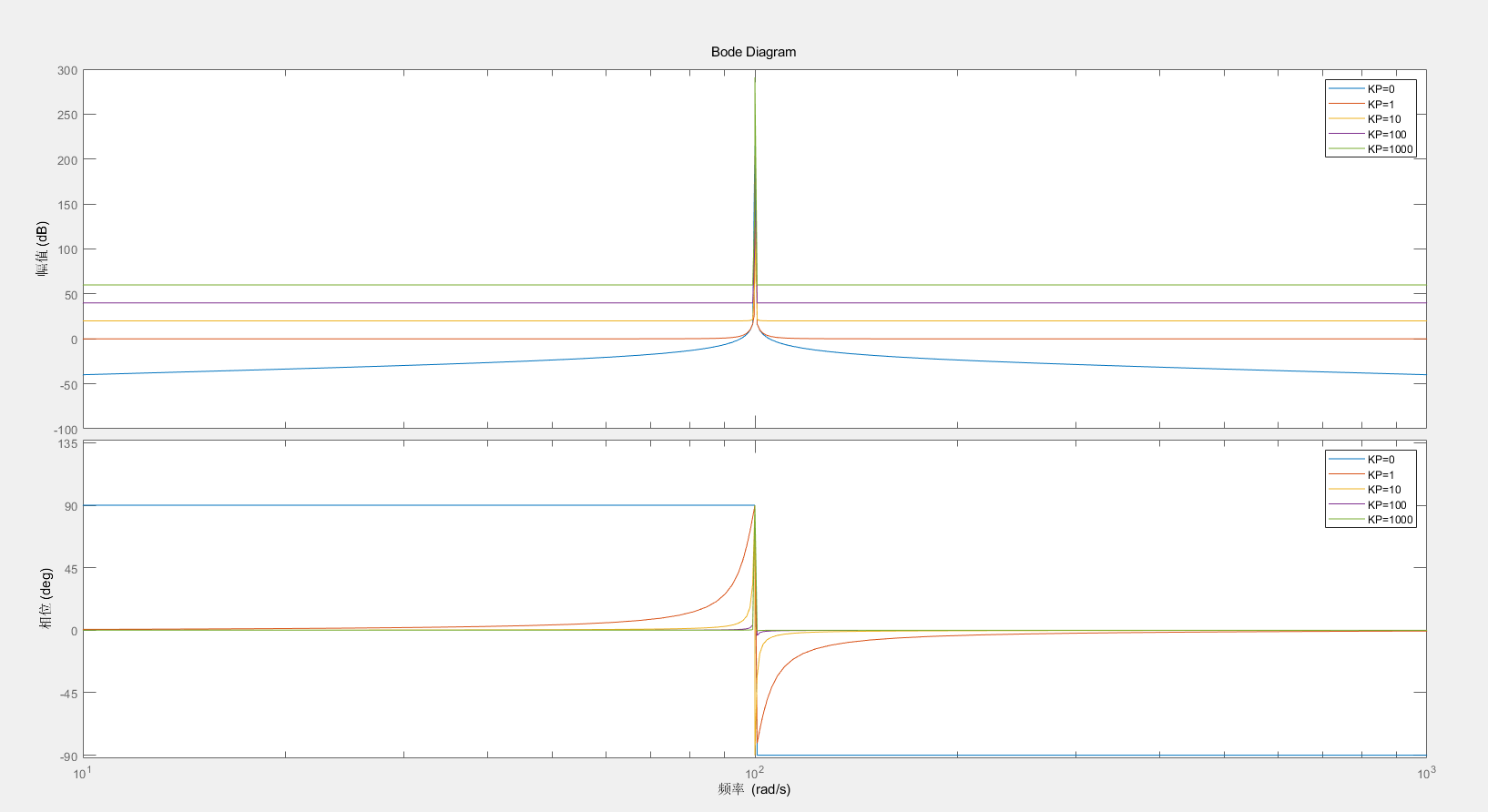
K P K_P K P
选取 K R = 1 , ω 0 = 100 K_R=1, \omega_0=100 K R = 1 , ω 0 = 1 0 0
K P K_P K P ω c \omega_c ω c
K R K_R K R
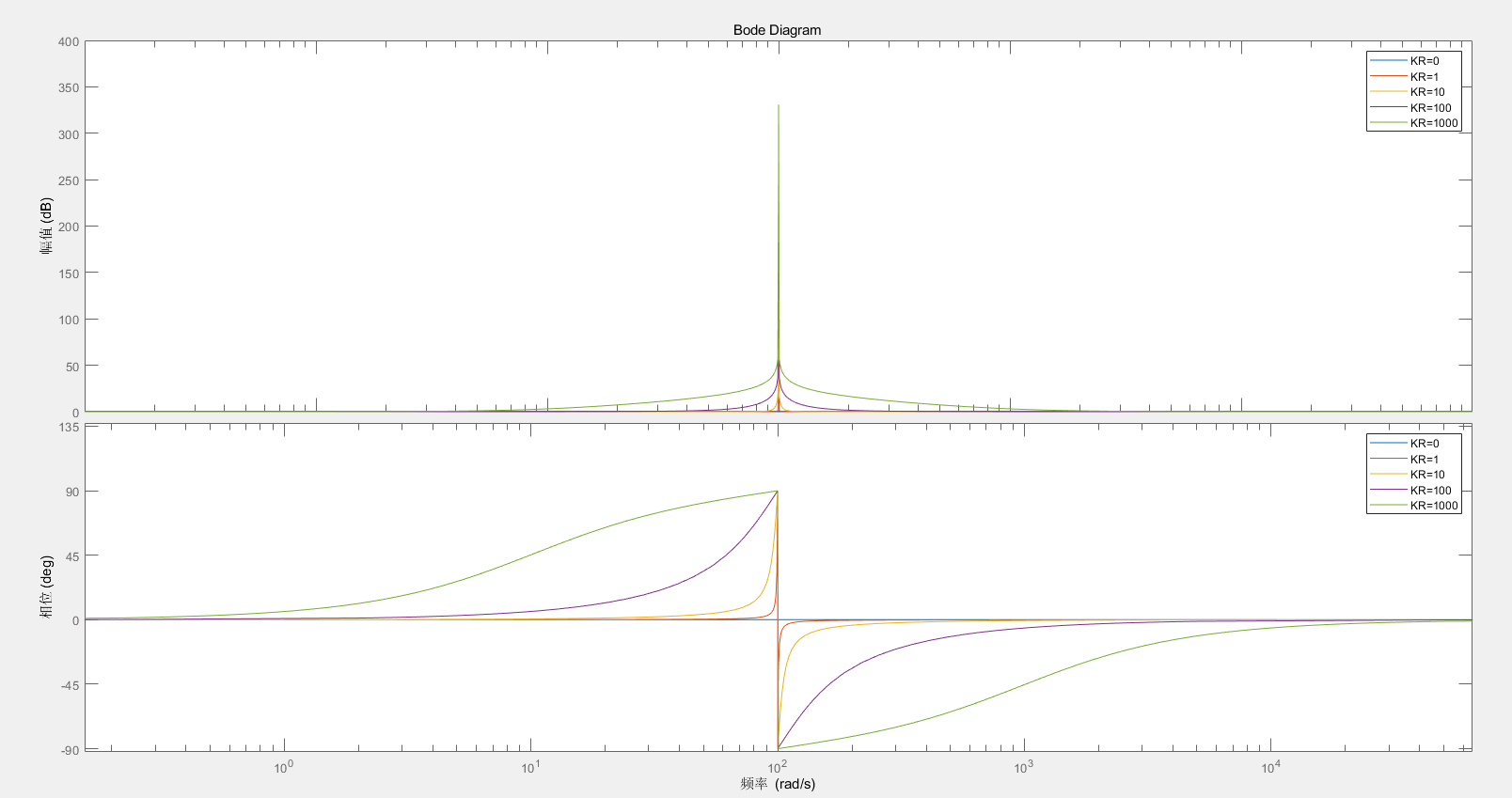
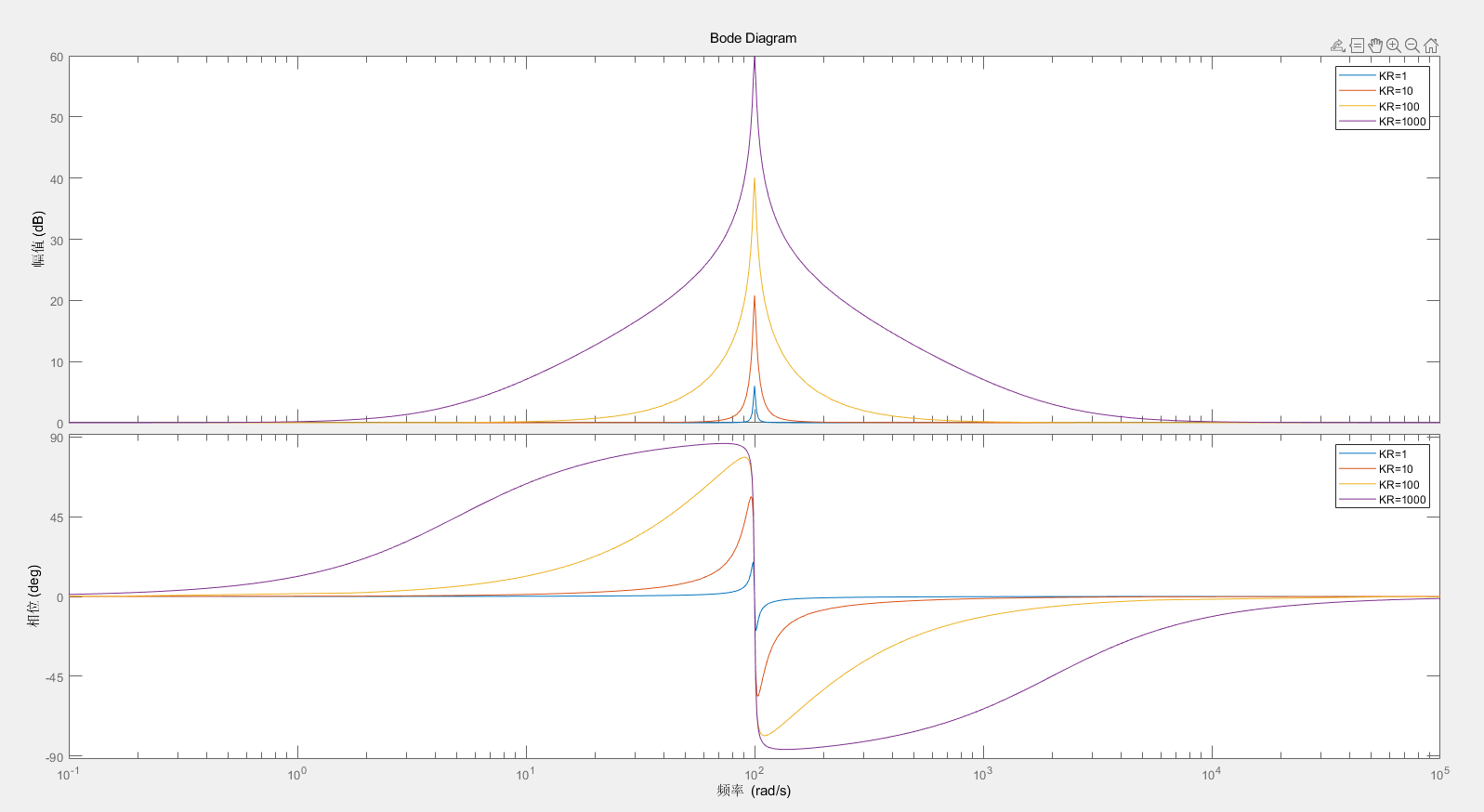
选取 K P = 1 , ω 0 = 100 K_P=1, \omega_0=100 K P = 1 , ω 0 = 1 0 0
可见 K R K_R K R K R K_R K R K R K_R K R ω 0 \omega_0 ω 0
ω 0 \omega_0 ω 0
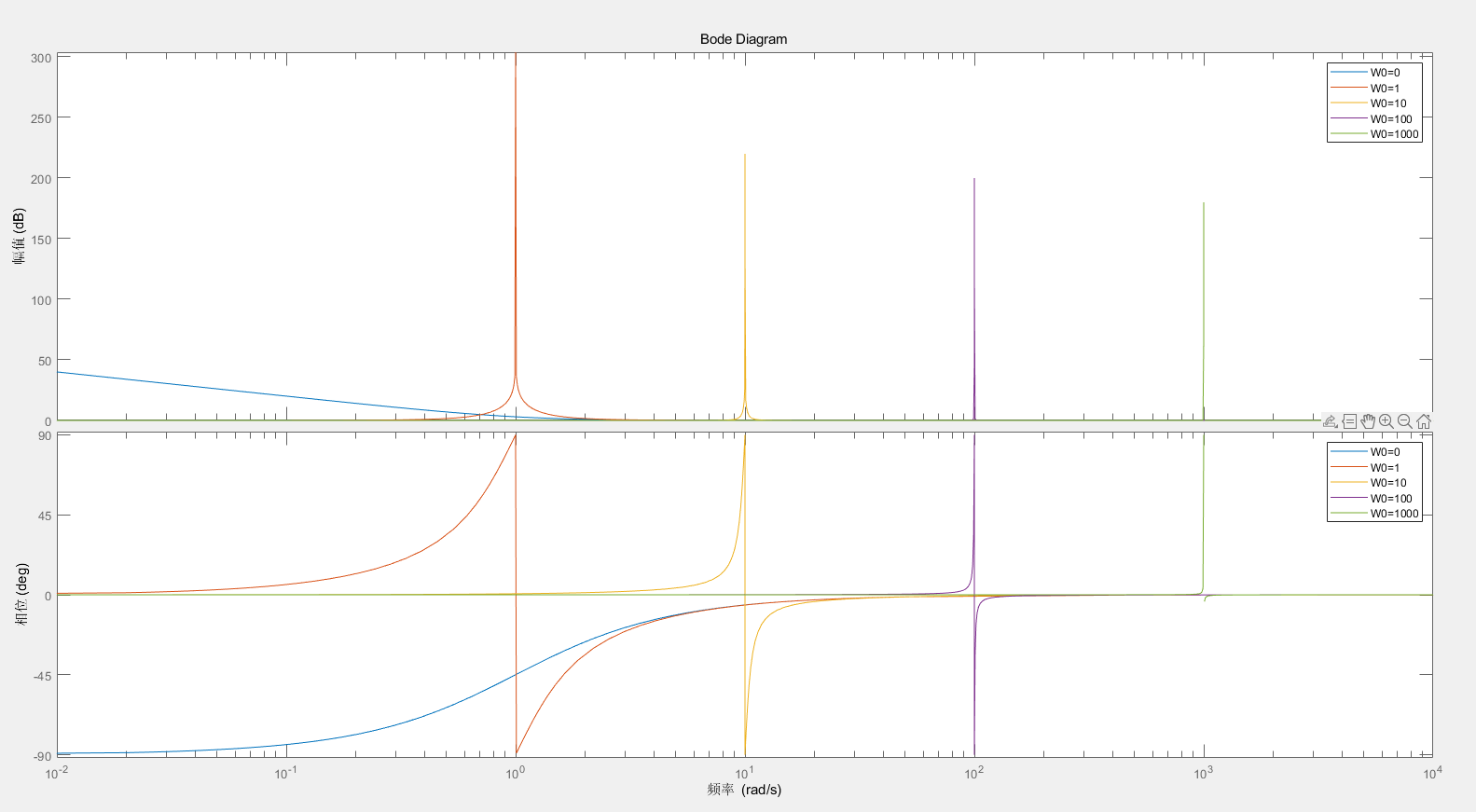
选取 K P = 1 , K R = 1 K_P=1,K_R=1 K P = 1 , K R = 1
可见, ω 0 \omega_0 ω 0 ω 0 \omega_0 ω 0
准 PR 控制器
介绍
与 PI 控制器相比,PR 控制器可以达到零稳态误差,提高有选择地抗电网电压干扰的能力,但是在实际的使用中,PR 控制器的实现存在两个问题
由于模拟系统元器件参数精度和数字系统精度的限制,PR 控制器不容易实现
PR 控制器在非基频处的增益非常小,当电网频率产生偏移时,就无法有效抑制电网产生的谐波
因此,在 PR 的基础上,提出了一种容易实现的准 PR 控制器,既可以保持 PR 控制器的高增益,同时还可以有效减小电网频率偏移对逆变器输出电感电流的影响
准 PR 控制器传递函数为
G ( s ) = K P + 2 K R ω c s s 2 + 2 ω c s + ω 0 2 G(s)=K_P+\frac{2K_R\omega_cs}{s^2+2\omega_cs+\omega_0^2}
G ( s ) = K P + s 2 + 2 ω c s + ω 0 2 2 K R ω c s
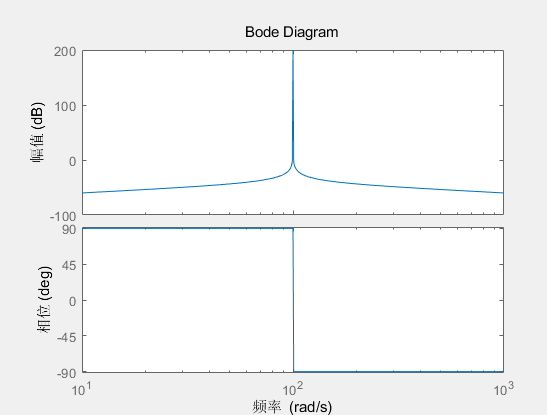
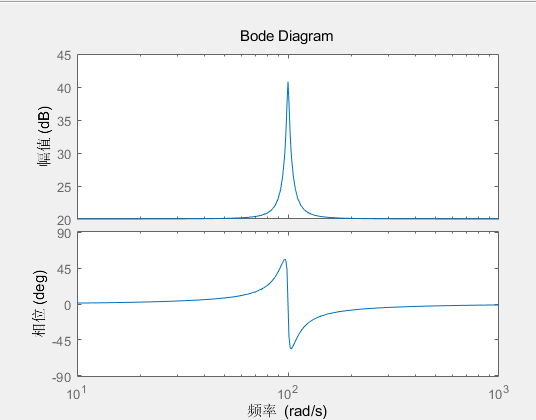
控制器的伯德图如下所示,选择参数
K P = 10 K R = 100 ω 0 = 100 ω c = 1 K_P=10\\K_R=100\\\omega_0=100\\\omega_c=1
K P = 1 0 K R = 1 0 0 ω 0 = 1 0 0 ω c = 1
参数设置
除了比例系数之外,准 PR 控制器还有 K R , ω c K_R,\omega_c K R , ω c
ω c = 0 \omega_c=0 ω c = 0 K R K_R K R
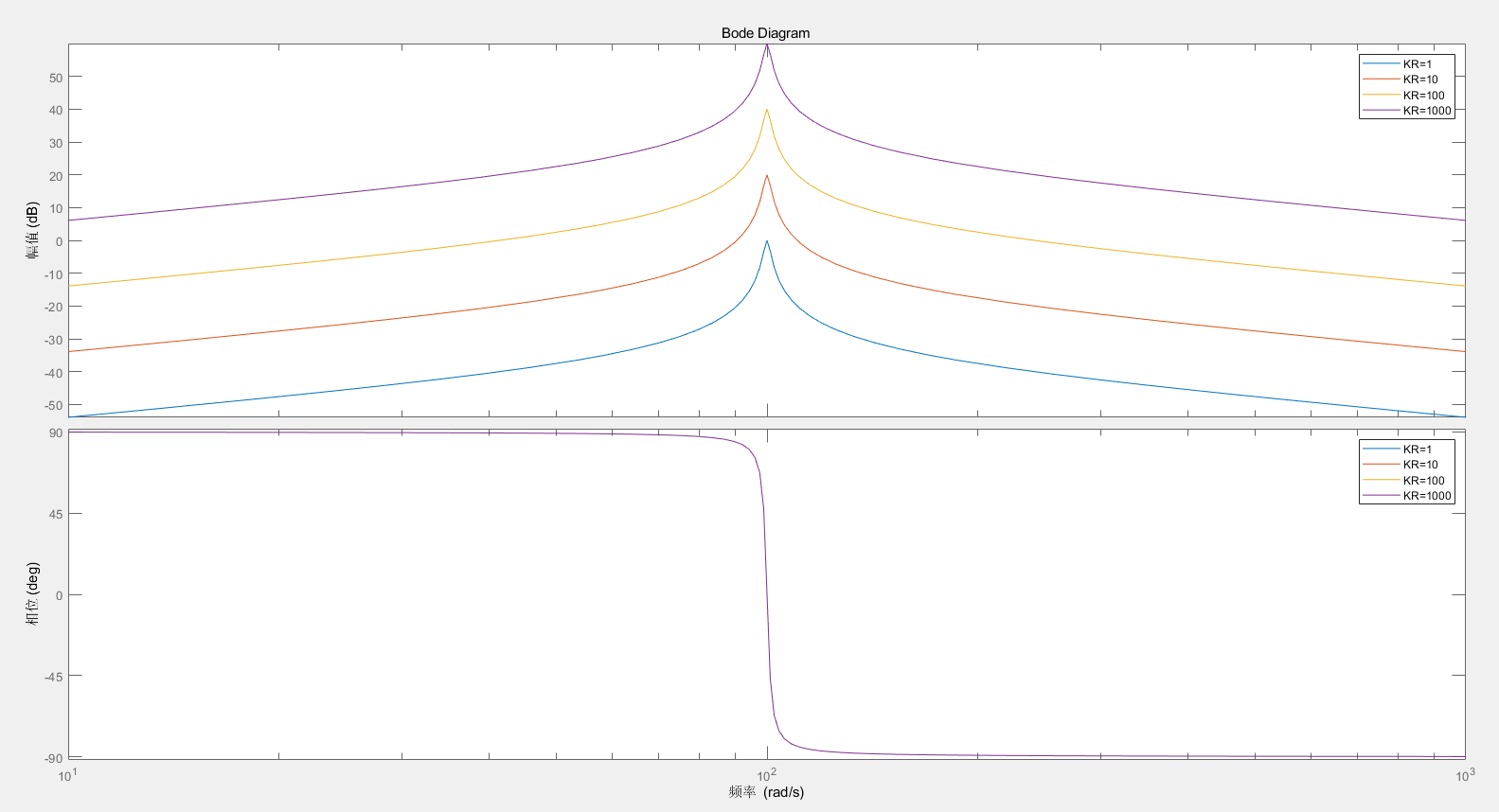
从图中可以看出,当 K R K_R K R
但是当有比例项的时候,带宽也不是一定的,会与 K P K_P K P
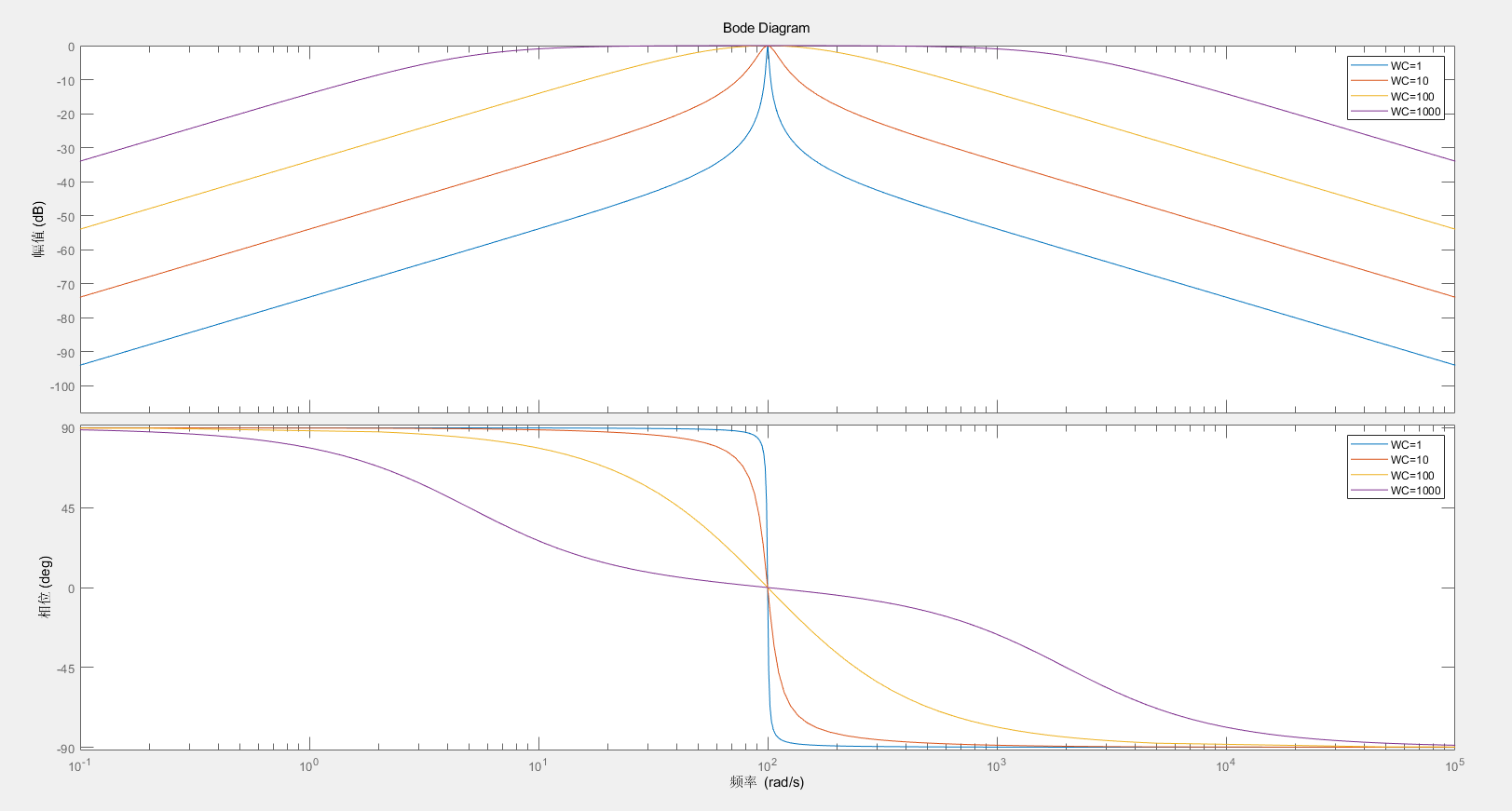
K R = 1 K_R=1 K R = 1 ω c \omega_c ω c
如图可知, ω c \omega_c ω c ω c \omega_c ω c K R K_R K R s = j ω s=j\omega s = j ω
G ( j ω ) = 2 K R ω c j ω − ω 2 + 2 ω c j ω + ω 0 2 G(j\omega)=\frac{2K_R\omega_cj\omega}{-\omega^2+2\omega_cj\omega+\omega_0^2}
G ( j ω ) = − ω 2 + 2 ω c j ω + ω 0 2 2 K R ω c j ω
根据对带宽的定义, ∣ G ( j ω ) ∣ = K R ( 2 ) |G(j\omega)|=\frac{K_R}{\sqrt(2)} ∣ G ( j ω ) ∣ = ( 2 ) K R ∣ ω 2 − ω 0 2 2 w c w ∣ = 1 |\frac{\omega^2-\omega_0^2}{2w_cw}|=1 ∣ 2 w c w ω 2 − ω 0 2 ∣ = 1 ω c π H z \frac{\omega_c}{\pi}Hz π ω c H z
假设电网电压频率波动的允许的范围为 ± 0.8 H z \plusmn 0.8Hz ± 0 . 8 H z ω c π = 1.6 H z \frac{\omega_c}{\pi}=1.6Hz π ω c = 1 . 6 H z ω c = 5 H z \omega_c=5Hz ω c = 5 H z
准 PR 控制器的离散化
模拟控制器的离散化有两种方式,分别为脉冲响应不变法和双线性变换法
脉冲响应不变法
PR 控制器的数字实现方法主要有两种,分别是采用 Z 算符和采用 δ \delta δ
G ( s ) = 2 K R ω c s s 2 + 2 ω c s + ω 0 2 = 2 K R ω c s ( s − − 2 ω c + 4 ω c 2 − 4 ω 0 2 2 ) ( s − − 2 ω c − 4 ω c 2 − 4 ω 0 2 2 ) = 2 K R ω c s ( s + ω c − ω c 2 − ω 0 2 ) ( s + ω c + ω c 2 − ω 0 2 ) = A s + ω c − ω c 2 − ω 0 2 + B s + ω c + ω c 2 − ω 0 2 G(s)=\frac{2K_R\omega_cs}{s^2+2\omega_cs+\omega_0^2}\\=\frac{2K_R\omega_cs}{(s-\frac{-2\omega_c+\sqrt{4\omega_c^2-4\omega_0^2}}{2})(s-\frac{-2\omega_c-\sqrt{4\omega_c^2-4\omega_0^2}}{2})}\\=\frac{2K_R\omega_cs}{(s+\omega_c-\sqrt{\omega_c^2-\omega_0^2})(s+\omega_c+\sqrt{\omega_c^2-\omega_0^2})}\\=\frac{A}{s+\omega_c-\sqrt{\omega_c^2-\omega_0^2}}+\frac{B}{s+\omega_c+\sqrt{\omega_c^2-\omega_0^2}}
G ( s ) = s 2 + 2 ω c s + ω 0 2 2 K R ω c s = ( s − 2 − 2 ω c + 4 ω c 2 − 4 ω 0 2 ) ( s − 2 − 2 ω c − 4 ω c 2 − 4 ω 0 2 ) 2 K R ω c s = ( s + ω c − ω c 2 − ω 0 2 ) ( s + ω c + ω c 2 − ω 0 2 ) 2 K R ω c s = s + ω c − ω c 2 − ω 0 2 A + s + ω c + ω c 2 − ω 0 2 B
其中
A = K R ω c ( 1 − ω c ω c 2 − ω 0 2 ) B = K R ω c ( 1 + ω c ω c 2 − ω 0 2 ) A=K_R\omega_c(1-\frac{\omega_c}{\sqrt{\omega_c^2-\omega_0^2}})\\B=K_R\omega_c(1+\frac{\omega_c}{\sqrt{\omega_c^2-\omega_0^2}})
A = K R ω c ( 1 − ω c 2 − ω 0 2 ω c ) B = K R ω c ( 1 + ω c 2 − ω 0 2 ω c )
上式通过脉冲响应不变法转为 Z 变换,Z 变换实际上就是连续系统离散化的结果,在 matlab 中使用函数
1 2 F = (2 * KR * WC * s) / (s ^ 2 + 2 * WC * s + W0 ^ 2 ); c2d(F, t, 'z' );
得到
G ( z ) = A z z − e − ( ω c − ω c 2 − ω 0 2 ) T + B z z − e − ( ω c + ω c 2 − ω 0 2 ) T = A 1 − z − 1 e − ( ω c − ω c 2 − ω 0 2 ) T + B 1 − z − 1 e − ( ω c + ω c 2 − ω 0 2 ) T G(z)=\frac{Az}{z-e^{-(\omega_c-\sqrt{\omega_c^2-\omega_0^2})T}}+\frac{Bz}{z-e^{-(\omega_c+\sqrt{\omega_c^2-\omega_0^2})T}}\\=\frac{A}{1-z^{-1}e^{-(\omega_c-\sqrt{\omega_c^2-\omega_0^2})T}}+\frac{B}{1-z^{-1}e^{-(\omega_c+\sqrt{\omega_c^2-\omega_0^2})T}}
G ( z ) = z − e − ( ω c − ω c 2 − ω 0 2 ) T A z + z − e − ( ω c + ω c 2 − ω 0 2 ) T B z = 1 − z − 1 e − ( ω c − ω c 2 − ω 0 2 ) T A + 1 − z − 1 e − ( ω c + ω c 2 − ω 0 2 ) T B
设
C = e − ( ω c − ω c 2 − ω 0 2 ) T D = e − ( ω c + ω c 2 − ω 0 2 ) T C=e^{-(\omega_c-\sqrt{\omega_c^2-\omega_0^2})T}\\D=e^{-(\omega_c+\sqrt{\omega_c^2-\omega_0^2})T}
C = e − ( ω c − ω c 2 − ω 0 2 ) T D = e − ( ω c + ω c 2 − ω 0 2 ) T
则有
G ( z ) = A z 1 − z − 1 C + B z 1 − z − 1 D = ( A + B ) − ( A D − B C ) z − 1 1 − ( C + D ) z − 1 + C D z − 2 G(z)=\frac{Az}{1-z^{-1}C}+\frac{Bz}{1-z^{-1}D}\\=\frac{(A+B)-(AD-BC)z^{-1}}{1-(C+D)z^{-1}+CDz^{-2}}
G ( z ) = 1 − z − 1 C A z + 1 − z − 1 D B z = 1 − ( C + D ) z − 1 + C D z − 2 ( A + B ) − ( A D − B C ) z − 1
设 Y = G X Y=GX Y = G X
y ( n ) = ( C + D ) y ( n − 1 ) − C D y ( n − 2 ) + ( A + B ) x ( n ) − ( A D − B C ) x ( n − 1 ) y(n)=(C+D)y(n-1)-CDy(n-2)+(A+B)x(n)-(AD-BC)x(n-1)
y ( n ) = ( C + D ) y ( n − 1 ) − C D y ( n − 2 ) + ( A + B ) x ( n ) − ( A D − B C ) x ( n − 1 )
其中
A = K R ω c ( 1 − ω c ω c 2 − ω 0 2 ) B = K R ω c ( 1 + ω c ω c 2 − ω 0 2 ) C = e − ( ω c − ω c 2 − ω 0 2 ) T D = e − ( ω c + ω c 2 − ω 0 2 ) T A=K_R\omega_c(1-\frac{\omega_c}{\sqrt{\omega_c^2-\omega_0^2}})\\B=K_R\omega_c(1+\frac{\omega_c}{\sqrt{\omega_c^2-\omega_0^2}})\\C=e^{-(\omega_c-\sqrt{\omega_c^2-\omega_0^2})T}\\D=e^{-(\omega_c+\sqrt{\omega_c^2-\omega_0^2})T}
A = K R ω c ( 1 − ω c 2 − ω 0 2 ω c ) B = K R ω c ( 1 + ω c 2 − ω 0 2 ω c ) C = e − ( ω c − ω c 2 − ω 0 2 ) T D = e − ( ω c + ω c 2 − ω 0 2 ) T
例子
对于一个一阶系统
G ( s ) = 1 s + 1 G(s)=\frac{1}{s+1}
G ( s ) = s + 1 1
跟踪一个正弦信号量 sin ( 100 π t ) \sin(100\pi t) sin ( 1 0 0 π t )
K p = 1000 K R = 5000 ω c = 10 π w 0 = 100 π K i = 500 K_p=1000\\K_R=5000\\\omega_c=10\pi\\w_0=100\pi\\K_i=500
K p = 1 0 0 0 K R = 5 0 0 0 ω c = 1 0 π w 0 = 1 0 0 π K i = 5 0 0
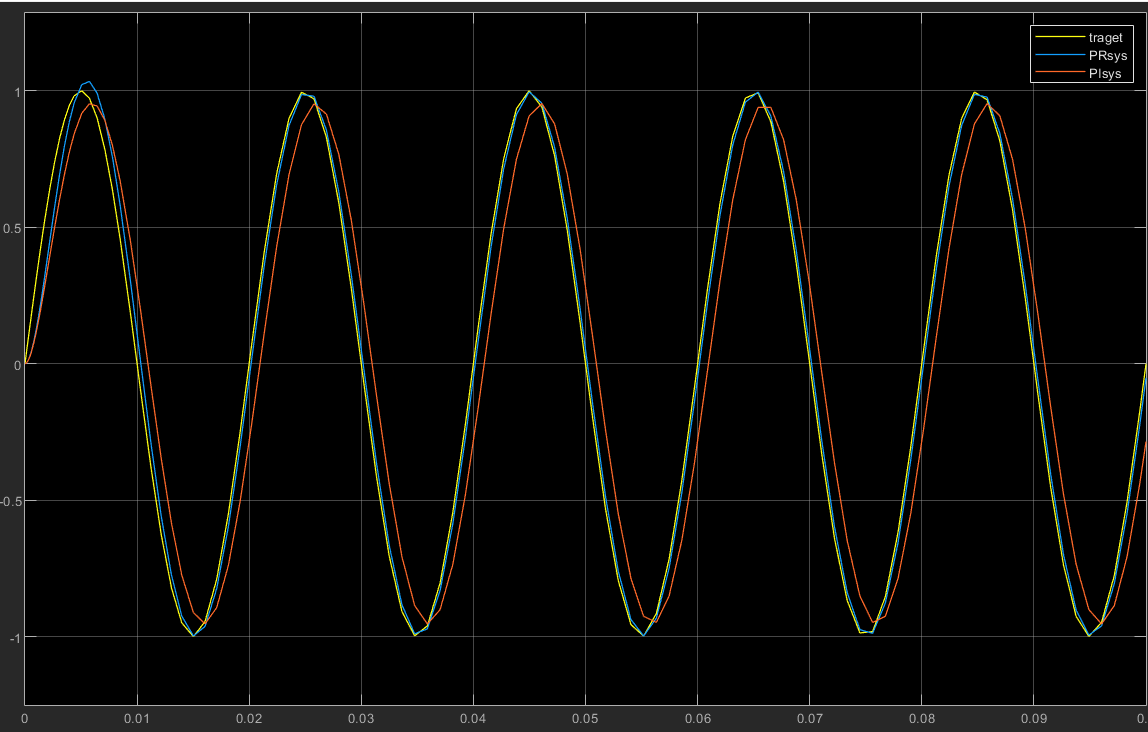
最终得到的结果为
可见 PR 控制器对于高频信号的跟踪要比 PI 控制器好,这是因为 PI 控制器中的 i 项需要累计误差才能有效果,而对于高频信号变化太快,导致累计误差很小而影响小