一个最优的控制策略是无论最初状态和最初的决策是什么，剩余的控制策略一定符合最优控制策略

需要考虑的问题

性能指标

假设一个系统中的状态量分别为 x1,…,xnx_1,…,x_n，并且期望值 x1d,…,xndx_{1d},…,x_{nd} ，可以得到性能指标，这里的状态量指的是一个状态在不同的时间下的具体表现

J=(x1−x1d)2+...+(xn−xnd)2J=(x_1-x_{1d})^2+...+(x_n-x_{nd})^2

体现的是每个状态变量的代价，也就是代价函数，当 J→0J→0 也就是说明状态与期望状态越接近，上式还可以写作另一种形式，令 en=xnd−xne_n=x_{nd}-x_n

J=[e1...en][e1...en]J=\begin{bmatrix}e_1&...&e_n\end{bmatrix}\begin{bmatrix}e_1\\...\\e_n\end{bmatrix}

由于对于不同的变量都有不同的权重系数，所以引入权重系数 ss

J=[e1...en][s1...sn][e1...en]=ETSEJ=\begin{bmatrix}e_1&...&e_n\end{bmatrix}\begin{bmatrix}s_1\\&...\\&&s_n\end{bmatrix}\begin{bmatrix}e_1\\...\\e_n\end{bmatrix}=E^TSE

由于不同的变量的单位不同，所以要将不同的单位进行规范化，需要在设计权重时考虑到

物理硬约束

对于一个系统的来说，速度，位置都是一种约束，这是控制中需要考虑的

能耗

引入能耗之后，权重矩阵就变为

J=ETSE+UTRUJ=E^TSE+U^TRU

其中

U=[u1...un−1]U=\begin{bmatrix}u_1\\...\\u_{n-1}\end{bmatrix}

这就需要考虑能耗与性能之间的权重了，如果 S>>RS>>R 导致系统不考虑能耗，而 R>>SR>>S 则会导致系统为了节能会有很差的表现，甚至是不动

这里的能耗约束实际上属于是一种软约束

系统的能耗也一定在某一个范围内 u∈u∗u\in u^*

系统状态跟踪

在速度追踪时，由于系统的状态的目标值不再是一个单纯的点，而是一个函数关系

[x1d...xnd]→[p1(t)...pn(t)]\begin{bmatrix}x_{1d}\\...\\x_{nd}\end{bmatrix}\rightarrow\begin{bmatrix}p_{1}(t)\\...\\p_n(t)\end{bmatrix}

实现系统向着目标点跟踪，并且在代价函数中也会体现

J=∣∣xn−xnd∣∣2Sn+∑k=0n−1(∣∣xk−xkd∣∣2Qk+∣∣uk∣∣2R)J=||x_n-x_{nd}||^2S_n+\sum_{k=0}^{n-1}(||x_k-x_{kd}||^2Q_k+||u_k||^2R)

其中第一项为末端代价，第二项为过程代价

避障

这是与系统状态跟踪是相关联的，系统可以运行的区域为容许轨迹 p∗p^*

在定义轨迹函数 p 时，需要保证 p∈p∗p\in p^*

最优化控制

代价函数也可以写作

J=∑k=m+1nhd(xn,k)+∑k=0mgd(xk,uk,k)J=\sum_{k=m+1}^{n}h_d(x_n,k)+\sum_{k=0}^{m}g_d(x_k,u_k,k)

其中第一项表示最终目标量的权重，而第二项表示过程的权重，最后的目标就是找到一个合适的 uku_k 来使得系统状态向着目标值转换，并且使代价函数 JJ 最小

动态规划

实际上最优控制策略体现出一种动态规划

例子

一个无人机，从地面以最短时间上升到 10 m

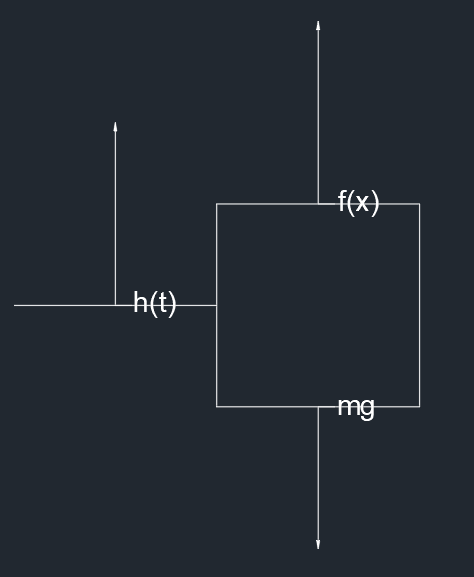
1708572807088.png

h(0)=0h˙(0)=0⇓h(tf)=10h˙(tf)=0h(0)=0\\\dot{h}(0)=0\\\Downarrow\\h(t_f)=10\\\dot{h}(t_f)=0

由于需要时间最短，可以设计代价函数

J=tfJ=t_f

约束（只能向上/静止）

−3≤a≤20≤v≤3-3\leq a\leq 2\\0\leq v\leq 3

列出系统状态方程

mh¨(t)=f(t)−mgf(t)=Fvmm\ddot{h}(t)=f(t)-mg\\f(t)=Fv_m

可以将系统离散化为多个状态

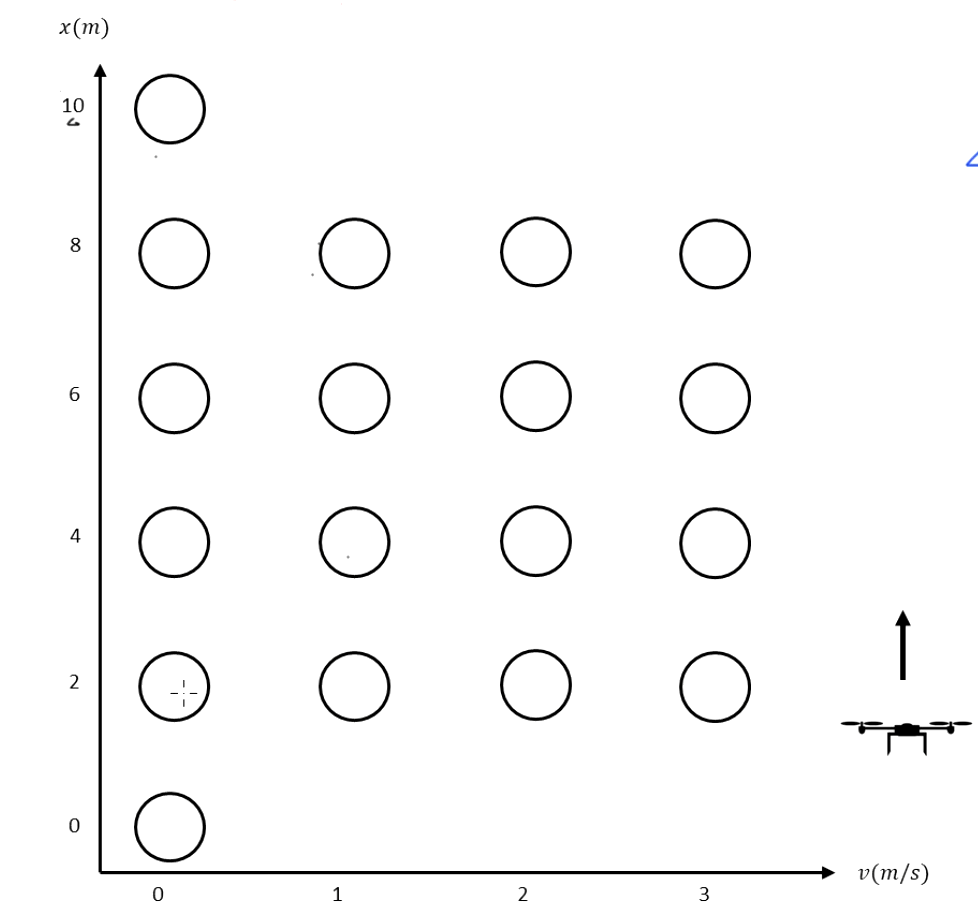
1708583538116.png

从终点开始，逐个计算每个状态所需的最小 cost to go，也就是将要的花费，从而得到最佳的速度路径规划

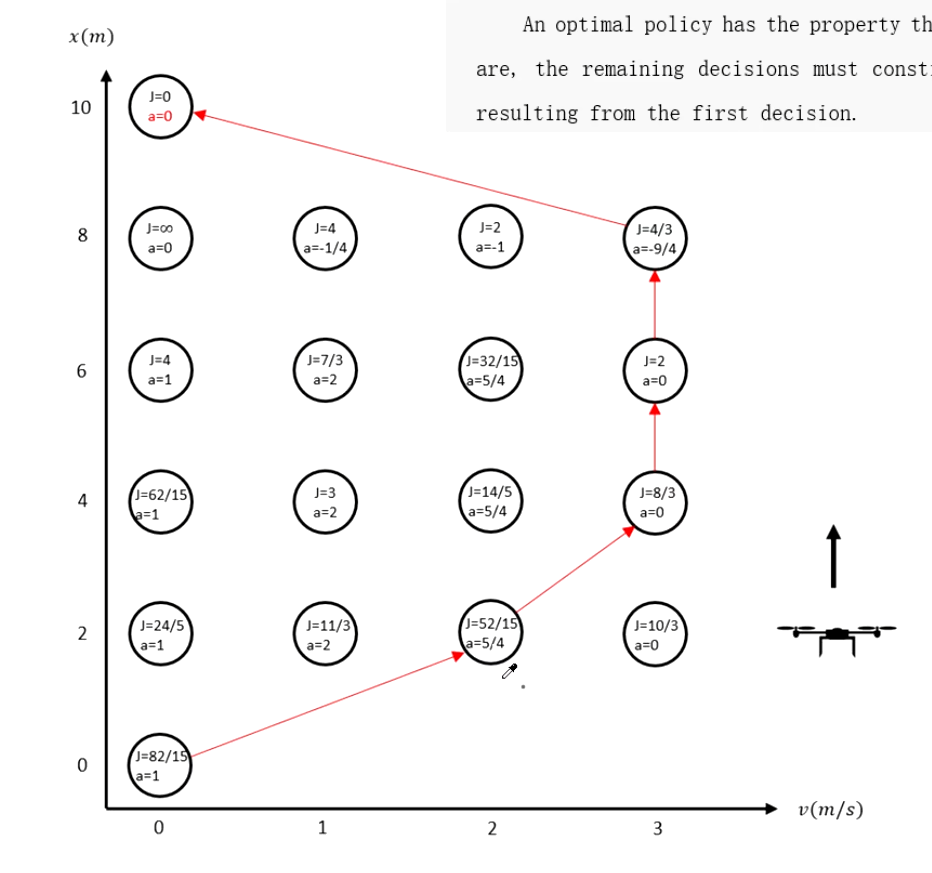
1708583966568.png

可以使用暴力算法直接解算出所有状态的代价函数，但是所需要的计算资源是不可估量的，所以要使用一个更简单的方法——动态规划

一个简单的例子

对于一个一维系统

xk+1=xk+ukx0=1xd=0x_{k+1}=x_k+u_k\\x_0=1\\x_d=0

设置代价函数

J=0.5∣∣xn−xnd∣∣2+0.5∑k=0n−1(∣∣xk−xkd∣∣2Qk+∣∣uk∣∣2R)⇓J=0.5x22+0.5(x12+u12+x02+u02)J=0.5||x_n-x_{nd}||^2+0.5\sum_{k=0}^{n-1}(||x_k-x_{kd}||^2Q_k+||u_k||^2R)\\\Downarrow\\J=0.5x_2^2+0.5(x_1^2+u_1^2+x_0^2+u_0^2)

可以提出两种策略

u0=−1  x1=x0+u0=0u1=0  x2=x1+u1=0⇓J=1u_0=-1~~x_1=x_0+u_0=0\\u_1=0~~x_2=x_1+u_1=0\\\Downarrow\\J=1

u0=−0.5  x1=x0+u0=0.5u1=−0.5  x2=x1+u1=0⇓J=0.875u_0=-0.5~~x_1=x_0+u_0=0.5\\u_1=-0.5~~x_2=x_1+u_1=0\\\Downarrow\\J=0.875

在这里就通过计算 u∗[0],u∗[1]u^*[0],u^*[1] 使代价函数最小，使用逆向分级的思想

J1→2=0.5x22+0.5x12+u12=0.5(x1+u1)2+0.5x12+0.5u12∂J∂u1=x1+u1+u1=0⇓u1∗=−12x1⇓J1→2∗=34x12⇓J0→2=0.5x22+0.5(x12+u12+x02+u02)=J1→2+0.5(x02+u02)J_{1\rightarrow 2}=0.5x_2^2+0.5x_1^2+u_1^2=0.5(x_1+u_1)^2+0.5x_1^2+0.5u_1^2\\\frac{\partial J}{\partial u_1}=x_1+u_1+u_1=0\\\Downarrow\\u^*_1=-\frac{1}{2}x_1\\\Downarrow\\J^*_{1\rightarrow 2}=\frac{3}{4}x_1^2\\\Downarrow\\J_{0\rightarrow 2}=0.5x_2^2+0.5(x_1^2+u_1^2+x_0^2+u_0^2)=J_{1\rightarrow 2}+0.5(x_0^2+u_0^2)

根据贝尔曼最优理论：当 J0→2J_{0\rightarrow 2} 最小，其中包含的 J1→2J_{1\rightarrow 2} 一定是最小的

J0→2=J1→2+0.5(x02+u02)=34x12+12(x02+u02)=34(x0+u0)2+12(x02+u02)∂J∂u0=32(x0+u0)+u0=0⇓u0∗=−35x0J_{0\rightarrow 2}=J_{1\rightarrow 2}+0.5(x_0^2+u_0^2)=\frac{3}{4}x_1^2+\frac{1}{2}(x_0^2+u_0^2)=\frac{3}{4}(x_0+u_0)^2+\frac{1}{2}(x_0^2+u_0^2)\\\frac{\partial J}{\partial u_0}=\frac{3}{2}(x_0+u_0)+u_0=0\\\Downarrow\\u_0^*=-\frac{3}{5}x_0

贝尔曼动态规划最优控制方程

JN−k→N∗(xN−k)=minuN−k(JN−(k−1)→N∗(f(xN−k,uN−k))+g(xN−k,uN−k))J^*_{N-k\rightarrow N}(x_{N-k})=\underset{u_{N-k}}{min}(J^*_{N-(k-1)\rightarrow N}(f(x_{N-k},u_{N-k}))+g(x_{N-k},u_{N-k}))