一点点小补充

M3508 转矩常数0.3，也就是每增加1A电流力矩增加0.3牛米
AK80-6 转矩常数 0.09 这个好像不用管

对于四足，电机相对，力矩Tp由TB和TF共同提供，会比以上计算更简单

五连杆正运动学解算

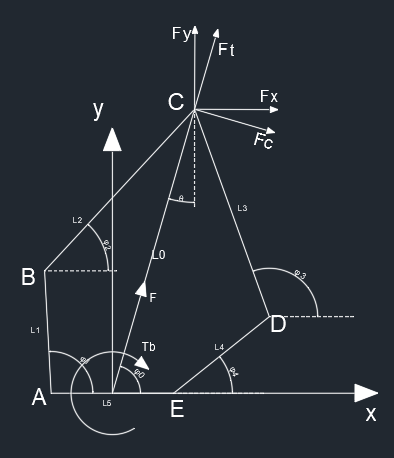
以杆 $L_5$ 的中心为原点，可以得到

$A=(-\frac{L_5}{2}, 0)\\B=(-\frac{L_5}{2}+L_1\cos\varphi_1,L_1\sin\varphi_1)\\D=(\frac{L_5}{2}+L_4\cos\varphi_4,L_4\sin\varphi_4)\\E=(\frac{L_5}{2},0)$

通过五连杆左右两部分列写 C 点坐标，可以得到下列等式

$\left\{\begin{aligned}&x_B+L_2\cos\varphi_2=x_D+L_3\cos\varphi_3\\&y_B+L_2\sin\varphi_2=y_D+L_3\sin\varphi_3\end{aligned}\right.$

求解得到

$\varphi_2=2\arctan(\frac{B+\sqrt{A^2+B^2-C^2}}{A+C})\\\varphi_3=\pi-2\arctan(\frac{-B+\sqrt{A^2+B^2-D^2}}{A+D})$

其中

$A=2L_2(x_D-x_B)\\B=2L_2(y_D-y_B)\\C=L_2^2+L_{BD}^2-L_3^2\\D=L_3^2+L_{BD}^2-L_2^2\\L_{BD}=\sqrt{(x_D-x_B)^2+(y_D-y_B)^2}$

可以得到 C 点坐标

$x_C=-\frac{L_5}{2}+L_1\cos(\varphi_1)+L_2\cos(\varphi_2)\\y_C=L_1\sin(\varphi_1)+L_2\sin(\varphi_2)$

则

$L_0=\sqrt{x_c^2+y_c^2}\\\varphi_0=\arctan{\frac{y_c}{x_c}}$

VMC

关键是在每个需要控制的自由度上构造合适的虚拟构件来产生合适的虚拟力。虚拟力不是实际执行机构的作用力或力矩，而是通过执行机构的作用经过机构转换而成。对于一些控制问题，我们可能需要将工作空间 (Task Space) 的力或力矩映射成关节空间 (Joint Space) 的关节力矩。

在五连杆中，需要获得机构末端沿腿的推力 $F$ 与沿中心轴的力矩 $T_b$，对应极坐标 $L_0,\varphi_0$ 与 $A,E$ 两个关节转动副力矩 $T_A,T_E$ 的关系。所以定义

$x=\begin{bmatrix}L_0\\\varphi_0\end{bmatrix}\\q=\begin{bmatrix}\varphi_1\\\varphi_4\end{bmatrix}$

对正运动学模型 $x=f(q)$ 做微分得

$f'=\begin{bmatrix}\frac{\partial L_0}{\partial \varphi_1}&\frac{\partial L_0}{\partial \varphi_4}\\\frac{\partial \varphi_0}{\partial \varphi_1}&\frac{\partial \varphi_0}{\partial \varphi_4}\end{bmatrix}$

这就是 x 对 q 的雅各比矩阵，记作 $J$。得到对应的全微分方程为

$\Delta x=J\Delta q$

通过雅各比矩阵 $J$ 将关节速度 $\dot{q}$ 映射为五连杆姿态变化率 $\dot{x}$。根据虚功原理，可以得到

$T^T\Delta q+(-F)^T\Delta x=0\\T=\begin{bmatrix}T_A\\T_E\end{bmatrix}\\F_{pole}=\begin{bmatrix}F\\T_b\end{bmatrix}$

将全微分方程带入之后可得

$T=J^TF_{pole}$

但是上述推导中的正运动学模型直接求雅各比矩阵比较困难，因为模型中有大量的平方与三角函数的运算，结果比较复杂。所以进行下列改进

由于雅各比矩阵实际上描述的是两坐标微分的线性映射关系，所以可以计算速度映射来得到雅各比矩阵。由于 $L_0,\varphi_0$ 实际上就是 $C$ 点的极坐标，所以首先求出 $C$ 点直角坐标速度

$\dot{x}_C=-L_1\dot{\varphi}_1\sin\varphi_1-L_2\dot{\varphi}_2\sin\varphi_2\\\dot{y}_C=L_1\dot{\varphi}_1\cos\varphi_1+L_2\dot{\varphi}_2\cos\varphi_2$

通过五连杆左右两部分列写 C 点坐标求导可以得到 $\dot\varphi_2$

$\left\{\begin{aligned}&\dot x_B-L_2\dot\varphi_2\sin\varphi_2=\dot x_D-L_3\dot\varphi_3\sin\varphi_3\\&y_B+L_2\sin\varphi_2=y_D+L_3\sin\varphi_3\end{aligned}\right.$

消去 $\dot\varphi_3$ 得到 $\dot\varphi_2$

$\dot\varphi_2=\frac{(\dot x_D-\dot x_B)\cos\varphi_3+(\dot y_D-\dot y_B)\sin\varphi_3}{L_2\sin(\varphi_3-\varphi_2)}$

其中

$\dot x_B=-L_2\dot\varphi_1\sin\varphi_1\\\dot y_B=L_2\dot\varphi_1\cos\varphi_1\\\dot x_D=-L_4\dot\varphi_4\sin\varphi_4\\\dot y_D=L_4\dot\varphi_4\sin\varphi_4$

并且其中的 $\dot\varphi_1,\dot\varphi_4$ 都是直接测出来的，带入之后得到

$\dot{x}_C=-L_1\dot{\varphi}_1\sin\varphi_1-L_2\frac{(\dot x_D-\dot x_B)\cos\varphi_3+(\dot y_D-\dot y_B)\sin\varphi_3}{L_2\sin(\varphi_3-\varphi_2)}\sin\varphi_2\\\dot{y}_C=L_1\dot{\varphi}_1\cos\varphi_1+L_2\frac{(\dot x_D-\dot x_B)\cos\varphi_3+(\dot y_D-\dot y_B)\sin\varphi_3}{L_2\sin(\varphi_3-\varphi_2)}\cos\varphi_2$

化简之后得到

$\begin{bmatrix}\dot x_C\\\dot y_C\end{bmatrix}=\begin{bmatrix}\frac{L_1\sin(\varphi_1-\varphi_2)\sin\varphi_3}{\sin(\varphi_2-\varphi_3)}&\frac{L_4\sin(\varphi_3-\varphi_4)\sin\varphi_2}{\sin(\varphi_2-\varphi_3)}\\-\frac{L_1\sin(\varphi_1-\varphi_2)\cos\varphi_3}{\sin(\varphi_2-\varphi_3)}&-\frac{L_4\sin(\varphi_3-\varphi_4)\cos\varphi_2}{\sin(\varphi_2-\varphi_3)}\end{bmatrix}\begin{bmatrix}\dot \varphi_1\\\dot \varphi_4\end{bmatrix}$

记作

$\begin{bmatrix}\dot x_C\\\dot y_C\end{bmatrix}=J\begin{bmatrix}\dot \varphi_1\\\dot \varphi_4\end{bmatrix}$

根据上式可以得到关节力矩 $T$ 与虚拟力 $F_{rect}$ 的关系

$T=J^TF_{rect}\\F_{rect}=\begin{bmatrix}F_x\\F_y\end{bmatrix}$

利用旋转矩阵将 $F_{rect}$ 旋转到杆的方向，旋转矩阵记作 $R$

$\begin{bmatrix}F_x\\F_y\end{bmatrix}=\begin{bmatrix}\cos\theta&\sin\theta\\-\sin\theta&\cos\theta\end{bmatrix}\begin{bmatrix}F_c\\F_t\end{bmatrix}$

将杆的方向里转到极坐标方向的力 $F_{pole}$，旋转矩阵记作 $M$

$\begin{bmatrix}F_c\\F_t\end{bmatrix}=\begin{bmatrix}0&\frac{1}{L_0}\\1&0\end{bmatrix}\begin{bmatrix}F\\T_b\end{bmatrix}$

依次带入得到最终的关节力矩与虚拟力之间的映射关系

$T=J^TRMF_{pole}$

令

$A=\frac{L_1\sin(\varphi_1-\varphi_2)}{\sin(\varphi_2-\varphi_3)}\\B=\frac{L_4\sin(\varphi_3-\varphi_4)}{\sin(\varphi_2-\varphi_3)}$

最终带入得到

$T=\begin{bmatrix}-A\cos(\theta+\varphi_3)&\frac{A\sin(\theta+\varphi_3)}{L_0}\\-B\cos(\theta+\varphi_2)&\frac{B\sin(\theta+\varphi_2)}{L_0}\end{bmatrix}F_{pole}$

但是在这里解算中的 $\varphi_0,\varphi_1,\varphi_2,\varphi_3, \varphi_4$ 都是逆时针为正的，所以最终得到的 $T$ 也是逆时针的，要施加到电机上需要取负值，因此最终结果为

$T=\begin{bmatrix}A\cos(\theta+\varphi_3)&-\frac{A\sin(\theta+\varphi_3)}{L_0}\\B\cos(\theta+\varphi_2)&-\frac{B\sin(\theta+\varphi_2)}{L_0}\end{bmatrix}F_{pole}$

注意，这里的·解算中，对于每个关节电机转矩的方向是顺时针为正，其他都是按照图上的方向的

Eigen::Matrix<float, 2, 2> trans;
float                      A = l1 * sin(angle1 - angle2) / sin(angle2 - angle3);
float                      B = l4 * sin(angle3 - angle4) / sin(angle2 - angle3);
trans << -A * cos(theta.now + angle3), 
			 A * sin(theta.now + angle3) / L0.now, 
         -B * cos(theta.now + angle2), 
         B * sin(theta.now + angle2) / L0.now;

this->jointF->setTorque(-trans(0, 0) * this->Fset - trans(0, 1) * this->Tbset);
this->jointB->setTorque(-trans(1, 0) * this->Fset - trans(1, 1) * this->Tbset);
this->wheel->setTorque(this->Twset);

虚功原理

理论力学次叙——虚功原理

是分析静力学中关键且重要的原理

一个原为静止的质点系，如果约束是理想双面定常约束，则系统继续保持静止的条件是所有作用于该系统的主动力对作用点的虚位移所作的功的和为零
在结构力学刚体体系中表述为：设满足理想约束的刚体体系上作用的任意平衡力系，又假设体系发生满足约束条件的无限小的刚体位移，则主动力在位移上所做的虚功总和恒为零
在结构力学变形体体系中表述为：体系在任意平衡力系作用下，给体系以几何可能的位移和变形，体系上所有外力所作的虚功总和恒等于体系各截面所有内力在微段变形上所作的虚功总和。

总之就是

当系统平衡且处于理想约束时，所有主动力的虚功之和为0
当系统平衡且处于理想约束时，外力的虚功等于内力的虚功

虚功 $\delta W$ 就是力在虚位移上做的功

则虚功原理表达式为

$\delta W_{in}(内力做的虚功) = \delta W_{ex}(外力做的虚功)$

或： $\sum_{i=1}^n F_i * \delta q_i=0\ (F 是主动力，矢量)$