github仓库
完整计算公式
output=kperrnow+kij=0∑kej+kd(errnow−errlast)
含义:
-
P: kperrnow
就是 kp 乘以此次误差,理论值与当前值的差值,作用是主动减小误差,使测量值主动贴近理论值。但是如果只有P的话,响应可能会非常剧烈,不好把控,P太大会导致超调
-
I: ki∑j=0kej
只要存在误差(稳态误差),不论误差有多小,i的输出也会越来越大
作用是消除稳态误差,当系统误差已经接近0时,p 的输出会很小,起不到继续减小误差的作用了,导致误差没有办法减小到0,这个时候就需要用到 I 算法,让误差值不断累积,并且累加到输出中
-
D: kd(errnow−errlast)
就是 kd 乘以此次误差减上次误差,如果只有 P+D,那相当于是一个弹簧系统,阻尼。当变化越剧烈D的效果就会比较大。可以用来抑制系统过冲,更好的控制在理论值范围内,但是kd过大会导致系统产生一些不必要的震荡,所以可以在系统输出保持平稳的条件下,尽可能地增大kd
1
2
3
4
5
6
7
8
9
10
| float compute(PID* pid, float real) {
pid->err = pid->target - real;
pid->errsum += pid->err;
limitInRange(&pid->errsum, 2000);
pid->err_dif = pid->err - pid->err_last;
pid->err_last = pid->err;
pid->output = pid->kp*pid->err + pid->ki*pid->err_sum + pid->kd*pid->err_dif;
limitInRange(&pid->output, pid->limit);
return pid->output;
}
|
速度控制环一般使用PI控制
位置式PID
输出的结果可以直接作为一个控制量,但是有时候需要加一个前馈。因为有误差积分 ∑ei,一直累加,也就是当前的输出u(k)与过去的所有状态都有关系,用到了误差的累加值;(误差 ei 会有误差累加),输出的u(k)对应的是执行机构的实际位置,一旦控制输出出错(控制对象的当前的状态值出现问题 ),u(k)的大幅变化会引起系统的大幅变化。
并且位置式PID在积分项达到饱和时,误差仍然会在积分作用下继续累积,一旦误差开始反向变化,系统需要一定时间从饱和区退出,所以在u(k)达到最大和最小时,要停止积分作用,并且要有积分限幅和输出限幅,所以在使用位置式PID时,一般直接使用PD控制
output=kperrnow+kij=0∑kej+kd(errnow−errlast)
1
2
3
4
5
6
7
8
9
| float compute(PID* pid, float input) {
pid->err[0] = pid->target - input;
pid->accErr += pid->err[0];
limitInRange(&pid->accErr, pid->accErrLimit);
pid->output = pid->kp*pid->err[0] + pid->ki*pid->accErr + pid->kd*(pid->err[0] - pid->err[1]);
pid->err[2] = pid->err[1];
pid->err[1] = pid->err[0];
return pid->output;
}
|
增量式PID
输出的结果是控制量的增量,控制量是多次计算不断累积出来的结果,增量式pid实际上要根据每次的改变量与上次的改变量的差值来做为 kp 项,只有运行起来的时候 kp 相才有作用。控制量 output 仅与最近3次的采样值有关,容易通过加权处理获得比较好的控制效果,并且在系统发生问题时,增量式不会严重影响系统的工作。
outputi=kp(errnow−errlast)+ki∗errnow+kd(errnow−2errlast+errlastlast)+outputi−1
1
2
3
4
5
6
7
8
| float compute(PID* pid, float input) {
pid->err[0] = pid->target - input;
pid->output = pid->kp*(pid->err[0] - pid->err[1]) + pid->ki*pid->err[0] + pid->kd*(pid->err[0] - 2*pid->err[1] + pid->err[2]);
pid->err[2] = pid->err[1];
pid->err[1] = pid->err[0];
limitInRange(&pid->output, pid->limit);
return pid->output;
}
|
T形积分PID
跟普通的pid相似,是为了减小积分项所带来的误差和控制的幅度
位置式
output=kperrnow+2ki∑j=0kej+kd(errnow−errlast)
增量式
outputi=kp(errnow−errlast)+2kierrnow+kd(errnow−2errlast+errlastlast)+outputi−1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| float TincCompute(PID* pid, float input) {
pid->err[0] = pid->target - input;
float ierr = (pid->err[0] + pid->err[1]) / 2;
pid->output = pid->kp*(pid->err[0] - pid->err[1]) + pid->ki*ierr + pid->kd*(pid->err[0] - 2*pid->err[1] + pid->err[2]);
pid->err[2] = pid->err[1];
pid->err[1] = pid->err[0];
limitInRange(&pid->output, pid->outputLimit);
return pid->output;
}
float TposCompute(PID* pid, float input) {
pid->err[0] = pid->target - input;
pid->accErr += (pid->err[0] + pid->err[1]) / 2;
limitInRange(&pid->accErr, pid->accErrLimit);
pid->output = pid->kp*pid->err[0] + pid->ki*pid->accErr + pid->kd*(pid->err[0] - pid->err[1]);
pid->err[2] = pid->err[1];
pid->err[1] = pid->err[0];
return pid->output;
}
|
不完全微分PID
微分项有引入高频干扰的风险,但若在控制算法中加入低通滤波器,则可使系统性能得到改善。方法之一就是在PID算法中加入一个一阶低通滤波器。这就是所谓的不完全微分,有两种形式,其结构图如下:
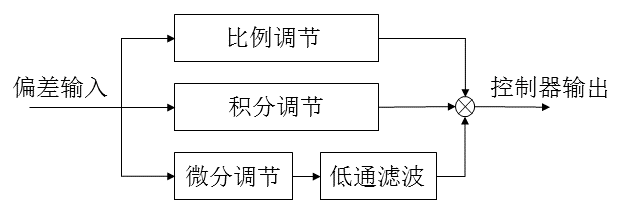
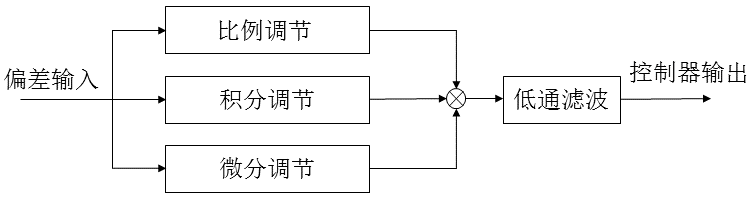
其中微分环节的计算公式为:
-
位置式公式
Ud(k)=kd(1−α)(err(k)−err(k−1))+αUd(k−1)
-
增量式公式:
ΔUd(k)=kd(1−α)(err(k)−err(k−1))−(1−α)Ud(k−1)
或者表示为
ΔUd(k)=kd(1−α)(err(k)−2err(k−1)+err(k−2))+αΔUd(k−1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| typedef struct {
float real;
float target;
float err[3];
float accErr;
float accErrLimit;
float ud;
float deltaud;
float output;
float outputLimit;
float alpha;
float kp;
float ki;
float kd;
}PID;
float posCompute(PID* pid, float input) {
pid->err[0] = pid->target - input;
pid->accErr += pid->err[0];
limitInRange(&pid->accErr, pid->accErrLimit);
pid->ud = pid->kd*(1 - pid->alpha)*(pid->err[0] - pid->err[1]) + pid->alpha*pid->ud;
pid->output = pid->kp*pid->err[0] + pid->ki*pid->accErr + pid->ud;
pid->err[2] = pid->err[1];
pid->err[1] = pid->err[0];
limitInRange(&pid->output, pid->outputLimit);
return pid->output;
}
float incCompute(PID* pid, float input) {
pid->err[0] = pid->target - input;
float deltaud = pid->kd*(1 - pid->alpha)*(pid->err[0] - pid->err[1]) - (1 - pid->alpha)*pid->ud;
pid->ud += deltaud;
pid->output = pid->kp*(pid->err[0] - pid->err[1]) + pid->ki*pid->err[0] + pid->ud;
pid->err[2] = pid->err[1];
pid->err[1] = pid->err[0];
limitInRange(&pid->output, pid->outputLimit);
return pid->output;
}
float incCompute(PID* pid, float input) {
pid->err[0] = pid->target - input;
pid->ud = pid->kd*(1 - pid->alpha)*(pid->err[0] - 2*pid->err[1] + pid->err[2]) + pid->alpha*pid->deltaud;
pid->output = pid->kp*(pid->err[0] - pid->err[1]) + pid->ki*pid->err[0] + pid->ud;
pid->err[2] = pid->err[1];
pid->err[1] = pid->err[0];
limitInRange(&pid->output, pid->outputLimit);
return pid->output;
}
|
微分先行PID
微分先行PID控制是只对输出量进行微分,而对给定指令不起微分作用,因此它适合于给定指令频繁升降的场合,可以避免指令的改变导致超调过大。微分先行的基本结构图:
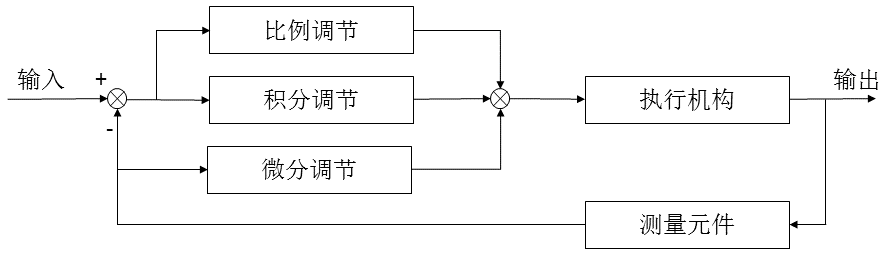
根据上面的结构图,我们可以推出PID控制器的输出公式,比例和积分是不变的只是微分部分变为只对输出对象积分。将输出对象记为 y ,对微分部分引入一阶惯性滤波 γTd+11,则可记微分部分传递函数为 Y(s)Ud(s)=γTds+1Tds+1,于是微分部分公式为 ud(k)=γTd+TγTdud(k−1)+γTd+TTd+Ty(k)+γTd+TTdy(k−1)
由于 kd=kpTTd,带入其中可得
位置式公式
ud(k)=γkd+kpγkdud(k−1)+γkd+kpkd+kpy(k)+γkd+kpkdy(k−1)
增量式公式
Δud(k)=γkd+kpγkdΔud(k−1)+γkd+kpkd+kpΔy(k)+γkd+kpkdΔy(k−1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| typedef struct {
float target;
float err[3];
float input[2];
float deltaInput[2];
float accErr;
float accErrLimit;
float ud;
float deltaud;
float output;
float outputLimit;
float gama;
float kp;
float ki;
float kd;
}PID;
float posCompute(PID* pid, float input) {
pid->input[0] = input;
pid->ud = (pid->gama*pid->kd*pid->ud + (pid->kd + pid->kp)*pid->input[0] + pid->kd*pid->input[1]) / (pid->gama*pid->kd + pid->kp);
pid->input[1] = pid->input[0];
pid->err[0] = pid->target - input;
pid->accErr += pid->err[0];
limitInRange(&pid->accErr, pid->accErrLimit);
pid->output = pid->kp*pid->err[0] + pid->ki*pid->accErr + pid->ud;
limitInRange(&pid->output, pid->outputLimit);
return pid->output;
}
float incCompute(PID* pid, float input) {
pid->input[0] = input;
pid->deltaInput[0] = input - pid->input[1];
pid->deltaud = (pid->gama*pid->kd*pid->deltaud + (pid->kd + pid->kp)*pid->deltaInput[0] + pid->kd*pid->deltaInput[1]) / (pid->gama*pid->kd + pid->kp);
pid->input[1] = pid->input[0];
pid->deltaInput[1] = pid->deltaInput[0];
pid->err[0] = pid->target - input;
pid->output = pid->kp*(pid->err[0] - pid->err[1]) + pid->ki*pid->err[0] + pid->deltaud;
limitInRange(&pid->output, pid->outputLimit);
return pid->output;
}
|
积分分离PID
在过程的启动、结束或大幅度增减设定值时,短时间内系统输出有很大偏差,会造成PID运算的积分累积,引起超调或者振荡。为了解决这一干扰,人们引入了积分分离的思想。其思路是偏差值较大时,取消积分作用,以免于超调量增大;而偏差值较小时,引入积分作用,用来消除静差,提高控制精度。
根据实际情况,设定一个阈值;当偏差大于阈值时,消除积分项仅用PD控制;当偏差小于等于阈值时,引入积分采用PID控制。
位置式
u(k)=⎩⎪⎪⎪⎨⎪⎪⎪⎧kperr(k)+kij=0∑kerr(j)+kd(err(k)−err(k−1))kperr(k)+kd(err(k)−err(k−1))∣err(k)∣≤ε∣err(k)∣>ε
增量式
Δu(k)={kp(err(k)−err(k−1))+kierr(k)+kd(err(k)−2err(k−1)+err(k−2))kp(err(k)−err(k−1))+kd(err(k)−2err(k−1)+err(k−2))∣err(k)∣≤ε∣err(k)∣>ε
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| typedef struct {
float target;
float err[3];
float accErr;
float accErrLimit;
float output;
float outputLimit;
float inputThreshold;
float kp;
float ki;
float kd;
}PID;
float posCompute(PID* pid, float input) {
pid->err[0] = pid->target - input;
pid->accErr += pid->err[0];
limitInRange(&pid->accErr, pid->accErrLimit);
int kicontrol = 1;
if(abs(pid->err[0]) > pid->inputThreshold) kicontrol = 0;
pid->output = pid->kp*pid->err[0] + kicontrol*pid->ki*pid->accErr + pid->kd*(pid->err[0] - pid->err[1]);
pid->err[2] = pid->err[1];
pid->err[1] = pid->err[0];
limitInRange(&pid->output, pid->outputLimit);
return pid->output;
}
float incCompute(PID* pid, float input) {
pid->err[0] = pid->target - input;
int kicontrol = 1;
if(abs(pid->err[0]) > pid->inputThreshold) kicontrol = 0;
pid->output = pid->kp*(pid->err[0] - pid->err[1]) + kicontrol*pid->ki*pid->err[0] + pid->kd*(pid->err[0] - 2*pid->err[1] + pid->err[2]);
pid->err[2] = pid->err[1];
pid->err[1] = pid->err[0];
limitInRange(&pid->output, pid->outputLimit);
return pid->output;
}
|
变速积分PID
在普通的PID控制算法中,由于积分系数ki;是常数,所以在整个控制过程中,积分增量不变。而系统对积分项的要求是,系统偏差大时积分作用应减弱甚至全无,而在偏差小时则应加强。积分系数取大了会产生超调,甚至积分饱和,取小了又迟迟不能消除静差。变速积分PID的基本思想是设法改变积分项的累加速度,使其与偏差大小相对应:偏差越大,积分越慢,反之则越快。主要是为了防止在偏差过大时积分项产生超调,在越接近的时候就产生积分项来消除静态误差,从而更精确的控制系统
位置式:
ui(k)=ki(∑i=0k−1e(i)+f(e(k))∗e(k))
u(k)=kperr(k)+ui(k)+kd∗(err(k)−err(k−1))
增量式:
Δui(k)=kif(e(k))e(k))
Δu(k)=kp(err(k)−err(k−1))+ui(k)+kd(err(k)−2err(k−1)+err(k−2))
其中 f 函数可设为
f(x)=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧1AA−∣x∣+B0∣x∣≤BB<∣x∣≤A+B∣x∣>A+B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| typedef struct {
float target;
float err[3];
float accErr;
float accErrLimit;
float output;
float outputLimit;
float ui;
float deltaui;
float kp;
float ki;
float kd;
float (*func) (float ex);
}PID;
float posCompute(PID* pid, float input) {
pid->err[0] = pid->target - input;
pid->accErr += pid->err[0];
limitInRange(&pid->accErr, pid->accErrLimit);
pid->ui = pid->ki*(pid->accErr + pid->func(pid->err[0])*pid->err[0]);
pid->output = pid->kp*pid->err[0] + pid->ui + pid->kd*(pid->err[0] - pid->err[1]);
pid->err[2] = pid->err[1];
pid->err[1] = pid->err[0];
limitInRange(&pid->output, pid->outputLimit);
return pid->output;
}
float incCompute(PID* pid, float input) {
pid->err[0] = pid->target - input;
pid->deltaui = pid->kp*pid->func(pid->err[0]);
pid->output = pid->kp*(pid->err[0] - pid->err[1]) + pid->deltaui + pid->kd*(pid->err[0] - 2*pid->err[1] + pid->err[2]);
pid->err[2] = pid->err[1];
pid->err[1] = pid->err[0];
limitInRange(&pid->output, pid->outputLimit);
return pid->output;
}
|
模糊PID
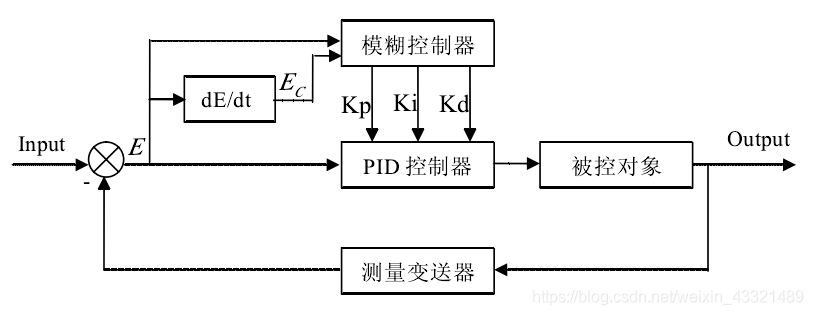
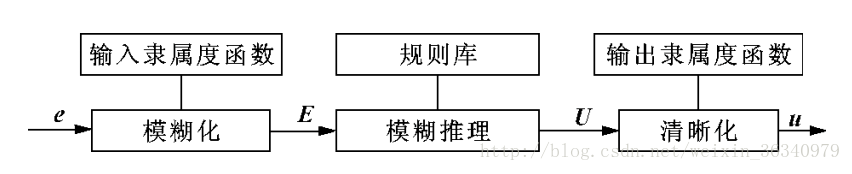
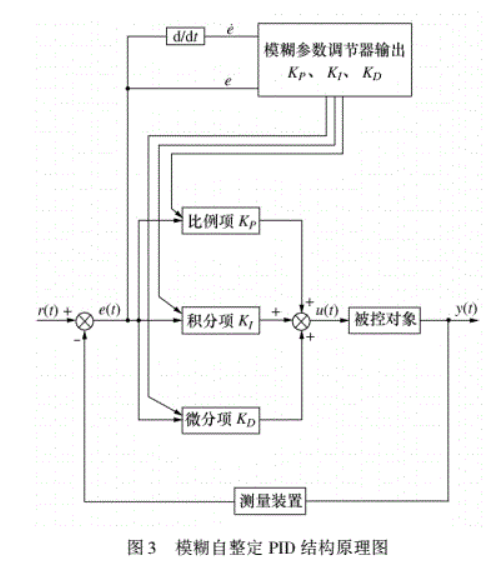
随着自动控制系统被控对象的复杂化,表现为控制系统具有多输入,多输出的强耦合性参数时变性和非线性特性,更突出的问题是从系统获得的信息量相对减少,相反对控制性能得到要求却日益高度化。很多时侯被控对象的精确的数学模型很难或者无法建立。所以可以添加一系列控制规则,再利用模糊理论,模糊语言变量和模糊逻辑推理,将模糊的控制规则上升为数值运算,让计算机实现这些规则,就可以利用计算机模拟人进行自动控制被控对象。
模糊控制系统由模糊数据和规则库,模糊器,模糊推理机和解模糊器组成。并且一般选择 kp,ki,kd 三个系数的增量来作为模糊PID控制的输出值
-
模糊化——模糊器
模糊化相当于是划定一个范围,对于控制对象的偏转值的范围做一个划分。但是偏差值最终目标是0。误差总会在一定范围内波动,一般来说把这个范围划分为6等分。如果误差不在这个范围内,而在 [a,b] 范围内,就可以使用线性差值将这个误差规定在这个范围内
errnow=b−a2errmax(errnow−2a+b)
| NB |
NM |
NS |
ZO |
PS |
PM |
PB |
| −errmax |
−32errmax |
−31errmax |
0 |
31errmax |
32errmax |
errmax |
- N 代表 negative
- P 代表 positive
- B big大
- M middle
- S small
- errmax 偏差的最大范围
隶属度
假设此时的误差为 −41errmax 那么它相对于 NM 的距离为 121errmax,相对于 NS 的距离为 41errmax,那么对于 PB 的隶属度为 121/31=41,相对于 Z0 的隶属度就是 41/31=121
于是隶属度曲线关系为
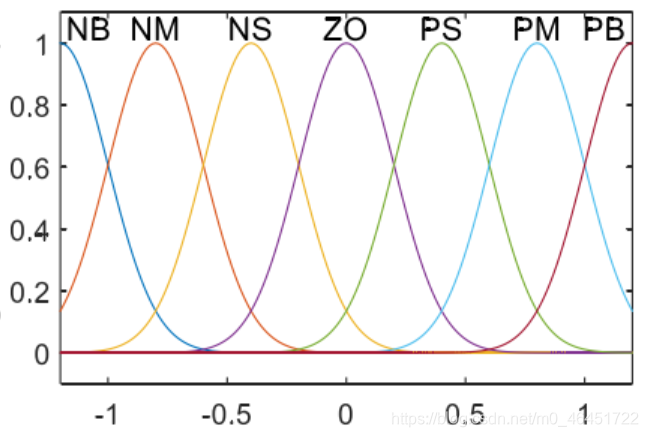
其中利用的是高斯曲线最为隶属度函数的
f(x,σ,c)=e−2σ2(x−c)2
还可以使用三角形,梯形,S型和Z型作为隶属度曲线。实际上这个影响并不大,而每个模糊子集对整个区域的覆盖范围的大小对性能影响较大,一般来说每个模糊子集的宽度如果选择适当,控制效果就会比较好,如果选择宽度较小,则部分区域没有规则相适应,那么收敛性就不好。
对于误差变化率也可以进行模糊化,规则有两种 Mamdini 和 T-S型模糊控制器
-
Mamdini 型模糊控制器
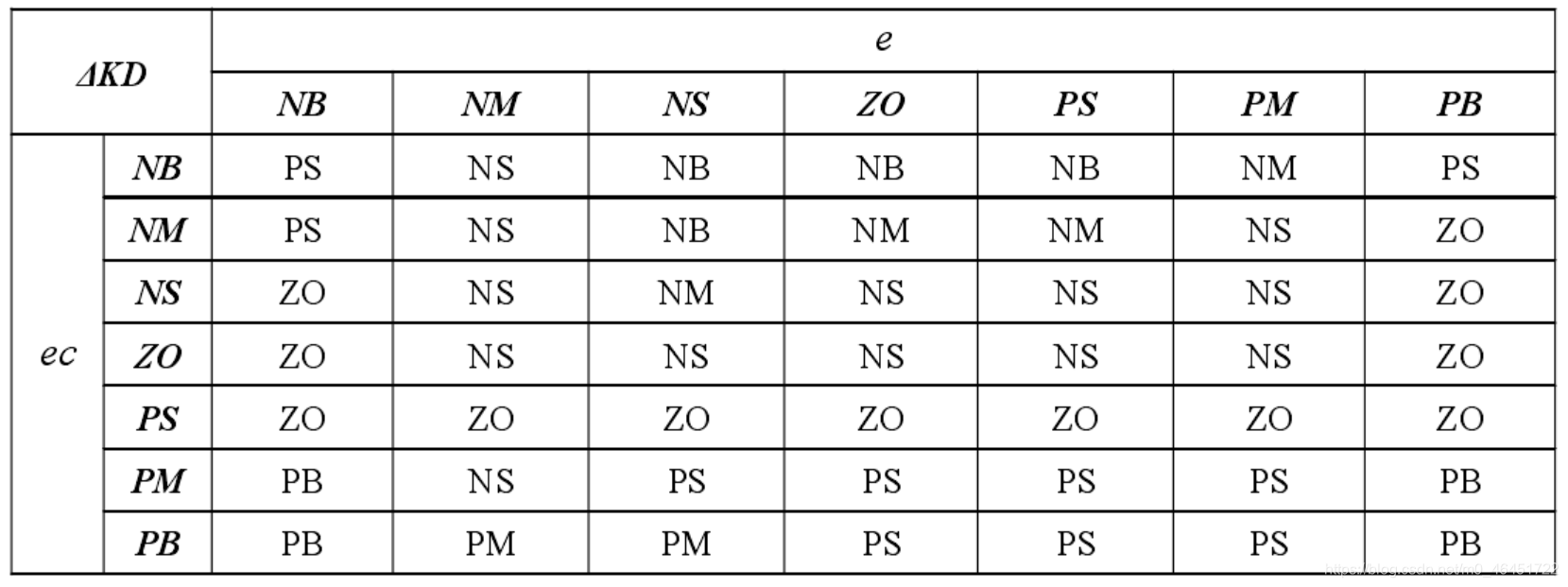
这里的误差变化率为 ec,误差为 e。
在PID中的一般经验是
- 偏差较大时,选用较大的 kp 和较小的 kd 来加快响应,以 kd 为0时来避免积分饱和
- 当偏差很小时,为了消除稳态误差,克服超调,ki 要稍微加大,而 kd 需要取正值,来做一些抑制
-
T-S型模糊控制器
-
模糊推理——模糊推理机
-
去模糊化——解模糊器
对于实际的PID控制需要精确值来做控制,所以需要去模糊化
在实际控制中,每个输入值都会介于两个论阈之间,所以会在规则表中选中一个四格子的矩阵
例子:
假设输入值位于 NM 和 NS 之间,并且输入值的变化量位于 PS 和 PM 之间,则
- E 对于 NM 隶属度为 a,对于 NS 的隶属度为 1-a
- EC 对于 PS 的隶属度为 b,对于 PM 的隶属度为 1-b
所以有多种解模糊化的算法
除此以外还有面积平分法,面积中心法,加权平均法等方法可以使用。
在模糊PID中一般选择 kp,ki,kd 三个值的增量来作为模糊控制的输出值
下面是经验的三个参数的模糊规则
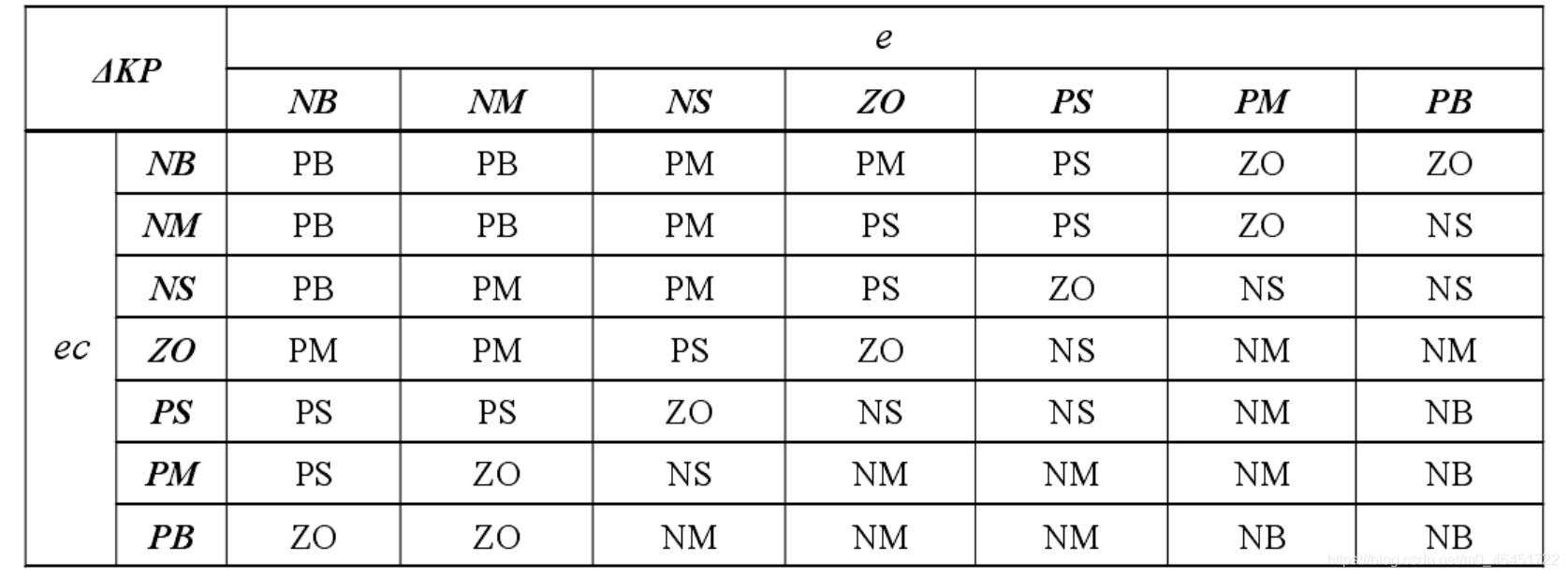
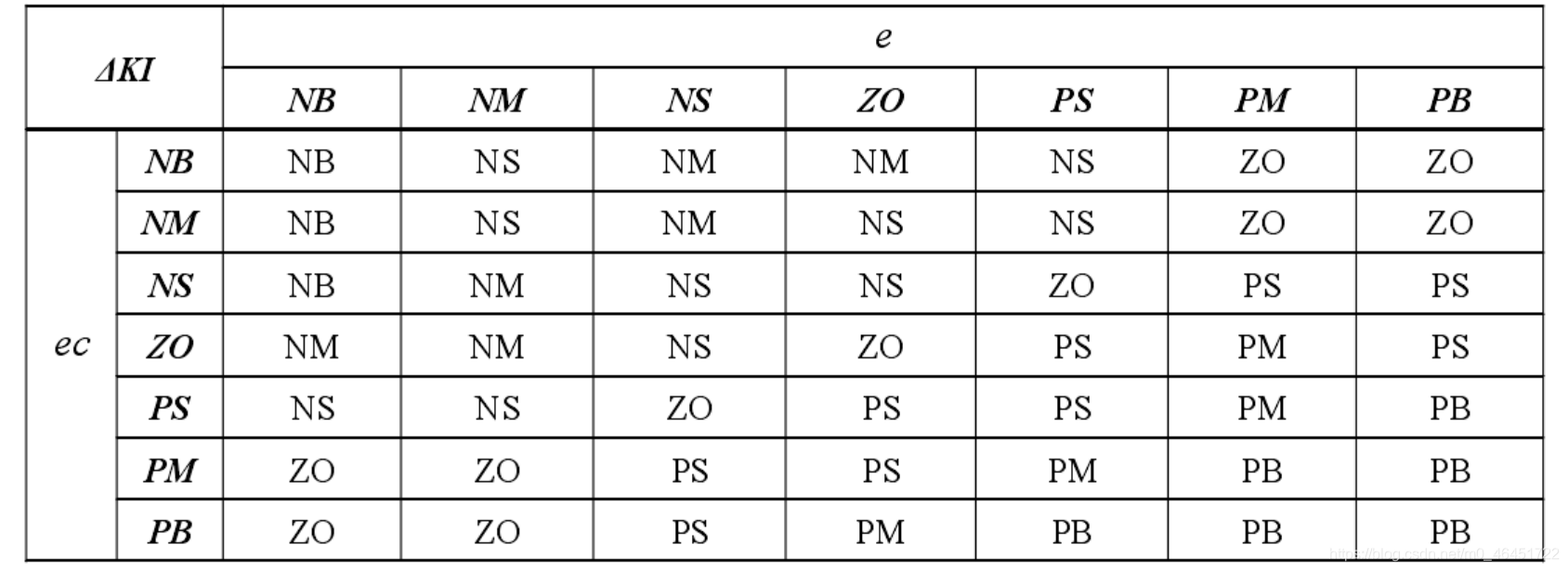
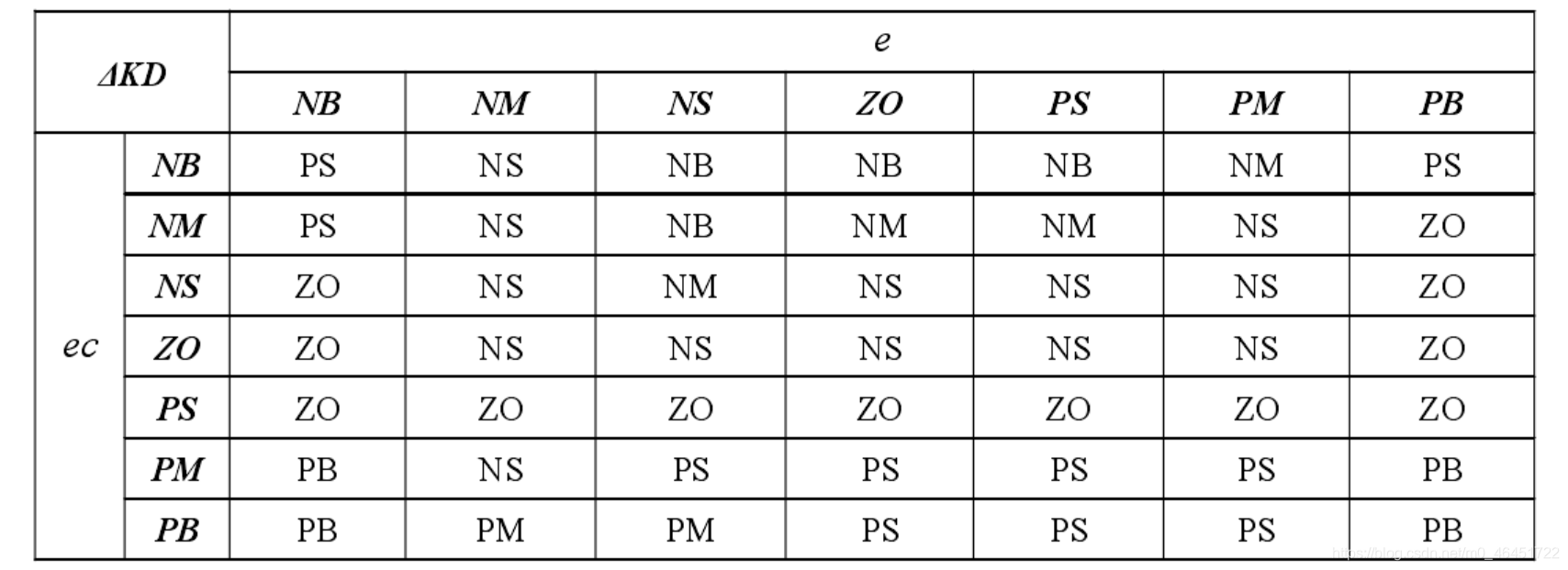
说实话这个傻鸟模糊pid是真难搞,状态量太多了,真是恶心
专家PID
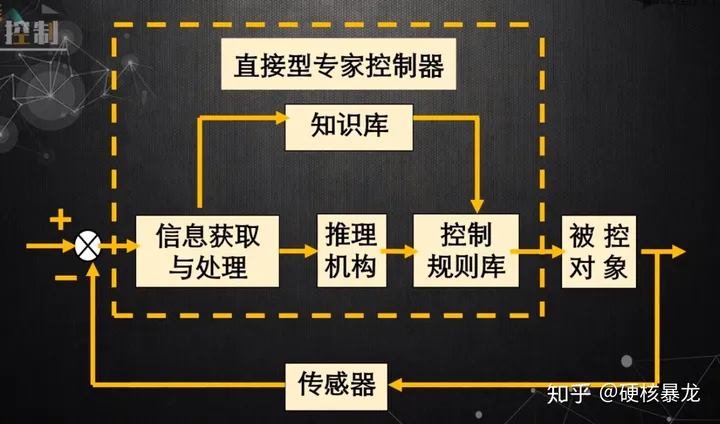
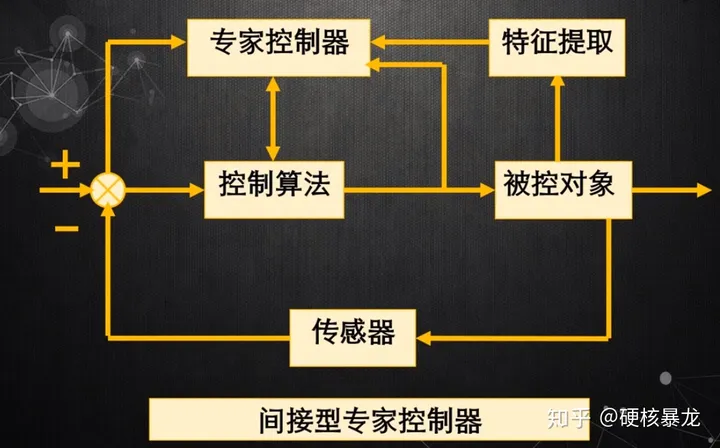
优点:
- 模型的容量大大扩充,通过不断增删修改规则,可以满足任意动态的控制要求,尤其适用于强干扰,时变的,非线性系统的控制,鲁棒性,自适应性很好。
- 可以充分利用先验知识。
- 可以接受定性的描述(可能会需要结合模糊数学的知识)。
- 可以通过故障检测获得更丰富的知识,进行自我的改善和提升。
- 长期连续的可靠性。
控制规则
-
设定误差上限,如果误差值的绝对值已经大于误差上限了,此时直接让控制器满负荷运行
u(k)=sign(err)∗umax
-
设定误差下限,如果误差存在并且误差正在持续不变或者正在变大,可以控制输出值加上一个增量pid的结果值即 u(k)=u(k−1)+k1(kp(err(k)−err(k−1))+ki∗err(k)+kd(err(k)−2err(k−1)+err(k−2)),实际上是把pid的输出值增大
如果误差值大于误差下限,说明误差值仍然较大,可以将 k1 增大,反之可以减小
-
当误差存在并且误差值正在减小,可以将输出维持原值 u(k)=u(k−1)
-
当误差存在并且 Δerr(k)∗Δerr(k−1)<0 说明此时误差值到了极值,此时输出为 u(k)=u(k−1)+k2kie(k),当误差值大于误差下限,说明误差仍然较大,可以适当的将 k2 增大,反之减小
-
设定控制精度,如果误差值在控制精度范围内,就使用 PI 控制,减少稳态误差,此时输出为 u(k)=u(k−1)+kierr(k)+kp(err(k)−err(k−1))
PID的一些缺陷
- 闭环系统动态品质对PID增益的变化很敏感,如果环境变换,PID控制器的参数需要进行调整;
- 基于误差消除误差是PID的精髓,但直接取目标与实际之间的差值并不合理,初始误差大会导致初始控制力大,会使系统出现超调(快速性与超调是相互矛盾的),有时也有控制量饱和的问题;
- 含噪声的信号进行微分难以得到期望的微分信号,PID控制器由于缺少合适的微分器,限制了PID控制的能力;
- PID中的误差积分,有时会让系统的性能变差。
一个比较好用的PID的代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| typedef struct PID {
u8 mode;
float target;
float input;
float err[3];
float accErr;
float pOut;
float iOut;
float dOut;
float output;
float errThreshold;
float integralThreshold;
float kp;
float ki;
float kiScale;
float kd;
} PID;
float PIDCompute(PID* pid, float target, float input) {
pid->err[0] = target - input;
if (fabsf(pid->err[0]) <= pid->errThreshold)
pid->err[0] = 0;
if (fabsf(pid->err[0]) <= pid->integralThreshold)
pid->kiScale = 1;
else
pid->kiScale = 0;
pid->accErr += pid->kiScale*(pid->err[0] + pid->err[1])*0.5f;
switch (pid->mode) {
case PIDPOS:
pid->pOut = pid->kp*pid->err[0];
pid->iOut = pid->ki*pid->accErr*pid->kiScale;
pid->dOut = pid->kd*(pid->err[0] - pid->err[1]);
pid->output = pid->pOut + pid->iOut + pid->dOut;
break;
case PIDINC:
pid->pOut = pid->kp*(pid->err[0] - pid->err[1]);
pid->iOut = pid->ki*pid->kiScale*(pid->err[0] + pid->err[1])*0.5;
pid->dOut = pid->kd*(pid->err[0] - 2*pid->err[1] + pid->err[2]);
pid->output += pid->pOut + pid->iOut + pid->dOut;
break;
}
pid->err[2] = pid->err[1];
pid->err[1] = pid->err[0];
return pid->output;
}
|













