前言
一种典型的不确定系统模型的基本形式是
y = ( P + Δ ) u + n y=(P+\Delta)u+n
y = ( P + Δ ) u + n
其中,y 是系统输出,u 是系统输入,P 是标称对象的传递函数,模型的不确定性以两种形式展现:n 是未知噪声或者干扰, Δ \Delta Δ
一般地说,鲁棒性概念是指反馈控制系统的某项性能对于某集合中的每一个对象都是成立的。具体地说,我们有如下鲁棒性定义。
鲁棒稳定性 :设计一个控制器,使对每一个摄动后的对象,都能保证闭环系统的稳定性。鲁棒性能 :设计一个控制器,使对每一个摄动后的对象,闭环系统都满足稳定性和某种特定的系统性能。
上述鲁棒性的概念是指定给定一个控制器,如果某集合中的每一个对象都能保持某种特性成立,则称控制器对此特性是鲁棒的。因此鲁棒性必须包含一个控制器,有一个对象的集合和某些系统的特性
H ∞ H_\infty H ∞ 一些定义
首先说明一些定义
s u p sup s u p
i n f inf i n f
m a x max m a x
m i n min m i n
I m f Im~f I m f
K e r f Ker~f K e r f f ( x ) = 0 f(x)=0 f ( x ) = 0 K e r f Ker~f K e r f
系统的一些性能指标
IE 增益
Γ i e = s u p w ( t ) = w 0 δ ( t ) , ∥ w 0 ∥ ≤ 1 ∥ z ∥ 2 \Gamma_{ie}=\underset{w(t)=w_0\delta(t),\Vert w_0\Vert\leq1}{sup}\Vert z\Vert_2
Γ i e = w ( t ) = w 0 δ ( t ) , ∥ w 0 ∥ ≤ 1 s u p ∥ z ∥ 2
对于原线性时不变连续时间系统,如果该系统是严格真的(D=0)和渐进稳定(矩阵A特征值均具有负实部)的,那么系统的 IE 增益 是有限的,并且 Γ i e = ∣ ∣ B T Y B ∣ ∣ \Gamma_{ie}=\sqrt{||B^TYB||} Γ i e = ∣ ∣ B T Y B ∣ ∣ max ( e i g ( A T A ) ) \sqrt{\max(eig(A^TA))} max ( e i g ( A T A ) ) e i g eig e i g Y Y Y
Y A + A T Y + C T C = 0 YA+A^TY+C^TC=0
Y A + A T Y + C T C = 0
该定理可以转化为以下的优化问题
m i n γ min~\gamma
m i n γ
其中满足
∃ P : P D P A + A T P + C T C < 0 B T P B ≤ γ I P > 0 \exists P:PD\\\\
PA+A^TP+C^TC<0\\\\
B^TPB\leq\gamma I\\\\
P>0
∃ P : P D P A + A T P + C T C < 0 B T P B ≤ γ I P > 0
该优化问题有一个最优值 γ ⋆ \gamma^\star γ ⋆ Γ i e = γ ⋆ \Gamma_{ie}=\sqrt{\gamma^\star} Γ i e = γ ⋆ LMI 工具箱中的求解器 mincx 来求解
EP 增益
Γ e p = s u p ∣ ∣ w ∣ ∣ 2 ≤ 1 ∣ ∣ z ∣ ∣ ∞ \Gamma_{ep}=\underset{||w||_2\leq1}{sup}||z||_\infty
Γ e p = ∣ ∣ w ∣ ∣ 2 ≤ 1 s u p ∣ ∣ z ∣ ∣ ∞
对于原线性时不变连续时间系统,如果该系统是严格真的(D=0)和渐进稳定(矩阵A特征值均具有负实部)的,那么系统的 EP 增益 是有限的,并且 Γ e p = ∣ ∣ C X C T ∣ ∣ \Gamma_{ep}=\sqrt{||CXC^T||} Γ e p = ∣ ∣ C X C T ∣ ∣ max ( e i g ( A T A ) ) \sqrt{\max(eig(A^TA))} max ( e i g ( A T A ) ) e i g eig e i g X X X
A X + X A T + B T B = 0 AX+XA^T+B^TB=0
A X + X A T + B T B = 0
该定理可以转化为以下的优化问题
m i n γ min~\gamma
m i n γ
其中满足
∃ Q : P D A Q + Q A T + B B T < 0 C Q C T ≤ γ I Q > 0 \exists Q:PD\\\\
AQ+QA^T+BB^T<0\\\\
CQC^T\leq\gamma I\\\\
Q>0
∃ Q : P D A Q + Q A T + B B T < 0 C Q C T ≤ γ I Q > 0
该优化问题有一个最优值 γ ⋆ \gamma^\star γ ⋆ Γ e p = γ ⋆ \Gamma_{ep}=\sqrt{\gamma^\star} Γ e p = γ ⋆ LMI 工具箱中的求解器 mincx 来求解
EE 增益
Γ e e = s u p ∣ ∣ w ∣ ∣ 2 ≤ 1 ∣ ∣ z ∣ ∣ 2 \Gamma_{ee}=\underset{||w||_2\leq1}{sup}||z||_2
Γ e e = ∣ ∣ w ∣ ∣ 2 ≤ 1 s u p ∣ ∣ z ∣ ∣ 2
定理:对于原线性时不变连续时间系统,设 γ \gamma γ
系统渐进稳定,且 Γ e e < γ \Gamma_{ee}<\gamma Γ e e < γ
存在一个对阵阵 P > 0 P>0 P > 0
[ A T P + P A P B C T B T P − γ I D T C D − γ I ] < 0 \begin{bmatrix}A^TP+PA&PB&C^T\\B^TP&-\gamma I&D^T\\C&D&-\gamma I\end{bmatrix}<0
⎣ ⎢ ⎡ A T P + P A B T P C P B − γ I D C T D T − γ I ⎦ ⎥ ⎤ < 0
由于条件 2 是一个线性矩阵不等式,因此可以应用 LMI 工具箱中的求解器 feasp 来判断系统增益 Γ e e \Gamma_{ee} Γ e e
PP 增益
Γ p p = s u p ∣ ∣ w ∣ ∣ ∞ ≤ 1 ∣ ∣ z ∣ ∣ ∞ \Gamma_{pp}=\underset{||w||_\infty\leq1}{sup}||z||_\infty
Γ p p = ∣ ∣ w ∣ ∣ ∞ ≤ 1 s u p ∣ ∣ z ∣ ∣ ∞
定理:对于原线性时不变连续时间系统,设 γ \gamma γ R > 0 R>0 R > 0 γ > 0 \gamma>0 γ > 0 μ > 0 \mu>0 μ > 0
[ A T R + R A + γ R R B B T R − μ I ] < 0 [ γ R 0 C T 0 ( γ − μ ) I D T C D γ I ] > 0 \begin{bmatrix}A^TR+RA+\gamma R&RB\\B^TR&-\mu I\end{bmatrix}<0\\\begin{bmatrix}\gamma R&0&C^T\\0&(\gamma-\mu)I&D^T\\C&D&\gamma^I\end{bmatrix}>0
[ A T R + R A + γ R B T R R B − μ I ] < 0 ⎣ ⎢ ⎡ γ R 0 C 0 ( γ − μ ) I D C T D T γ I ⎦ ⎥ ⎤ > 0
那么满足 Γ p p < γ \Gamma_{pp}<\gamma Γ p p < γ LMI 工具箱中的求解器 feasp 来判断系统增益 Γ e e \Gamma_{ee} Γ e e
LMI矩阵不等式
不确定系统描述
其中有
{ x ˙ = A x + B 1 w + B 2 u z = C 1 x + D 11 w + D 12 u y = C 2 x + D 21 w + D 22 u \left\{\begin{aligned}&\dot{x} = Ax+B_1w+B_2u\\&z = C_1x +D_{11}w+D_{12}u\\&y=C_2x+D_{21}w+D_{22}u\end{aligned}\right.
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ x ˙ = A x + B 1 w + B 2 u z = C 1 x + D 1 1 w + D 1 2 u y = C 2 x + D 2 1 w + D 2 2 u
其中 C 1 , D 11 , D 12 , D 21 , D 22 C_1, D_{11}, D_{12}, D_{21}, D_{22} C 1 , D 1 1 , D 1 2 , D 2 1 , D 2 2
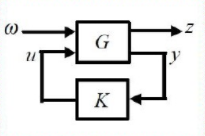
P P P
K K K
u u u
y y y
w w w
z z z
则传递函数为:
U = K Y Y = G 21 W + G 22 U = G 21 W + G 22 K Y Y = ( 1 − G 22 K ) − 1 G 21 W T W Z = Z W = G 11 + G 12 K ( 1 − G 22 K ) − 1 G 21 = F l ( G , K ) U=KY\\\\
Y=G_{21}W+G_{22}U=G_{21}W+G_{22}KY\\\\
Y=(1-G_{22}K)^{-1}G_{21}W\\\\
T_{WZ} = \frac{Z}{W}=G_{11}+G_{12}K(1-G_{22}K)^{-1}G_{21}=F_l(G, K)
U = K Y Y = G 2 1 W + G 2 2 U = G 2 1 W + G 2 2 K Y Y = ( 1 − G 2 2 K ) − 1 G 2 1 W T W Z = W Z = G 1 1 + G 1 2 K ( 1 − G 2 2 K ) − 1 G 2 1 = F l ( G , K )
则有
H ∞ H_{\infty} H ∞
对于标准鲁棒控制器理论控制框图,寻找一个真实有理的控制器 K,使闭环控制系统稳定,而且最小化闭环传递函数矩阵 T Z W T_{ZW} T Z W H ∞ H_{\infty} H ∞
m i n K 镇定 G ∣ ∣ T W Z ( G , K ) ∣ ∣ ∞ \underset {K\text{镇定}G}{min}||T_{WZ}(G, K)||_{\infty}
K 镇定 G min ∣ ∣ T W Z ( G , K ) ∣ ∣ ∞
H ∞ H_{\infty} H ∞
对于标准鲁棒控制器理论控制框图,寻找一个真实有理的控制器 K,使闭环控制系统稳定,而且使闭环传递函数矩阵 T Z W T_{ZW} T Z W H ∞ H_{\infty} H ∞ γ \gamma γ
∣ ∣ T W Z ( G , K ) ∣ ∣ ∞ < γ ||T_{WZ}(G, K)||_{\infty} < \gamma
∣ ∣ T W Z ( G , K ) ∣ ∣ ∞ < γ
Schur 补性质
给定的对称矩阵
S = [ S 11 S 12 S 21 S 22 ] S=\begin{bmatrix}S_{11}&S_{12}\\S_{21}&S_{22}\end{bmatrix}
S = [ S 1 1 S 2 1 S 1 2 S 2 2 ]
其中 S 11 S_{11} S 1 1 r × r r\times r r × r
S < 0,负定
S 11 < 0 , S 22 − S 12 T S 11 − 1 S 12 < 0 S_{11} <0,S_{22}-S_{12}^TS_{11}^{-1}S_{12}<0 S 1 1 < 0 , S 2 2 − S 1 2 T S 1 1 − 1 S 1 2 < 0 S 22 < 0 , S 11 − S 12 S 11 − 1 S 12 T < 0 S_{22} <0,S_{11}-S_{12}S_{11}^{-1}S_{12}^T<0 S 2 2 < 0 , S 1 1 − S 1 2 S 1 1 − 1 S 1 2 T < 0
系统范数
1-范数,信号的时间累计量有界
∥ u ∥ 1 = ∫ − ∞ + ∞ ∣ u ∣ d t \|u\|_1=\int_{-\infty}^{+\infty}|u|dt
∥ u ∥ 1 = ∫ − ∞ + ∞ ∣ u ∣ d t
2-范数,信号的能量有界,平放是对信号能量的一种度量
∥ u ∥ 2 = ∫ − ∞ + ∞ ∣ u ∣ 2 d t \|u\|_2=\sqrt{\int_{-\infty}^{+\infty}|u|^2dt}
∥ u ∥ 2 = ∫ − ∞ + ∞ ∣ u ∣ 2 d t
∞ \infty ∞ ∞ \infty ∞
∥ u ∥ ∞ = e s s s u p t ∈ ( − ∞ , + ∞ ) ∣ u ∣ < ∞ \|u\|_{\infty}=\underset{t\in(-\infty,+\infty)}{ess~sup}|u|<\infty
∥ u ∥ ∞ = t ∈ ( − ∞ , + ∞ ) ess s u p ∣ u ∣ < ∞
sup 表示上确界,ess sup 表示真上确界
系统的 H ∞ H_\infty H ∞ ∣ G ( j w ) ∣ |G(jw)| ∣ G ( j w ) ∣
系统的 H 2 H_2 H 2
Bode 图横坐标: w = 1 0 t , L ( w ) = 20 l g ∣ G ( j w ) ∣ w=10^t, L(w)=20lg|G(jw)| w = 1 0 t , L ( w ) = 2 0 l g ∣ G ( j w ) ∣
状态反馈 H ∞ H_\infty H ∞
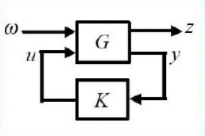
控制问题的基本框图
闭环传递函数确定
考虑线性不变的连续时间系统,存在扰动 w w w
s t a t e : x ˙ = A x + B 1 w + B 2 u z = C 1 x + D 11 w + D 12 u y = C 2 x + D 21 w + D 22 u state:\dot{x}=Ax+B_1w+B_2u\\\\
z=C_1x+D_{11}w+D_{12}u\\\\
y=C_2x+D_{21}w+D_{22}u
s t a t e : x ˙ = A x + B 1 w + B 2 u z = C 1 x + D 1 1 w + D 1 2 u y = C 2 x + D 2 1 w + D 2 2 u
寻找一个控制器 u = K x u=Kx u = K x
x ˙ = A x + B 1 w + B 2 u = ( A + B 2 K ) x + B 1 w z = C 1 x + D 11 w + D 12 u = ( C 1 + D 12 K ) x + D 11 w \dot{x}=Ax+B_1w+B_2u=(A+B_2K)x+B_1w\\\\
z=C_1x+D_{11}w+D_{12}u=(C_1+D_{12}K)x+D_{11}w
x ˙ = A x + B 1 w + B 2 u = ( A + B 2 K ) x + B 1 w z = C 1 x + D 1 1 w + D 1 2 u = ( C 1 + D 1 2 K ) x + D 1 1 w
对于系统 w → z w→z w → z
G ( s ) = C ( s I − A ) − 1 B + D T W Z ( s ) = ( C 1 + D 12 K ) [ s I − ( A + B 2 K ) ] − 1 ] B 1 + D 11 G(s)=C(sI-A)^{-1}B+D\\\\
T_{WZ}(s)=(C_1+D_{12}K)[sI-(A+B_2K)]^{-1}]B_1+D_{11}
G ( s ) = C ( s I − A ) − 1 B + D T W Z ( s ) = ( C 1 + D 1 2 K ) [ s I − ( A + B 2 K ) ] − 1 ] B 1 + D 1 1
状态反馈 H ∞ H_\infty H ∞ 控制器
由于 EE 增益定理,可以得到,给定常数 γ = 1 \gamma=1 γ = 1
[ ( A + B 2 K ) T P + P ( A + B 2 K ) P B 1 ( C 1 + D 12 K ) T B 1 T P − I D 11 T C 1 + D 12 K D 11 − I ] < 0 \begin{bmatrix}(A+B_2K)^TP+P(A+B_2K)&PB_1&(C_1+D_{12}K)^T\\B_1^TP&-I&D_{11}^T\\C_1+D_{12}K&D_{11}&-I\end{bmatrix}<0
⎣ ⎢ ⎡ ( A + B 2 K ) T P + P ( A + B 2 K ) B 1 T P C 1 + D 1 2 K P B 1 − I D 1 1 ( C 1 + D 1 2 K ) T D 1 1 T − I ⎦ ⎥ ⎤ < 0
为了求得未知矩阵 K K K P P P
首先,分别对其左乘和右乘一个对角阵 d i a g { P − 1 , I , I } diag\{P^{-1},I,I\} d i a g { P − 1 , I , I }
[ P − 1 I I ] [ ( A + B 2 K ) T P + P ( A + B 2 K ) P B 1 ( C 1 + D 12 K ) T B 1 T P − I D 11 T C 1 + D 12 K D 11 − I ] [ P − 1 I I ] < 0 ⇓ [ ( A P − 1 + B 2 K P − 1 ) T + ( A P − 1 + B 2 K P − 1 ) B 1 ( C 1 P − 1 + D 12 K P − 1 ) T B 1 T − I D 11 T C 1 P − 1 + D 12 K P − 1 D 11 − I ] < 0 \begin{bmatrix}P^-1\\&I\\&&I\end{bmatrix}\begin{bmatrix}(A+B_2K)^TP+P(A+B_2K)&PB_1&(C_1+D_{12}K)^T\\B_1^TP&-I&D_{11}^T\\C_1+D_{12}K&D_{11}&-I\end{bmatrix}\begin{bmatrix}P^-1\\&I\\&&I\end{bmatrix}<0\\\\\Downarrow\\\\\begin{bmatrix}(AP^{-1}+B_2KP^{-1})^T+(AP^{-1}+B_2KP^{-1})&B_1&(C_1P^{-1}+D_{12}KP^{-1})^T\\B_1^T&-I&D_{11}^T\\C_1P^{-1}+D_{12}KP^{-1}&D_{11}&-I\end{bmatrix}<0
⎣ ⎢ ⎡ P − 1 I I ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ ( A + B 2 K ) T P + P ( A + B 2 K ) B 1 T P C 1 + D 1 2 K P B 1 − I D 1 1 ( C 1 + D 1 2 K ) T D 1 1 T − I ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ P − 1 I I ⎦ ⎥ ⎤ < 0 ⇓ ⎣ ⎢ ⎡ ( A P − 1 + B 2 K P − 1 ) T + ( A P − 1 + B 2 K P − 1 ) B 1 T C 1 P − 1 + D 1 2 K P − 1 B 1 − I D 1 1 ( C 1 P − 1 + D 1 2 K P − 1 ) T D 1 1 T − I ⎦ ⎥ ⎤ < 0
定义 X = P − 1 X=P^{-1} X = P − 1 W = K X W=KX W = K X
[ ( A X + B 2 W ) T + ( A X + B 2 W ) B 1 ( C 1 X + D 12 W ) T B 1 T − I D 11 T C 1 X + D 12 W D 11 − I ] < 0 \begin{bmatrix}(AX+B_2W)^T+(AX+B_2W)&B_1&(C_1X+D_{12}W)^T\\B_1^T&-I&D_{11}^T\\C_1X+D_{12}W&D_{11}&-I\end{bmatrix}<0
⎣ ⎢ ⎡ ( A X + B 2 W ) T + ( A X + B 2 W ) B 1 T C 1 X + D 1 2 W B 1 − I D 1 1 ( C 1 X + D 1 2 W ) T D 1 1 T − I ⎦ ⎥ ⎤ < 0
对于原线性定常系统,存在一个状态反馈 H ∞ H_\infty H ∞ X > 0 X>0 X > 0 X ⋆ X^\star X ⋆ W ⋆ W^\star W ⋆ u = W ⋆ ( X ⋆ ) − 1 x u=W^\star(X^\star)^{-1}x u = W ⋆ ( X ⋆ ) − 1 x H ∞ H_\infty H ∞ X X X W W W LMI 工具箱的求解器 feasp 来求解
状态反馈 γ − \gamma- γ − H ∞ H_\infty H ∞
对于一个给定的标量 γ > 0 \gamma >0 γ > 0 γ − \gamma- γ − H ∞ H_\infty H ∞
∣ ∣ T w z ( s ) ∣ ∣ ∞ < γ ||T_wz(s)||_\infty<\gamma
∣ ∣ T w z ( s ) ∣ ∣ ∞ < γ
可以得到
∣ ∣ γ − 1 T w z ( s ) ∣ ∣ ∞ < 1 ||\gamma^{-1}T_{wz}(s)||_\infty<1
∣ ∣ γ − 1 T w z ( s ) ∣ ∣ ∞ < 1
也就是
∣ ∣ γ − 1 ( C 1 + D 12 K ) [ s I − ( A + B 2 K ) ] − 1 ] B 1 + D 11 ∣ ∣ ∞ < 1 ||\gamma^{-1}(C_1+D_{12}K)[sI-(A+B_2K)]^{-1}]B_1+D_{11}||_\infty<1
∣ ∣ γ − 1 ( C 1 + D 1 2 K ) [ s I − ( A + B 2 K ) ] − 1 ] B 1 + D 1 1 ∣ ∣ ∞ < 1
所以可以通过使用 γ − 1 C 1 , γ − 1 D 12 , γ − 1 D 11 \gamma^{-1}C_1,\gamma^{-1}D_{12},\gamma^{-1}D_{11} γ − 1 C 1 , γ − 1 D 1 2 , γ − 1 D 1 1 C 1 , D 12 , D 11 C_1,D_{12},D_{11} C 1 , D 1 2 , D 1 1
[ ( A X + B 2 W ) T + ( A X + B 2 W ) B 1 γ − 1 ( C 1 X + D 12 W ) T B 1 T − I γ − 1 D 11 T γ − 1 ( C 1 X + D 12 W ) γ − 1 D 11 − I ] < 0 \begin{bmatrix}(AX+B_2W)^T+(AX+B_2W)&B_1&\gamma^{-1}(C_1X+D_{12}W)^T\\B_1^T&-I&\gamma^{-1}D_{11}^T\\\gamma^{-1}(C_1X+D_{12}W)&\gamma^{-1}D_{11}&-I\end{bmatrix}<0
⎣ ⎢ ⎡ ( A X + B 2 W ) T + ( A X + B 2 W ) B 1 T γ − 1 ( C 1 X + D 1 2 W ) B 1 − I γ − 1 D 1 1 γ − 1 ( C 1 X + D 1 2 W ) T γ − 1 D 1 1 T − I ⎦ ⎥ ⎤ < 0
将上式分别左乘和右乘一个对角矩阵 d i a g { I , I , γ I } diag\{I,I,\gamma I\} d i a g { I , I , γ I }
[ ( A X + B 2 W ) T + ( A X + B 2 W ) B 1 ( C 1 X + D 12 W ) T B 1 T − I D 11 T ( C 1 X + D 12 W ) D 11 − γ 2 I ] < 0 \begin{bmatrix}(AX+B_2W)^T+(AX+B_2W)&B_1&(C_1X+D_{12}W)^T\\B_1^T&-I&D_{11}^T\\(C_1X+D_{12}W)&D_{11}&-\gamma^{2}I\end{bmatrix}<0
⎣ ⎢ ⎡ ( A X + B 2 W ) T + ( A X + B 2 W ) B 1 T ( C 1 X + D 1 2 W ) B 1 − I D 1 1 ( C 1 X + D 1 2 W ) T D 1 1 T − γ 2 I ⎦ ⎥ ⎤ < 0
存在一个状态反馈 γ − \gamma- γ − H ∞ H_\infty H ∞ X > 0 X>0 X > 0 X ⋆ X^\star X ⋆ W ⋆ W^\star W ⋆ u = W ⋆ ( X ⋆ ) − 1 x u=W^\star(X^\star)^{-1}x u = W ⋆ ( X ⋆ ) − 1 x H ∞ H_\infty H ∞ X X X W W W LMI 工具箱的求解器 feasp 来求解
状态反馈最优 H ∞ H_\infty H ∞
基于状态反馈 γ − \gamma- γ − H ∞ H_\infty H ∞
min ρ [ ( A X + B 2 W ) T + ( A X + B 2 W ) B 1 ( C 1 X + D 12 W ) T B 1 T − I D 11 T ( C 1 X + D 12 W ) D 11 − ρ I ] < 0 X > 0 \min\rho\\\begin{bmatrix}(AX+B_2W)^T+(AX+B_2W)&B_1&(C_1X+D_{12}W)^T\\B_1^T&-I&D_{11}^T\\(C_1X+D_{12}W)&D_{11}&-\rho I\end{bmatrix}<0\\X>0
min ρ ⎣ ⎢ ⎡ ( A X + B 2 W ) T + ( A X + B 2 W ) B 1 T ( C 1 X + D 1 2 W ) B 1 − I D 1 1 ( C 1 X + D 1 2 W ) T D 1 1 T − ρ I ⎦ ⎥ ⎤ < 0 X > 0
该问题是一个具有线性矩阵不等式约束和线性目标函数的凸优化问题,可以应用LMI工具箱的求解mincx来求解。如果该问题有解,就可以得到系统的状态反馈最优 H ∞ H_\infty H ∞
输出反馈 H ∞ H_\infty H ∞
设计思路
当系统状态难以测量 时,可以选择输出反馈的控制方式,所以就是设计出一个输出反馈控制器 u = K y u=Ky u = K y ∣ ∣ T W Z ( s ) ∣ ∣ ∞ < 1 ||T_{WZ}(s)||_\infty<1 ∣ ∣ T W Z ( s ) ∣ ∣ ∞ < 1
首先需要假定 ( A , B 2 , C 2 ) (A,B_2,C_2) ( A , B 2 , C 2 ) D 22 = 0 D_{22}=0 D 2 2 = 0 u = K y u=Ky u = K y
x ^ ˙ = A K x ^ + B K y u = C K x ^ + D K y \dot{\hat x}=A_K\hat{x}+B_Ky\\\\
u=C_K\hat{x}+D_Ky
x ^ ˙ = A K x ^ + B K y u = C K x ^ + D K y
其中 x ^ \hat{x} x ^ A K , B K , C K , D K A_K,B_K,C_K,D_K A K , B K , C K , D K 待确定的控制器参数矩阵 ,将其带入原系统得到新的广义闭环系统
[ x ˙ x ^ ˙ ] = [ A + B 2 D K C 2 B 2 C K B K C 2 A K ] [ x x ^ ] + [ B 1 + B 2 D K D 21 B K D 21 ] w z = [ C 1 + D 12 D K C 2 D 12 C K ] [ x x ^ ] + ( D 11 + D 12 D K D 21 ) w \begin{bmatrix}\dot{x}\\\dot{\hat x}\end{bmatrix}=\begin{bmatrix}A+B_2D_KC_2&B_2C_K\\B_KC_2&A_K\end{bmatrix}\begin{bmatrix}x\\\hat{x}\end{bmatrix}+\begin{bmatrix}B_1+B_2D_KD_{21}\\B_KD_{21}\end{bmatrix}w\\\\
z=\begin{bmatrix}C_1+D_{12}D_KC_2&D_{12}C_K\end{bmatrix}\begin{bmatrix}x\\\hat{x}\end{bmatrix}+(D_{11}+D_{12}D_KD_{21})w
[ x ˙ x ^ ˙ ] = [ A + B 2 D K C 2 B K C 2 B 2 C K A K ] [ x x ^ ] + [ B 1 + B 2 D K D 2 1 B K D 2 1 ] w z = [ C 1 + D 1 2 D K C 2 D 1 2 C K ] [ x x ^ ] + ( D 1 1 + D 1 2 D K D 2 1 ) w
简化为
x ˙ a = A c x a + B c w z = C c x a + D c w \dot{x}_a=A_cx_a+B_cw\\\\
z=C_cx_a+D_cw
x ˙ a = A c x a + B c w z = C c x a + D c w
由于 EE 增益定理,可以得到,给定常数 γ = 1 \gamma=1 γ = 1 X c X_c X c
[ A c T X c + X c A c X c B c C c B c T X c − I D c T C c D c − I ] < 0 \begin{bmatrix}A_c^TX_c+X_cA_c&X_cB_c&C_c\\B_c^TX_c&-I&D_c^T\\C_c&D_c&-I\end{bmatrix}<0
⎣ ⎢ ⎡ A c T X c + X c A c B c T X c C c X c B c − I D c C c D c T − I ⎦ ⎥ ⎤ < 0
但是可以看到,由于 A c , B c , C c , D c A_c,B_c,C_c,D_c A c , B c , C c , D c 消去法 和变量替代法 。
消元法设计输出反馈 H ∞ H_\infty H ∞ 控制器
定义一个矩阵,这个矩阵将控制器中的待定的参数矩阵集中在一起,这也是输出反馈 H ∞ H_\infty H ∞
设计所需要的输出反馈 H ∞ H_\infty H ∞
求解满足下面定理的矩阵 X 和 Y
求解满足 X − Y − 1 = X 2 X 2 T X-Y^{-1}=X_2X_2^T X − Y − 1 = X 2 X 2 T X 2 ∈ R n × n K X_2\in R^{n\times n_K} X 2 ∈ R n × n K n K n_K n K X − Y − 1 X-Y^{-1} X − Y − 1
用 X X X X 2 X_2 X 2 X c = [ X X 2 T X 2 I ] X_{c}=\begin{bmatrix}X&X_2^T\\X_2&I\end{bmatrix} X c = [ X X 2 X 2 T I ]
将矩阵 X c X_c X c H X c + P X c T K Q + Q T K T P X c < 0 H_{X_c}+P_{X_c}^TKQ+Q^TK^TP_{X_c}<0 H X c + P X c T K Q + Q T K T P X c < 0
其中
A 0 = [ A 0 0 0 ] , B 0 = [ B 1 0 ] , C 0 = [ C 1 0 ] B ‾ = [ 0 B 2 I 0 ] , C ‾ = [ 0 I C 2 0 ] , D ‾ 12 = [ 0 D 12 ] , D ‾ 21 = [ 0 D 21 ] H X c = [ A 0 T X c + X c A 0 X c B 0 C 0 T B 0 T X c − I D 11 T C 0 D 11 − I ] P X c = [ B ‾ T X c 0 D ‾ 12 T ] Q = [ C ‾ D ‾ 21 T 0 ] A_0=\begin{bmatrix}A&0\\0&0\end{bmatrix},B_0=\begin{bmatrix}B_1\\0\end{bmatrix},C_0=\begin{bmatrix}C_1&0\end{bmatrix}\\\overline{B}=\begin{bmatrix}0&B_2\\I&0\end{bmatrix},\overline{C}=\begin{bmatrix}0&I\\C_2&0\end{bmatrix},\overline{D}_{12}=\begin{bmatrix}0&D_{12}\end{bmatrix},\overline{D}_{21}=\begin{bmatrix}0\\D_{21}\end{bmatrix}\\H_{X_c}=\begin{bmatrix}A_0^TX_{c}+X_cA_0&X_cB_0&C_0^T\\B_0^TX_c&-I&D_{11}^T\\C_0&D_{11}&-I\end{bmatrix}\\P_{X_c}=\begin{bmatrix}\overline{B}^TX_c&0&\overline{D}_{12}^T\end{bmatrix}\\Q=\begin{bmatrix}\overline{C}&\overline{D}_{21}^T&0\end{bmatrix}
A 0 = [ A 0 0 0 ] , B 0 = [ B 1 0 ] , C 0 = [ C 1 0 ] B = [ 0 I B 2 0 ] , C = [ 0 C 2 I 0 ] , D 1 2 = [ 0 D 1 2 ] , D 2 1 = [ 0 D 2 1 ] H X c = ⎣ ⎢ ⎡ A 0 T X c + X c A 0 B 0 T X c C 0 X c B 0 − I D 1 1 C 0 T D 1 1 T − I ⎦ ⎥ ⎤ P X c = [ B T X c 0 D 1 2 T ] Q = [ C D 2 1 T 0 ]
定理 :原线性定常系统存在一个输出反馈 H ∞ H_\infty H ∞
1. [ N 0 0 0 I ] T [ A T X + X A X B 1 C 1 T B 1 T X − I D 11 T C 1 D 11 − I ] [ N 0 0 0 I ] < 0 1.~\begin{bmatrix}N_0&0\\0&I\end{bmatrix}^T\begin{bmatrix}A^TX+XA&XB_1&C_1^T\\B_1^TX&-I&D_{11}^T\\C_1&D_{11}&-I\end{bmatrix}\begin{bmatrix}N_0&0\\0&I\end{bmatrix}<0
1 . [ N 0 0 0 I ] T ⎣ ⎢ ⎡ A T X + X A B 1 T X C 1 X B 1 − I D 1 1 C 1 T D 1 1 T − I ⎦ ⎥ ⎤ [ N 0 0 0 I ] < 0
2. [ N c 0 0 I ] T [ A Y + Y A T Y C 1 T B 1 C 1 Y − I D 11 B 1 T C 1 D 11 T − I ] [ N c 0 0 I ] < 0 2.~\begin{bmatrix}N_c&0\\0&I\end{bmatrix}^T\begin{bmatrix}AY+YA^T&YC_1^T&B_1\\C_1Y&- I&D_{11}\\B_1^TC_1&D_{11}^T&- I\end{bmatrix}\begin{bmatrix}N_c&0\\0&I\end{bmatrix}<0
2 . [ N c 0 0 I ] T ⎣ ⎢ ⎡ A Y + Y A T C 1 Y B 1 T C 1 Y C 1 T − I D 1 1 T B 1 D 1 1 − I ⎦ ⎥ ⎤ [ N c 0 0 I ] < 0
3. [ X I I Y ] ≥ 0 3.~\begin{bmatrix}X&I\\I&Y\end{bmatrix}\geq 0
3 . [ X I I Y ] ≥ 0
其中, N 0 , N c N_0,N_c N 0 , N c k e r ( [ C 2 D 21 ] ) ker([C_2~ D_{21}]) k e r ( [ C 2 D 2 1 ] ) k e r ( [ B 2 T D 12 T ] ) ker([B_2^T~ D_{12}^T]) k e r ( [ B 2 T D 1 2 T ] ) I m N o = k e r ( [ C 2 D 21 ] ) ImN_o=ker([C_2~ D_{21}]) I m N o = k e r ( [ C 2 D 2 1 ] ) I m N c = k e r ( [ B 2 T D 12 T ] ) ImN_c=ker([B_2^T~ D_{12}^T]) I m N c = k e r ( [ B 2 T D 1 2 T ] ) N o , N c N_o,N_c N o , N c k e r ( [ C 2 D 21 ] ) ker([C_2~ D_{21}]) k e r ( [ C 2 D 2 1 ] ) k e r ( [ B 2 T D 12 T ] ) ker([B_2^T~ D_{12}^T]) k e r ( [ B 2 T D 1 2 T ] ) 若系统不存在控制输入和测量输出 ,则可以在系统模型中取 B 2 = 0 , C 2 = 0 , D 12 = 0 , D 21 = 0 B_2=0,C_2=0,D_{12}=0,D_{21}=0 B 2 = 0 , C 2 = 0 , D 1 2 = 0 , D 2 1 = 0 N o = I , N c = I N_o=I,N_c=I N o = I , N c = I
1. [ A T X + X A X B 1 C 1 T B 1 T X − I D 11 T C 1 D 11 − I ] < 0 1.~\begin{bmatrix}A^TX+XA&XB_1&C_1^T\\B_1^TX&-I&D_{11}^T\\C_1&D_{11}&-I\end{bmatrix}<0
1 . ⎣ ⎢ ⎡ A T X + X A B 1 T X C 1 X B 1 − I D 1 1 C 1 T D 1 1 T − I ⎦ ⎥ ⎤ < 0
2. [ A Y + Y A T Y C 1 T B 1 C 1 Y − I D 11 B 1 T C 1 D 11 T − I ] < 0 2.~\begin{bmatrix}AY+YA^T&YC_1^T&B_1\\C_1Y&- I&D_{11}\\B_1^TC_1&D_{11}^T&- I\end{bmatrix}<0
2 . ⎣ ⎢ ⎡ A Y + Y A T C 1 Y B 1 T C 1 Y C 1 T − I D 1 1 T B 1 D 1 1 − I ⎦ ⎥ ⎤ < 0
3. [ X I I Y ] ≥ 0 3.~\begin{bmatrix}X&I\\I&Y\end{bmatrix}\geq 0
3 . [ X I I Y ] ≥ 0
相应的上述的设计步骤也会发生改变
其中第四步变为
A 0 = [ A 0 0 0 ] B ‾ = [ 0 B 2 I 0 ] C ‾ = [ 0 I C 2 0 ] H X c = [ A 0 T X c + X c A 0 0 0 0 − I 0 0 0 − I ] P X c = [ B ‾ T X c 0 0 ] Q = [ C ‾ 0 0 ] ⇓ H X c + P X c T K Q + Q T K T P X c < 0 A_0=\begin{bmatrix}A&0\\0&0\end{bmatrix}\\\\
\overline{B}=\begin{bmatrix}0&B_2\\I&0\end{bmatrix}\\\\
\overline{C}=\begin{bmatrix}0&I\\C_2&0\end{bmatrix}\\\\
H_{X_c}=\begin{bmatrix}A_0^TX_{c}+X_cA_0&0&0\\0&-I&0\\0&0&-I\end{bmatrix}\\\\
P_{X_c}=\begin{bmatrix}\overline{B}^TX_c&0&0\end{bmatrix}\\\\
Q=\begin{bmatrix}\overline{C}&0&0\end{bmatrix}\\\\
\Downarrow\\\\
H_{X_c}+P_{X_c}^TKQ+Q^TK^TP_{X_c}<0
A 0 = [ A 0 0 0 ] B = [ 0 I B 2 0 ] C = [ 0 C 2 I 0 ] H X c = ⎣ ⎢ ⎡ A 0 T X c + X c A 0 0 0 0 − I 0 0 0 − I ⎦ ⎥ ⎤ P X c = [ B T X c 0 0 ] Q = [ C 0 0 ] ⇓ H X c + P X c T K Q + Q T K T P X c < 0
控制器 K 便可以获得可以使用 LMI 工具箱的求解器 feasp 来求解
变量替代法设计输出反馈 H ∞ H_\infty H ∞ 控制器
将矩阵 X c X_c X c
X c = [ Y N N T W ] X c − 1 = [ X M M T Z ] X_c=\begin{bmatrix}Y&N\\N^T&W\end{bmatrix}~X_c^{-1}=\begin{bmatrix}X&M\\M^T&Z\end{bmatrix}
X c = [ Y N T N W ] X c − 1 = [ X M T M Z ]
其中, X , Y ∈ R n × n X,Y\in R^{n\times n} X , Y ∈ R n × n X c X c − 1 = I X_cX_c^{-1}=I X c X c − 1 = I
X c [ X M T ] = [ I 0 ] X_c\begin{bmatrix}X\\M^T\end{bmatrix}=\begin{bmatrix}I\\0\end{bmatrix}
X c [ X M T ] = [ I 0 ]
进一步得到
X c [ X I M T 0 ] = [ I Y 0 N T ] X_c\begin{bmatrix}X&I\\M^T&0\end{bmatrix}=\begin{bmatrix}I&Y\\0&N^T\end{bmatrix}
X c [ X M T I 0 ] = [ I 0 Y N T ]
定义
F 1 = [ X I M T 0 ] , F 1 = [ I Y 0 N T ] F_1=\begin{bmatrix}X&I\\M^T&0\end{bmatrix},F_1=\begin{bmatrix}I&Y\\0&N^T\end{bmatrix}
F 1 = [ X M T I 0 ] , F 1 = [ I 0 Y N T ]
也就是 X c F 1 = F 2 X_cF_1=F_2 X c F 1 = F 2
F 1 T X c A c F 1 = F 2 T A c F 1 = [ A X + B 2 ( D K C 2 X + C K M T ) A + B 2 D K C 2 Y ( A + B 2 D K C 2 ) X + N B K C 2 X + Y B 2 C K M T + N A K M T Y A + ( Y B 2 D K + N B K ) C 2 ] F 1 T X c B c = [ B 1 + B 2 D K D 21 Y B 1 + ( Y B 2 D K + N B K ) D 21 ] C c F 1 = [ C 1 X + D 12 ( D K C 2 X + C K M − 1 ) C 1 + D 12 D K C 2 ] F 1 T X c F 1 = F 2 T F 1 = [ X I I Y ] F_1^TX_cA_cF_1=F_2^TA_cF_1\\=\begin{bmatrix}AX+B_2(D_KC_2X+C_KM^T)&A+B_2D_KC_2\\Y(A+B_2D_KC_2)X+NB_KC_2X+YB_2C_KM^T+NA_KM^T&YA+(YB_2D_K+NB_K)C_2\end{bmatrix}\\\\
F_1^TX_cB_c=\begin{bmatrix}B_1+B_2D_KD_{21}\\YB_1+(YB_2D_K+NB_K)D_{21}\end{bmatrix}\\\\
C_cF_1=\begin{bmatrix}C_1X+D_{12}(D_KC_2X+C_KM^{-1})&C_1+D_{12}D_KC_2\end{bmatrix}\\\\
F_1^TX_cF_1=F_2^TF_1=\begin{bmatrix}X&I\\I&Y\end{bmatrix}
F 1 T X c A c F 1 = F 2 T A c F 1 = [ A X + B 2 ( D K C 2 X + C K M T ) Y ( A + B 2 D K C 2 ) X + N B K C 2 X + Y B 2 C K M T + N A K M T A + B 2 D K C 2 Y A + ( Y B 2 D K + N B K ) C 2 ] F 1 T X c B c = [ B 1 + B 2 D K D 2 1 Y B 1 + ( Y B 2 D K + N B K ) D 2 1 ] C c F 1 = [ C 1 X + D 1 2 ( D K C 2 X + C K M − 1 ) C 1 + D 1 2 D K C 2 ] F 1 T X c F 1 = F 2 T F 1 = [ X I I Y ]
为了找到一个适当的变量替换,能够将矩阵不等式非线性的LMI转化为一个等价的线性矩阵不等式。结合以上得到的关系式,定义以下的变量替换公式
A ^ = Y ( A + B 2 D K C 2 ) X + N B K C 2 X + Y B 2 C K M T + N A K M T B ^ = Y B 2 D K + N B K C ^ = D K C 2 X + C K M T D ^ = D K \hat{A}=Y(A+B_2D_KC_2)X+NB_KC_2X+YB_2C_KM^T+NA_KM^T\\\\
\hat{B}=YB_2D_K+NB_K\\\\
\hat{C}=D_KC_2X+C_KM^T\\\\
\hat{D}=D_K
A ^ = Y ( A + B 2 D K C 2 ) X + N B K C 2 X + Y B 2 C K M T + N A K M T B ^ = Y B 2 D K + N B K C ^ = D K C 2 X + C K M T D ^ = D K
可以看到,只要在确定矩阵 M , N M,N M , N
[ A X + X A T + B 2 C ^ + ( B 2 C ^ ) T A ^ T + ( A + B 2 D ^ C 2 ) B 1 + B 2 D ^ D 21 ( C 1 X + D 12 C ^ ) T 0 A T Y + Y A + B ^ C 2 + ( B ^ C 2 ) T Y B 1 + B ^ D 21 ( C 1 + D 12 D ^ C 2 ) T 0 0 − I ( D 11 + D 12 D ^ D 21 ) T 0 0 0 − I ] < 0 \begin{bmatrix}AX+XA^T+B_2\hat{C}+(B_2\hat{C})^T&\hat{A}^T+(A+B_2\hat{D}C_2)&B_1+B_2\hat{D}D_{21}&(C_1X+D_{12}\hat{C})^T\\0&A^TY+YA+\hat{B}C_2+(\hat{B}C_2)^T&YB_1+\hat{B}D_{21}&(C_1+D_{12}\hat{D}C_2)^T\\0&0&-I&(D_{11}+D_{12}\hat{D}D_{21})^T\\0&0&0&-I\end{bmatrix}<0
⎣ ⎢ ⎢ ⎢ ⎡ A X + X A T + B 2 C ^ + ( B 2 C ^ ) T 0 0 0 A ^ T + ( A + B 2 D ^ C 2 ) A T Y + Y A + B ^ C 2 + ( B ^ C 2 ) T 0 0 B 1 + B 2 D ^ D 2 1 Y B 1 + B ^ D 2 1 − I 0 ( C 1 X + D 1 2 C ^ ) T ( C 1 + D 1 2 D ^ C 2 ) T ( D 1 1 + D 1 2 D ^ D 2 1 ) T − I ⎦ ⎥ ⎥ ⎥ ⎤ < 0
现在求出矩阵 M , N M,N M , N
根据恒等式 X c T X c = I X_c^TX_c=I X c T X c = I
M N T = I − X Y MN^T=I-XY
M N T = I − X Y
可以通过矩阵 I − X Y I-XY I − X Y M , N M,N M , N X c > 0 X_c>0 X c > 0
[ X I I Y ] > 0 \begin{bmatrix}X&I\\I&Y\end{bmatrix}>0
[ X I I Y ] > 0
由此可以得到 I − X Y > 0 I-XY>0 I − X Y > 0 M , N M,N M , N
D K = D ^ C K = ( C ^ − D K C 2 X ) ( M T ) − 1 B K = N − 1 ( B ^ − Y B 2 D K ) A K = N − 1 [ A ^ − Y ( A + B 2 D K C 2 ) X ] ( M T ) − 1 − B K C 2 X ( M T ) − 1 − N − 1 Y B 2 C K D_K=\hat{D}\\\\
C_K=(\hat{C}-D_KC_2X)(M^T)^{-1}\\\\
B_K=N^{-1}(\hat{B}-YB_2D_K)\\\\
A_K=N^{-1}[\hat{A}-Y(A+B_2D_KC_2)X](M^T)^{-1}-B_KC_2X(M^T)^{-1}-N^{-1}YB_2C_K
D K = D ^ C K = ( C ^ − D K C 2 X ) ( M T ) − 1 B K = N − 1 ( B ^ − Y B 2 D K ) A K = N − 1 [ A ^ − Y ( A + B 2 D K C 2 ) X ] ( M T ) − 1 − B K C 2 X ( M T ) − 1 − N − 1 Y B 2 C K
所以通过变量替代法将上述非线性 LMI 输出反馈问题转化为如下线性 LMI 问题
[ A X + X A T + B 2 C ^ + ( B 2 C ^ ) T A ^ T + ( A + B 2 D ^ C 2 ) B 1 + B 2 D ^ D 21 ( C 1 X + D 12 C ^ ) T 0 A T Y + Y A + B ^ C 2 + ( B ^ C 2 ) T Y B 1 + B ^ D 21 ( C 1 + D 12 D ^ C 2 ) T 0 0 − I ( D 11 + D 12 D ^ D 21 ) T 0 0 0 − I ] < 0 [ X I I Y ] > 0 M N T = I − X Y \begin{bmatrix}AX+XA^T+B_2\hat{C}+(B_2\hat{C})^T&\hat{A}^T+(A+B_2\hat{D}C_2)&B_1+B_2\hat{D}D_{21}&(C_1X+D_{12}\hat{C})^T\\0&A^TY+YA+\hat{B}C_2+(\hat{B}C_2)^T&YB_1+\hat{B}D_{21}&(C_1+D_{12}\hat{D}C_2)^T\\0&0&-I&(D_{11}+D_{12}\hat{D}D_{21})^T\\0&0&0&-I\end{bmatrix}<0\\\begin{bmatrix}X&I\\I&Y\end{bmatrix}>0\\MN^T=I-XY
⎣ ⎢ ⎢ ⎢ ⎡ A X + X A T + B 2 C ^ + ( B 2 C ^ ) T 0 0 0 A ^ T + ( A + B 2 D ^ C 2 ) A T Y + Y A + B ^ C 2 + ( B ^ C 2 ) T 0 0 B 1 + B 2 D ^ D 2 1 Y B 1 + B ^ D 2 1 − I 0 ( C 1 X + D 1 2 C ^ ) T ( C 1 + D 1 2 D ^ C 2 ) T ( D 1 1 + D 1 2 D ^ D 2 1 ) T − I ⎦ ⎥ ⎥ ⎥ ⎤ < 0 [ X I I Y ] > 0 M N T = I − X Y
可得控制器
D K = D ^ C K = ( C ^ − D K C 2 X ) ( M T ) − 1 B K = N − 1 ( B ^ − Y B 2 D K ) A K = N − 1 [ A ^ − Y ( A + B 2 D K C 2 ) X ] ( M T ) − 1 − B K C 2 X ( M T ) − 1 − N − 1 Y B 2 C K D_K=\hat{D}\\\\
C_K=(\hat{C}-D_KC_2X)(M^T)^{-1}\\\\
B_K=N^{-1}(\hat{B}-YB_2D_K)\\\\
A_K=N^{-1}[\hat{A}-Y(A+B_2D_KC_2)X](M^T)^{-1}-B_KC_2X(M^T)^{-1}-N^{-1}YB_2C_K
D K = D ^ C K = ( C ^ − D K C 2 X ) ( M T ) − 1 B K = N − 1 ( B ^ − Y B 2 D K ) A K = N − 1 [ A ^ − Y ( A + B 2 D K C 2 ) X ] ( M T ) − 1 − B K C 2 X ( M T ) − 1 − N − 1 Y B 2 C K
如上的控制器是状态空间的实行,实际上可以通过 K = pck(Ak,Bk,Ck,Dk)指令得到一个增益的形式,
输出反馈 γ − \gamma- γ − H ∞ H_\infty H ∞
对于一个给定的标量 γ > 0 \gamma>0 γ > 0 γ − \gamma- γ − H ∞ H_\infty H ∞ X , Y X,Y X , Y
1. [ N 0 0 0 I ] T [ A T X + X A X B 1 C 1 T B 1 T X − γ I D 11 T C 1 D 11 − γ I ] [ N 0 0 0 I ] < 0 1.~\begin{bmatrix}N_0&0\\0&I\end{bmatrix}^T\begin{bmatrix}A^TX+XA&XB_1&C_1^T\\B_1^TX&-\gamma I&D_{11}^T\\C_1&D_{11}&-\gamma I\end{bmatrix}\begin{bmatrix}N_0&0\\0&I\end{bmatrix}<0
1 . [ N 0 0 0 I ] T ⎣ ⎢ ⎡ A T X + X A B 1 T X C 1 X B 1 − γ I D 1 1 C 1 T D 1 1 T − γ I ⎦ ⎥ ⎤ [ N 0 0 0 I ] < 0
2. [ N c 0 0 I ] T [ A Y + Y A T Y C 1 T B 1 C 1 Y − γ I D 11 B 1 T C 1 D 11 T − γ I ] [ N c 0 0 I ] < 0 2.~\begin{bmatrix}N_c&0\\0&I\end{bmatrix}^T\begin{bmatrix}AY+YA^T&YC_1^T&B_1\\C_1Y&-\gamma I&D_{11}\\B_1^TC_1&D_{11}^T&-\gamma I\end{bmatrix}\begin{bmatrix}N_c&0\\0&I\end{bmatrix}<0
2 . [ N c 0 0 I ] T ⎣ ⎢ ⎡ A Y + Y A T C 1 Y B 1 T C 1 Y C 1 T − γ I D 1 1 T B 1 D 1 1 − γ I ⎦ ⎥ ⎤ [ N c 0 0 I ] < 0
3. [ X I I Y ] ≥ 0 3.~\begin{bmatrix}X&I\\I&Y\end{bmatrix}\geq 0
3 . [ X I I Y ] ≥ 0
其中, N 0 , N c N_0,N_c N 0 , N c k e r ( [ C 2 D 21 ] ) ker([C_2~D_{21}]) k e r ( [ C 2 D 2 1 ] ) k e r ( [ B 2 T D 12 T ] ) ker([B_2^T~D_{12}^T]) k e r ( [ B 2 T D 1 2 T ] ) LMI 工具箱的求解器 feasp 来求解
输出反馈最优 H ∞ H_\infty H ∞ 控制器
基于输出反馈 γ − \gamma- γ − H ∞ H_\infty H ∞
min ρ [ N 0 0 0 I ] T [ A T X + X A X B 1 C 1 T B 1 T X − ρ I D 11 T C 1 D 11 − ρ I ] [ N 0 0 0 I ] < 0 [ N c 0 0 I ] T [ A Y + Y A T Y C 1 T B 1 C 1 Y − ρ I D 11 B 1 T C 1 D 11 T − ρ I ] [ N c 0 0 I ] < 0 [ X I I Y ] ≥ 0 \min\rho\\\begin{bmatrix}N_0&0\\0&I\end{bmatrix}^T\begin{bmatrix}A^TX+XA&XB_1&C_1^T\\B_1^TX&-\rho I&D_{11}^T\\C_1&D_{11}&-\rho I\end{bmatrix}\begin{bmatrix}N_0&0\\0&I\end{bmatrix}<0\\\begin{bmatrix}N_c&0\\0&I\end{bmatrix}^T\begin{bmatrix}AY+YA^T&YC_1^T&B_1\\C_1Y&-\rho I&D_{11}\\B_1^TC_1&D_{11}^T&-\rho I\end{bmatrix}\begin{bmatrix}N_c&0\\0&I\end{bmatrix}<0\\\begin{bmatrix}X&I\\I&Y\end{bmatrix}\geq 0
min ρ [ N 0 0 0 I ] T ⎣ ⎢ ⎡ A T X + X A B 1 T X C 1 X B 1 − ρ I D 1 1 C 1 T D 1 1 T − ρ I ⎦ ⎥ ⎤ [ N 0 0 0 I ] < 0 [ N c 0 0 I ] T ⎣ ⎢ ⎡ A Y + Y A T C 1 Y B 1 T C 1 Y C 1 T − ρ I D 1 1 T B 1 D 1 1 − ρ I ⎦ ⎥ ⎤ [ N c 0 0 I ] < 0 [ X I I Y ] ≥ 0
该问题是一个具有线性矩阵不等式约束和线性目标函数的凸优化问题,可以应用LMI工具箱的求解mincx来求解。如果该问题有解,就可以得到系统的状态反馈最优 H ∞ H_\infty H ∞
连续时间系统 H ∞ H_\infty H ∞ 控制器综合问题求解器 hinflmi
在 matlab 中可以使用 ltisys 和 hinflmi 函数来求解
1 2 3 4 5 B=[B1 B2];C=[C1;C2];D=[D11,D12;D21,D22]; gamma ;G=ltisys(A,B,C,D); [gopt,K]=hinflmi(G,[1 1 ],gamma ); [Ak,Bk,Ck,Dk]=ltiss(K)
得到满足 H ∞ H_\infty H ∞ γ < g a m m a \gamma<gamma γ < g a m m a H ∞ H_\infty H ∞
hinflmi 函数的基本用法是 [gopt,K]=hinflmi(system,[p m]),通过 mincx 来优化系统的 H ∞ H_\infty H ∞ p 是系统测量输出的个数, m 是系统控制输入的个数, K 是最优 H ∞ H_\infty H ∞ ltiss 函数得到其状态空间实现。
控制器设计
图中的 y 是系统观测量,而 u 是对系统的输入值,K 就是对反馈处理的反馈控制器。要使用两个测量量,即系统加速度和系统的行程,u 是控制系统的加速度来控制系统的,也即这个系统是个二阶系统。当然也可以是一阶系统。对于 w 就是来自于系统外部的输入,例如干扰,噪声和参考信号之类的。对于 z 是一些系统输出的错误信号,可以是真实的也可以是虚拟的,在模型中临时使用来设计控制器, z = [ x x ¨ f ] z=\begin{bmatrix}x\\\ddot{x}\\f\end{bmatrix} z = ⎣ ⎢ ⎡ x x ¨ f ⎦ ⎥ ⎤ H ∞ H_{\infty} H ∞
例子
状态反馈控制
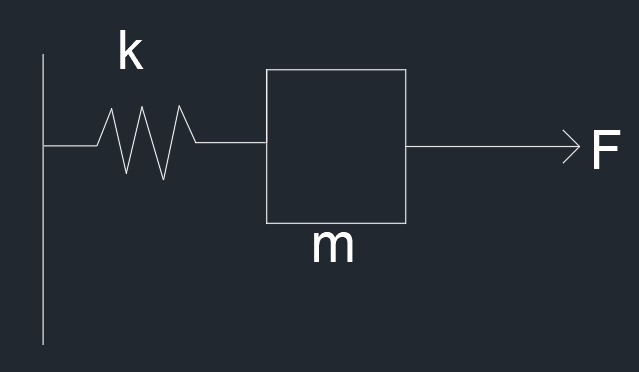
对于一个滑块弹簧系统
可以得到系统状态方程,假设力的最终作用在滑块上存在噪声 w,满足条件,定义噪声 − 0.05 ≤ w ≤ 0.05 , r a n d o m -0.05\leq w\leq 0.05,random − 0 . 0 5 ≤ w ≤ 0 . 0 5 , r a n d o m
[ x 1 ˙ x 2 ˙ ] = [ 0 1 k m 0 ] [ x 1 x 2 ] + [ 0 1 m ] u + [ 1 1 ] w \begin{bmatrix}\dot{x_1}\\\dot{x_2}\end{bmatrix}=\begin{bmatrix}0&1\\\frac{k}{m}&0\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}+\begin{bmatrix}0\\\frac{1}{m}\end{bmatrix}u+\begin{bmatrix}1\\1\end{bmatrix}w
[ x 1 ˙ x 2 ˙ ] = [ 0 m k 1 0 ] [ x 1 x 2 ] + [ 0 m 1 ] u + [ 1 1 ] w
z = [ 1 0 ] [ x 1 x 2 ] y = [ 1 0 ] [ x 1 x 2 ] + [ 0 ] w z=\begin{bmatrix}1&0\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}\\y=\begin{bmatrix}1&0\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}+\begin{bmatrix}0\end{bmatrix}w
z = [ 1 0 ] [ x 1 x 2 ] y = [ 1 0 ] [ x 1 x 2 ] + [ 0 ] w
x ˙ = A x + B 1 w + B 2 u \dot{x}=Ax+B_1w+B_2u
x ˙ = A x + B 1 w + B 2 u
z = C 1 x z=C_1x
z = C 1 x
y = C 2 x + D 21 w y=C_2x+D_{21}w
y = C 2 x + D 2 1 w
将 u = K x u=Kx u = K x
x ˙ = ( A + B 2 K ) x + B 1 w \dot{x}=(A+B_2K)x+B_1w
x ˙ = ( A + B 2 K ) x + B 1 w
z = C 1 x z=C_1x
z = C 1 x
y = C 2 + D 21 w y=C_2+D_{21}w
y = C 2 + D 2 1 w
得到传递函数
T W Z ( s ) = C 1 [ s I − ( A + B 2 K ) ] − 1 B 1 T_{WZ}(s)=C_1[sI-(A+B_2K)]^{-1}B_1
T W Z ( s ) = C 1 [ s I − ( A + B 2 K ) ] − 1 B 1
根据之前的过程可以得到
[ ( A X + B 2 W ) T + ( A X + B 2 W ) B 1 ( C 1 X ) T B 1 T − I 0 C 1 X 0 − I ] < 0 \begin{bmatrix}(AX+B_2W)^T+(AX+B_2W)&B_1&(C_1X)^T\\B_1^T&-I&0\\C_1X&0&-I\end{bmatrix}<0
⎣ ⎢ ⎡ ( A X + B 2 W ) T + ( A X + B 2 W ) B 1 T C 1 X B 1 − I 0 ( C 1 X ) T 0 − I ⎦ ⎥ ⎤ < 0
当且仅当存在一个对称正定矩阵X和矩阵W(W不对称正定),使得上述不等式和 X > 0 X>0 X > 0 u = W ⋆ ( X ⋆ ) − 1 x u=W^\star(X^\star)^{-1}x u = W ⋆ ( X ⋆ ) − 1 x
[ ( A X + B 2 W ) T + ( A X + B 2 W ) B 1 ( C 1 X + D 12 W ) T B 1 T − I D 11 T ( C 1 X + D 12 W ) D 11 − γ 2 I ] < 0 \begin{bmatrix}(AX+B_2W)^T+(AX+B_2W)&B_1&(C_1X+D_{12}W)^T\\B_1^T&-I&D_{11}^T\\(C_1X+D_{12}W)&D_{11}&-\gamma^{2}I\end{bmatrix}<0
⎣ ⎢ ⎡ ( A X + B 2 W ) T + ( A X + B 2 W ) B 1 T ( C 1 X + D 1 2 W ) B 1 − I D 1 1 ( C 1 X + D 1 2 W ) T D 1 1 T − γ 2 I ⎦ ⎥ ⎤ < 0
系统次优 H ∞ H_\infty H ∞
min ρ [ ( A X + B 2 W ) T + ( A X + B 2 W ) B 1 ( C 1 X + D 12 W ) T B 1 T − I D 11 T ( C 1 X + D 12 W ) D 11 − ρ I ] < 0 X > 0 \min\rho\\\begin{bmatrix}(AX+B_2W)^T+(AX+B_2W)&B_1&(C_1X+D_{12}W)^T\\B_1^T&-I&D_{11}^T\\(C_1X+D_{12}W)&D_{11}&-\rho I\end{bmatrix}<0\\X>0
min ρ ⎣ ⎢ ⎡ ( A X + B 2 W ) T + ( A X + B 2 W ) B 1 T ( C 1 X + D 1 2 W ) B 1 − I D 1 1 ( C 1 X + D 1 2 W ) T D 1 1 T − ρ I ⎦ ⎥ ⎤ < 0 X > 0
系统最优 H ∞ H_\infty H ∞
设定 k = 1 , m = 1 k=1,m=1 k = 1 , m = 1
参考文章
鲁棒控制-线性矩阵不等式处理方法——俞立
H∞(H无穷)滤波器(H-infinity filter)
H无穷控制学习笔记——H无穷控制-CSDN博客
H∞输出反馈控制器推导(最后含例子及程序)_h无穷控制器-CSDN博客
持续更新中…